242 |
Беседа 11. Теоремы |
является ромбом, то его диагонали перпендикулярны. Кратко эту тео- рему выражают так (пренебрегая разъяснительной частью): диагонали ромба перпендикулярны.
Однако при формулировании обратной и противоположной тео- рем именно форма записи оказывается весьма существенной. По от-
ношению к (22) обратной является теорема (> x M) (Q(x) P(x)), т. е. если диагонали четырехугольника перпендикулярны, то он явля- ется ромбом. Эта теорема неверна (рис. 342). По отношению к (23) обратной является теорема (> x П) (Q(x) P(x)), т. е. если диаго- нали параллелограмма перпендикулярны, то он является ромбом. Эта теорема верна, в отличие от предыдущей!
Иначе говоря, теорема (23) содержит фактически необходимое и достаточное условие: (> x П) (Q(x) P(x)), т. е. параллелограмм в том и только в том случае является ромбом, если его диагонали перпендикулярны.
Задачи и упражнения
226. Является ли теорема, обратная теореме Пифагора, необходимым и достаточным условием прямоугольности треугольника?
227. Для теоремы: «Диагонали ромба перпендикулярны» составьте об- ратную, противоположную и обратную к противоположной теоремы. Какие из них истинны?
228. Для теоремы: «Диагонали прямоугольника равны» составьте обрат- ную, противоположную и обратную к противоположной теоремы. Какие из них истинны?
229. Утверждение: «Если целое число оканчивается на 0, то оно делится на 5». Является оно необходимым, достаточным или необходимым и доста- точным для делимости числа на 5? Составьте к этому утверждению обратное, противоположное и обратное к противоположному. Какие из них истинны?
230. Верно ли утверждение: «Два треугольника конгруэнтны тогда и только тогда, когда две стороны и заключенный между ними угол одного конгруэнтны двум сторонам и соответствующему углу другого»?
56. Конъюнкция и дизъюнкция
Нередко приходится рассматривать случаи, когда одновременно выполняются два каких-либо свойства. Возьмем, например, высказы- вание: существуют равнобедренные прямоугольные треугольники (рис. 348). Это высказывание означает, что существует :ABC, кото- рый одновременно обладает двумя свойствами: угол C прямой и
AC = BC.
В математике одновременное выполнение двух свойств принято называть конъюнкцией этих свойств и обозначать знаком (читается «и»). Таким образом, сформулированное выше высказывание можно записать так: (? :ABC) ((C = 90°) (AC = BC)).
Еще одним примером использования конъюнкции служит опре- деление пересечения множеств. В самом деле, элемент принадлежит пересечению множеств M и P, если он, во-первых, принадлежит мно- жеству M и, во-вторых, принадлежит множеству P:
56. Конъюнкция и дизъюнкция |
243 |
|
|
M I P = {x: (x M) (x P)}. |
(24) |
Здесь фигурные скобки означают слово «множество», а двоеточие можно заменить словосочетанием «для которых» (т. е. двоеточие по- ясняет, какие x следует взять). Словами запись (24) можно прочитать так: пересечение M I P есть множество тех элементов x, которые принадлежат множеству M и множеству P (рис. 349). Союз «и» в
записи (24) выражен знаком конъюнкции .
Из сказанного ясно, что операция конъюнкции определяется таб- лицей истинности
A |
B |
A B |
|
|
|
И |
И |
И |
И |
Л |
Л |
Л |
И |
Л |
Л |
Л |
Л |
т. е. высказывание A B истинно только в том случае, если истинны оба высказывания A, B.
Кроме знака конъюнкции в математике часто используется знак
дизъюнкции (читается «или»). Знак не совсем точно передается союзом «или», которым мы пользуемся в обычной речи. Возьмем, например, фразу «Я уезжаю, но за книгой зайдет моя сестра или брат». Здесь, скорее всего, союз «или» понимается в смысле «либо- либо», т. е. зайдет либо сестра, либо брат; возможность, что они зайдут вместе, не предусматривается. Иначе говоря, в обычной речи союз «или» чаще всего имеет разделительный оттенок. В математике
знак дизъюнкции не имеет разделительного смысла, т. е. если два
свойства соединены знаком , то это значит, что выполняется хотя бы одно из этих свойств, т. е. либо имеет место первое свойство (но не второе), либо имеет место второе свойство (но не первое), либо же (и в этом отличие) имеют место оба свойства одновременно.
Рассмотрим в качестве примера объединение множеств M и P. Имеет место один из трех случаев (см. рис. 350):
1) либо x M, но x P (точка x1);
2)либо x P, но x M (точка x2);
3)либо x M и x P (точка x3).
Рис. 348 |
Рис. 349 |
Рис. 350 |
244 Беседа 11. Теоремы
Запись (x M) (x P) как раз и означает, что имеет место какой-либо из этих трех случаев.
Из сказанного ясно, что операция дизъюнкции определяется таб- лицей истинности
A |
B |
A B |
|
|
|
И |
И |
И |
И |
Л |
И |
Л |
И |
И |
Л |
Л |
Л |
т. е. высказывание A B ложно только в случае, если ложны оба вы-
сказывания A, B. Поэтому M U P = {x: (x M) (x P)}.
Нередко конъюнкция и дизъюнкция применяются при формули- ровке теорем. Вспомним, например, теорему о том, что катет, лежа- щий против угла 30°, равен половине гипотенузы (рис. 351). Более детально, если треугольник является прямоугольным и один из его углов содержит 30°, то длина катета, лежащего против этого угла, равна половине длины гипотенузы:
(> :ABC) (C = 90°) (A = 30°) (BC = 12 AB).
Здесь в формулировке теоремы использована конъюнкция.
Вот еще пример: если произведение двух чисел равно нулю, то хотя бы один из сомножителей равен нулю, т. е.
(> a, b) (ab = 0) ((a = 0) (b = 0)).
Здесь в заключении теоремы используется дизъюнкция. В тех случаях, когда нужно образовать отрицание утверждения, содержа- щего конъюнкцию или дизъюнкцию, можно воспользоваться следу- ющими эквивалентностями:
@ (P Q) (@ P) (@ Q), |
(25) |
@ (P Q) (@ P) (@ Q), |
(26) |
которые справедливы для любых высказываний (или предикатов) P, Q. Соотношение (25) можно пояснить следующим образом: если не- верно, что справедливы оба утверждения P и Q, то это означает, что неверно P или неверно Q.
Например, четырехугольник ABCD называется параллелограм- мом, если каждые две его противоположные стороны параллельны
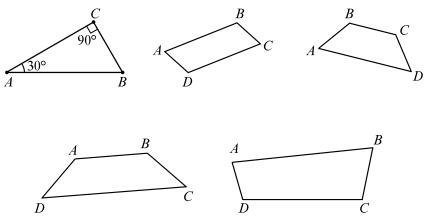
(рис. 352), т. е. (AB || CD) (AD || BC). Если же ABCD не является параллелограммом, т. е. @ ((AB || CD) (AD || BC)), то это означает,
согласно (25), что (@ (AB || CD)) (@ (AD || BC)), т. е. хотя бы одно из условий AB || CD, AD || BC не выполняется. Иными словами, если ABCD — не параллелограмм, то либо не выполняется условие AB || CD (рис. 353), либо не выполняется условие AD || BC (рис. 354), либо же оба эти условия не выполнены (рис. 355).
56. Конъюнкция и дизъюнкция |
245 |
|
|
Рис. 351 |
Рис. 352 |
Рис. 353 |
Рис. 354 |
Рис. 355 |
Рассмотрим еще один иллюстрирующий пример. Будем считать, что вылет самолета состоится в том и только в том случае, если, во-первых, есть горючее и, во-вторых, погода летная. Иначе говоря, необходимое и достаточное условие вылета имеет вид
(есть горючее) (погода летная). Вылет не состоится, если это условие не выполнено, т. е.
@ ((есть горючее) (погода летная)).
Но, согласно (25), это эквивалентно тому, что (@ (есть горючее)) (@ (погода летная)).
Иными словами, вылет не состоится, если нет горючего или погода нелетная.
Разумеется, рассмотрение примеров, подтверждающих разум- ность соотношений (25), (26), не является их доказательством. Уста- новить правильность этих соотношений нетрудно с помощью таблиц истинности. Следующая таблица показывает истинность высказыва-
ний @ (P Q) и (@ P) (@ Q) в зависимости от истинности высказы- ваний P, Q:
P |
Q |
P Q |
@ (P Q) |
@ P |
@ Q |
(@ P) (@ Q) |
|
|
|
|
|
|
|
И |
И |
И |
Л |
Л |
Л |
Л |
И |
Л |
Л |
И |
Л |
И |
И |
Л |
И |
Л |
И |
И |
Л |
И |
Л |
Л |
Л |
И |
И |
И |
И |
Мы видим, что соответствующие столбцы в этих таблицах истин- ности одинаковы, и это показывает, что оба высказывания @ (P Q) и (@ P) (@ Q) эквивалентны, т. е. означают одно и то же. Тем самым
246 Беседа 11. Теоремы
справедливость соотношения (25) подтверждена. Аналогично прове- ряется справедливость соотношения (26).
Выше мы рассматривали в качестве примера определение парал- лелограмма. Знаками его можно записать следующим образом:
(> ABCD) (ABCD — параллелограмм) ≡ ((AB || CD) (AD || BC)). def
Здесь запись (> ABCD) (похожая на разъяснительную часть тео- ремы) показывает, что рассматривается произвольный четырехуголь- ник ABCD. В связи с этим говорят, что «четырехугольник» является родовым понятием (при определении параллелограмма), т. е. рассмат- ривается множество всех четырехугольников и среди них будут выде- ляться те, которые образуют новое понятие (параллелограмм). Далее, запись (ABCD — параллелограмм) представляет собой введение но- вого термина, т. е. мы указываем, как будут называться те четырех-
угольники, которые мы выделяем. Запись ≡ означает, что мы имеем def
дело с определением нового понятия (от английского слова definition). Наконец, запись ((AB || CD) (AD || BC)) указывает видовые отличия, т. е. те отличительные свойства, которыми должен обладать четырех- угольник, чтобы мы считали его параллелограммом.
Словесное определение содержит фактически все эти же части, но не выделенные явно:
четырех- |
называется |
параллело- |
если его противоположные сто- |
угольник |
|
граммом, |
роны попарно параллельны |
↑ |
↑ |
↑ |
↑ |
(родовое |
(def) |
(термин) |
(видовые отличия) |
понятие) |
|
|
|
Для сравнения приведем определение трапеции: оно отличается от определения параллелограмма тем, что при формулировке видо- вых отличий конъюнкция заменяется дизъюнкцией:
(> ABCD) (ABCD — трапеция) ≡ ((AB || CD) (AD || BC)). (27) def
Иными словами, четырехугольник является трапецией, если хотя бы одна пара его противоположных сторон является двумя параллель- ными отрезками. Заметим, что если обе пары противоположных сто- рон параллельны, то четырехугольник также является трапецией (в силу определения дизъюнкции), т. е. параллелограмм — частный слу- чай трапеции. Отметим еще, что многие авторы заменяют это «ди- зъюнктивное» определение другим: четырехугольник называется тра- пецией, если одна пара его противоположных сторон — параллельные отрезки, а другая — нет. Но мы придерживаемся определения (27).
Как мы видим, структура определения очень похожа на структуру теоремы, но части, имеющиеся в записи определения, соединены дру-
56. Конъюнкция и дизъюнкция |
247 |
гим символом (и называются по-другому). При этом теорему надле- жит доказывать, тогда как определение в этом не нуждается.
Заметим еще, что при записи определений рекомендуется исполь- зовать «ближайшее» родовое понятие. Например, определение пря- моугольника можно записать в следующих двух формах:
(> ABCD) (ABCD — прямоугольник) ≡ ( A = B = C = 90°); def
(> пар. ABCD) (ABCD — прямоугольник) ≡ ( A = 90°). def
Первое из этих определений говорит, что произвольный четырех- угольник называется прямоугольником, если у него есть три прямых угла (четвертый угол тогда тоже прямой, так как сумма углов четы- рехугольника равна 360°). Второе определение выделяет прямоуголь- ники из параллелограммов, а не из всех четырехугольников: паралле- лограмм называется прямоугольником, если у него есть один прямой угол (тогда и все углы прямые — в силу свойств параллелограммов). Второе определение использует более близкое к прямоугольнику ро- довое понятие «параллелограмм», чем первое определение.
Рассмотрим следующий пример. Учащемуся предъявляются не- сколько различных фигур: круг, шестиугольник, треугольник, много- угольники, указанные на рис. 352 – 355. Затем предлагается вопрос: какие из этих фигур являются трапециями? Тот, кто уже овладел понятием трапеции, считает, что он «сразу» видит, какие из представ- ленных ему фигур являются трапециями. Однако в действительности
вего сознании идет работа, нередко скрытая от него самого (психо- логи называют такую работу «свернутой», или «автоматизирован- ной»). Если осуществить рефлексию, т. е. «развернуть» эту деятель- ность с помощью психологического самоанализа, то эта деятельность
вее полном виде будет выглядеть следующим образом. Вначале проверяется принадлежность к родовому понятию, т. е. отбрасывает- ся круг (это — не многоугольник), а также шестиугольник и треуголь- ник (это — не четырехугольники). Остаются фигуры, изображенные на рис. 352 – 355. Теперь надо проверить наличие видовых отличий. У фигуры на рис. 355 ни одна пара противоположных сторон не обладает свойством параллельности, значит, это — не трапеция. Ос- таются фигуры на рис. 352 – 354. Они обладают видовыми отличия- ми, т. е. являются трапециями.
Некоторое затруднение может вызвать рис. 352, на котором не одна, а обе пары противоположных сторон являются параллельными. Осознание того, что параллелограмм — частный случай трапеции, весьма важно и связано с пониманием смысла дизъюнкции.
Описанная деятельность вполне соответствует установлению при- надлежности к понятию «трапеция» с помощью определения (27), адекватна этому определению. Аналогичная деятельность адекватна не только определению трапеции, но и многим другим математичес-