
- •Оглавление
- •Предисловие
- •1. Мнения о пользе математики
- •2. Понятия математики и их возникновение
- •3. Некоторые виды абстракции
- •4. Многоступенчатые абстракции
- •6. Количественные отношения реального мира
- •7. Множество и его элементы
- •8. Взаимно однозначное соответствие
- •10. Понятие мощности множества
- •Беседа 3. Операции над множествами
- •11. Пересечение множеств
- •12. Объединение множеств
- •13. Дополнение множеств
- •14. Произведение множеств
- •Беседа 4. Отображения
- •15. Общее понятие отображения и школьная математика
- •16. Некоторые виды отображений
- •17. Обратное отображение
- •18. Композиция отображений
- •19. Классификация
- •Беседа 5. Упорядоченные множества
- •20. Понятие упорядоченного множества
- •21. Минимальные элементы и математическая индукция
- •22. Трансфинитные числа и аксиома выбора
- •Глава 2. Комбинаторика
- •Беседа 6. Размещения, сочетания и родственные задачи
- •23. Размещения с повторениями
- •24. Системы счисления
- •25. Размещения без повторений
- •26. Сочетания без повторений
- •27. Сочетания с повторениями
- •28. Бином Ньютона
- •29. Производящие функции
- •30. Принцип Дирихле
- •Беседа 7. События и вероятности
- •31. События
- •32. Классическое понятие вероятности
- •33. Свойства вероятности
- •34. Условная вероятность
- •35. Независимые события и серии испытаний
- •Беседа 8. Случайные величины
- •37. Нормальное распределение
- •38. Закон больших чисел
- •Беседа 9. Информация
- •40. Количество двоичных цифр
- •41. Задачи на взвешивание
- •42. Понятие об энтропии
- •Беседа 10. Комбинаторные задачи о графах
- •43. Графы и их элементы
- •45. Плоские графы
- •46. Формула Декарта—Эйлера
- •47. Правильные многогранники и паркеты
- •49. Ориентированные графы
- •50. Конечные позиционные игры
- •51. Понятие о сетевом планировании
- •52. Существование и общность
- •53. Структура теоремы
- •54. Отрицание
- •55. Необходимое и достаточное условие
- •56. Конъюнкция и дизъюнкция
- •Беседа 12. Понятие об аксиоматическом методе
- •57. Возникновение аксиоматического метода в математике
- •58. Метрические пространства
- •59. Коммутативные группы
- •Беседа 13. Непротиворечивость, независимость, полнота
- •60. Непротиворечивость и понятие модели
- •61. Математические примеры моделей
- •62. Построение аксиоматики геометрии
- •63. Геометрия Лобачевского
- •64. Модель геометрии Лобачевского
- •65. Изоморфизм моделей
- •66. Полнота аксиоматики
- •67. Цикл озарения
- •68. Сфера достижимости
- •69. Анализ и синтез
- •70. Обратимый анализ
- •72. Поиск решения нестандартных задач
- •Беседа 15. Наглядность. Аналогия. Интуиция
- •74. Формула наглядности — изоморфизм плюс простота
- •75. Наглядность и математическая эстетика
- •76. Аналогия — общность аксиоматики
- •78. Несколько слов о математической интуиции
- •Решения задач и упражнений
- •Предметный указатель

218 |
Беседа 10. Комбинаторные задачи о графах |
и наглядной. Осваивающим программирование можно предложить такое упражнение: «поставить на компьютер» игры, описанные в этой беседе.
Задачи и упражнения
201. Разберите игру в «крестики-нолики» на доске 3×3, при которой каждый играющий может своим ходом поставить как «крестик», так и «нолик». Выигрывает, как обычно, тот, после хода которого на доске оказывается три одинаковых значка, стоящих на одной прямой.
202. Двое играют в такую игру: из кучки, в которой находится 25 спичек, берут по очереди — каждый себе — одну, две или три спички. Выигрывает тот, кто берет последнюю спичку. Кто выигрывает в этой игре — начинаю- щий или его противник?
203. Рассмотрим игру «двойные шахматы», в которой все правила оста- ются прежними, но каждый игрок делает сразу два хода. Докажите, что начинающий не проигрывает при правильной игре.
204. У ромашки n лепестков. Двое по очереди отрывают лепестки. Разрешается отрывать один лепесток или два соседних лепестка. Выигрывает тот, кто оторвет последний лепесток. Кто из играющих может обеспечить себе победу?
205. На окружности расставлено 20 точек, являющихся вершинами пра- вильного двадцатиугольника. За один ход разрешается соединить любые две из них отрезком, не пересекающим (внутри окужности) отрезков, проведен- ных ранее. Проигрывает тот, кто не сможет сделать ход. Кто?
51. Понятие о сетевом планировании
Подготавливается план осуществления некоторого мероприятия, скажем, постройка дачного домика. Вся работа разбивается на от- дельные операции: составление плана, прокладка дороги по участку, подвоз материалов, сооружение фундамента, изготовление бревенча- того сруба, сборка стропил для крыши, настилка пола, установка оконных блоков, внутренняя отделка, установка дверных блоков, кровельные работы, оборудование чердака, установка водоподогре- вателя и отопления, проводка электричества, дымоход, лестница на чердак, запоры на окна и двери. Составленный проект изображается в виде ориентированного графа, вершинами которого служат резуль- таты реализации отдельных операций, а ребра изображают выполнение операций и их зависимость. Для каждой операции определяются пред- шествующие ей операции. Например, установке оконных блоков предшествуют изготовление бревенчатого сруба и настилка полов, тогда как установление оконных блоков и установление дверных блоков не зависят друг от друга (т. е. эти вершины ребром не сое- динены). В результате появляется ориентированный граф («сетевой план», или ПЕРТ), на ребрах которого надписываются планируемые сроки выполнения каждой операции (рис. 323). Этот граф не должен содержать ориентированных циклов (поскольку никакая операция не может предшествовать самой себе), т. е. он устанавливает упорядо- чение в множестве его вершин. Стрелки, представляющие собой след- ствия по транзитивности, не изображаются.

51. Понятие о сетевом планировании |
219 |
На рис. 324 предыдущий граф изображен в виде диаграммы Хассе, в которой вершины располагаются снизу вверх в виде несколь- ких ярусов. Такое изображение графа всегда можно выполнить (воз- можно, с пересечениями ребер). Это позволяет более наглядно пред- ставить зависимость операций друг от друга и их последовательность: например, вершина 4 не может быть достигнута, пока не пройдены вершины 2 и 3.
Для исполнителя проекта особо важную роль играет критический путь, который представляет собой самую неблагоприятную (самую напряженную в смысле времени) ориентированную цепь, ведущую от начальной операции к завершающей, т. е. цепь, которая имеет мак- симальную сумму длительностей операций. На рис. 323, 324 критичес- кий путь вычерчен жирно. Сумма длительностей операций, взятая вдоль критического пути, представляет собой время выполнения про- екта в целом.
Вершины, по которым проходит критический путь, называются критическими операциями. На их выполнение руководитель проекта должен обратить особое внимание, так как любая задержка в выпол- нении какой-либо из этих операций означает задержку завершения всей работы («сдачи объекта»). Напротив, некритические операции допускают некоторое запаздывание в их выполнении (что дает руко- водителю некоторые возможности переброски рабочей силы для под- держки критических операций).
Рассмотренный метод (сетевое планирование) представляет собой важное практическое применение теории графов. Для достаточно слож- ных проектов, содержащих много вершин, нахождение критического пути может представлять собой тру- доемкую задачу, без решения кото- рой однако нельзя обоснованно су- дить о времени возможной реализа- ции проекта. В связи с этим созданы специальные математические алго- ритмы нахождения критического пути. Некоторые из них были разра- ботаны при участии Ричарда Беллма- на, руководителя математического отдела американской корпорации
RAND.
Сказанное выше относится к слу- чаю, когда длительности выполнения операций точно определены (детерми- нированы). На практике же могут иметь место случаи, когда некоторые длительности выполнения операций зависят от случайных обстоятельств
220 |
Беседа 10. Комбинаторные задачи о графах |
|
|
Рис. 325 |
Рис. 326 |
|
(задержка выполнения поставок смежниками из других ведомств, влияние погодных условий и т. п.). В таком случае задача принимает стохастический (вероятностный) характер. Если известно распределе- ние вероятностей для длительности выполнения отдельных операций, то можно вычислить математическое ожидание времени завершения проекта. Обычно распределение вероятностей оценивается (а иногда и корректируется в процессе работы) экспертами (метод экспертных оценок), а вычисления проводятся с помощью компьютеров, т. е. возникают «человеко-машинные» системы сетевого планирования.
Задачи и упражнения
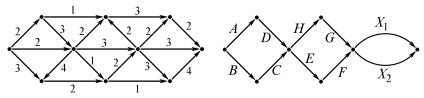
206. Укажите на сетевом графике (рис. 325) критический путь. Чему равно время осуществления проекта?
207. Составьте сетевой график подготовки и проведения шахматного турнира в школе.
208. При проведении ремонта квартиры выполняются следующие опера- ции: а) покупка обоев; б) покупка краски и других малярных материалов; в) шпаклевка потолков и стен; г) принятие решения о ремонте; д) договор с малярами; е) оклеивание стен обоями; ж) окраска дверей и оконных рам; з) побелка потолков; и) шпаклевка дверей и оконных рам.
Составьте сетевой график проведения ремонта квартиры.
209. При компьютерном решении некоторой задачи последовательность вычислений удалось разбить на несколько этапов. При этом каждый этап требует результатов некоторых других этапов и дает данные для проведения некоторых других этапов. На рис. 326 приведен сетевой график процесса решения этой задачи. Для решения задачи задействована сеть из нескольких работающих параллельно компьютеров, результаты вычислений каждого поступают в общую базу данных, но каждый этап вычислений должен выполняться целиком на одном компьютере. Если каждый этап вычислений выполняется в течение 10 секунд машинного времени и в сети достаточно компьютеров, то сколько машинного времени займут вычисления вдоль критического пути? Какое минимальное количество компьютеров будет при этом задействовано?
210. При перестановке мебели в малогабаритной квартире для установки нового шкафа оказалось необходимым произвести следующие операции: а) из прихожей вешалка убирается на кухню; б) шкаф заносится в прихожую; в) из гостиной сервант переносится в спальню; г) на место серванта ставится шкаф; д) вешалка возвращается в прихожую; е) диван переносится на кухню; ж) на место дивана ставится сервант; з) диван переезжает в спальню.
Составьте сетевой график и определите те операции, которые можно выполнить до приезда шкафа.
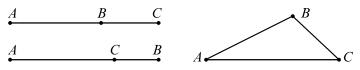
ГЛАВА III. РАССУЖДЕНИЯ Беседа 11. Теоремы
52. Существование и общность
Предложение, о котором можно однозначно установить, истинно оно или ложно, называют высказыванием. Это, конечно, не точное определение, а лишь пояснение. Например, предложения:
A: «3 + 6 = 9»;
B: «Москва — столица России»;
C: «через любые две точки проходит единственная прямая»;
D: «для любых трех точек A, B, C сумма длин отрезков AB и BC не меньше длины отрезка AC» (рис. 327)
являются истинными высказываниями, а предложения: Е: «Париж — столица Италии»;
F: «2×2 = 5»
— ложными высказываниями.
Истинность или ложность некоторого высказывания вовсе не должны быть немедленно очевидными. Например, высказывание C представляет собой в евклидовой геометрии некоторую аксиому, т. е. истинность этого высказывания принимается в этой геометрии без доказательства. А высказывание D представляет собой теорему евк- лидовой геометрии, и истинность этого высказывания устанавлива- ется при помощи некоторого рассуждения (доказательства).
В качестве еще одного примера рассмотрим высказывание
G: «на 1 000 000 000-м месте после запятой в десятичном разло- жении числа π стоит цифра 5».
Мы не можем сказать, истинно это высказывание или ложно, поскольку такого количества цифр числа π сегодня не знает никто. Но принципиально решить этот вопрос можно, т. е. можно узнать, истинно или ложно утверждение G. Например, известно равенство
π4 = 1 − 15 − 17 + 19 − ... и существует точная оценка того, какова величи-
на ошибки, которую мы сделаем, оборвав этот ряд на n-м члене, т. е. принципиально возможно вычислить любую цифру числа π (хотя требуемое для нахождения 1 000 000 000-й цифры этого числа коли- чество вычислений столь велико, что нынешние компьютеры не могут их выполнить в обозримый срок).
А утверждение «Сегодня хорошая погода» высказыванием не будет, даже если уточнить дату, под которой понимается «сегодня», и уточнить в каком именно месте земной поверхности обнаружива-
Рис. 327

222 |
Беседа 11. Теоремы |
ется «хорошая погода». Ведь смысл термина «хорошая погода» одно- значно не определен, и потому вопрос об истинности или ложности высказанного утверждения может не иметь однозначного ответа. Ни- какое вопросительное предложение также не является высказывани- ем. Например, бессмысленно задавать вопрос о том, истинно или
ложно вопросительное предложение «Сколько будет 57 + 168?».
Первое систематическое исследование о высказываниях и опера- циях над ними (о чем мы будем вести разговор ниже) было предпри- нято гениальным древнегреческим ученым Аристотелем, который за- ложил начала логики. Математическое исследование этих вопросов ведет свое начало от основополагающего труда Джорджа Буля, из- данного в Лондоне в 1854 году. Этот труд Буля положил начало математической логики, систематическое развитие которой было до- стигнуто работами многих математиков XX века. Некоторое перво- начальное представление о специфике этой области математики и о ее приложениях (в частности, к школьному курсу математики) мы и предложим читателю в этой главе. А в дальнейших беседах мы не- сколько расширим эти первоначальные представления.
Кроме высказываний в логике рассматриваются предикаты. Пре- дикат — это как бы высказывание, содержащее неизвестную (или несколько неизвестных).
Рассмотрим следующее предложение, содержащее переменную n: «n делится на 7». Обозначим это предложение через A(n). Предложе-
ние A(n) высказыванием не является: о его истинности мы ничего не можем сказать, пока не указано, какое конкретное значение прини- мает п. Например, при n = 1 получается высказывание A(1), которое словами выражается так: «1 делится на 7». Это высказывание ложно. Высказывание же A(14), т. е. «14 делится на 7» — истинно.
Итак, A(n) представляет собой предложение, которое при каждом
конкретном n превращается в некоторое высказывание. Такие пред- ложения в математике называются предикатами. В данном случае
предикат A(n) содержит переменную n, которая может принимать значения из множества натуральных чисел. Поэтому говорят, что предикат A(n) задан на множестве натуральных чисел.
Замечание. Слово «предикат» в переводе с латинского означает «ска- зуемое» (оно употребляется также в немецком, английском и других языках).
Например, рассмотренное выше предложение A(n) содержит в качестве под-
лежащего букву n, а вся остальная часть предложения представляет собой сказуемое «делится» с подчиненными ему словами. Подставляя вместо n то или иное подлежащее (в данном случае числительные 1, 14 и т. д.), мы полу- чаем некоторые высказывания. В дальнейшем в этом пункте высказывания и предикаты мы иногда будем заключать в фигурные скобки.
Аристотель ограничился в своей логике рассмотрением предика- тов только от одной переменной. Но после работ Буля в рассмотрение вошли и предикаты от нескольких переменных. Вот пример предика- та от двух переменных: {Писатель W написал книгу b}. Это пока еще не высказывание, поскольку нам не указано, о каком писателе и о

52. Существование и общность |
223 |
какой книге идет речь. Но если вместо W и b мы подставим какие- либо конкретные значения, получится некоторое высказывание. На- пример, подставив W = Л. Н. Толстой, b = «Война и мир», мы полу- чим истинное высказывание
{Писатель Л. Н. Толстой написал книгу «Война и мир»}.
А при подстановке W = И. С. Тургенев, b = «Анна Каренина» получится ложное высказывание.
Дадим теперь интерпретацию предикатов на языке теории мно- жеств. Рассмотренный выше предикат A(n) задан на множестве N всех натуральных чисел. Множество A N, состоящее из чисел, делящихся на 7: A = {7, 14, 21, 28, 35, 42, 49, ... }, представляет собой множество всех тех значений n, для которых A(n) превращается в истинное
высказывание. Его дополнение cA = N \ A представляет собой множе- ство всех тех значений n, при подстановке которых рассматриваемый предикат превращается в ложное высказывание. Например, 84 A, потому что A(84) — истинное высказывание (число 84 делится на 7), а 37 cA, потому что A(37) — ложное высказывание.
Вообще, если задано некоторое универсальное множество U, на котором определен предикат B(x), то с точки зрения теории множеств это означает, что выделено некоторое подмножество B U, состоя- щее из всех x U, при подстановке которых B(x) превращается в истинное высказывание. Его дополнение cB состоит из всех x U,
при подстановке которых B(x) превращается в ложное высказывание. Это множество B называется множеством истинности предика- та B(x).
Рассмотрим теперь предикаты от двух переменных. Указанный выше предикат о писателях и книгах можно записать так:
L(W, b) = {Писатель W написал книгу b}.
Здесь переменная W пробегает множество A всех писателей, а пере- менная b пробегает множество B всех книг. Каждая пара (W; b) пред-
ставляет собой элемент множества A×B, т. е. произведения множеств
A и B:
B (книги) |
|
|
A (писатели) |
|
|
|
|
Л. Н. Толстой |
И. С. Тур- |
А. С. Пушкин |
И. А. Гончаров |
||
|
|
|
генев |
|
|
|
|
|
|
|
|
|
|
«Война и мир» |
|
z |
z |
|
z |
z |
«Анна Каренина» |
|
z |
z |
|
z |
z |
«Обрыв» |
|
z |
z |
|
z |
z |
«Евгений Онегин» |
|
z |
z |
|
z |
z |
Здесь точками обозначены элементы произведения A×B, т. е. все- возможные пары (W; b), а «галочками» отмечено множество истин-
ности L A × B, т. е. множество тех пар (W; b), при подстановке которых рассматриваемый предикат превращается в истинное выска-
224 |
Беседа 11. Теоремы |
|
|
|
|
зывание. |
Дополнение же A × B \ L состоит из пар, |
при подстановке |
которых получается ложное высказывание. |
|
|
Если |
рассматривается предикат K(a, b, c) от |
трех переменных |
a A, b B, c C, то его множество истинности представляет собой некоторое подмножество K A × B × C.
Множества истинности предикатов нередко обозначают с помо- щью фигурных скобок. Например, запись A = {x N: A(x)} означает,
что A есть множество всех тех x N, для которых имеет место A(x), т. е. множество истинности этого предиката. Более подробно:
A = {x N: x делится на 7}.
В качестве второго примера рассмотрим запись
M = {M R2: AM = BM}.
Она означает множество всех точек M (взятых на плоскости R2), для которых предикат AM = BM превращается в истинное высказыва- ние, т. е. множество всех точек плоскости, равноудаленных от двух заданных точек A и B. Как известно из школьного курса геометрии, это множество представляет собой серединный перпендикуляр к отрез- ку AB.
Вернемся к высказываниям C и D, рассмотренным выше. В них используются выражения «любые две точки», «для любых трех то- чек». Часто приходится формулировать и другие высказывания, в которых используются слова «все», «всякий», «каждый», «любой» и т. п. В математике принято вместо этих слов использовать знак > (перевернутая первая буква A английского слова All — все), который называется знаком общности.
Рассмотрим следующие два утверждения:
(1) сумма величин углов треугольника ABC равна 180°;
(2) в треугольнике ABC угол A прямой.
Чтобы подчеркнуть общность утверждения (1), т. е. его спра- ведливость для любого треугольника ABC, используется знак >:
(> :ABC) ( A + B + C = 180°).
Читается: «для любого треугольника ABC сумма величин углов A, B и C равна 180°». Это — истинное высказывание.
Утверждение (2) такой общностью не обладает. И если перед этим утверждением записать (> :ABC), то получается ложное высказыва- ние. Например, в треугольнике, изображенном на рисунке 328, угол
Aне прямой.
Вкачестве еще одного примера возьмем сформулированное выше
высказывание D. В нем используется предикат AB + BC ≥ AC, в кото- ром имеются три переменные: точки A, B, C. Само же высказывание D можно записать следующим образом:
(> т. A, B, C) (AB + BC ≥ AC).

52. Существование и общность |
225 |
|
|
Рис. 328 Рис. 329
Знак общности в этой записи показывает, что неравенство тре- угольника справедливо для любых точек A, B и C, а обозначение «т.»
— сокращение слова «точка» (в дальнейшем для сокращения слова «прямая» будет применяться обозначение «пр.»).
Вообще, если к некоторому предикату, содержащему, скажем, переменную x, добавить слева запись (> x), т. е. «навесить» на пере- менную x знак общности (или, как говорят математики, квантор общности), то получится некоторое высказывание, истинное или лож- ное.
Возьмем, например, следующий предикат, определенный на мно- жестве H всех людей: A(x) = {x имеет две ноги}.
Навесив на переменную x квантор общности, мы получим выска- зывание (> x H) A(x), т. е. словами: «любой человек x имеет две ноги». Это высказывание, к сожалению, ложно.
Рассмотрим теперь еще один квантор, применяемый в математи- ческой логике — так называемый квантор существования.
Нам часто приходится формулировать высказывания, в которых используются слова: хотя бы один, найдется, существует и т. д. В
математике принято вместо этих слов использовать знак ? (перевер- нутая первая буква E английского слова Exists — «существует»).
Рассмотрим, например, три предиката, заданные на множестве всех треугольников:
A(T ) = {в треугольнике T сумма величин углов равна 180°}; B(T ) = {один из углов треугольника T — прямой};
C(T ) = {два угла треугольника T — прямые}.
Предикат A(T ) для всякого конкретного треугольника T превра- щается в истинное высказывание. Иными словами, высказывание (> T ) A(T ) истинно (в любом треугольнике сумма величин углов равна 180°).
Предикат B(T ) не для всякого конкретного треугольника T пре- вращается в истинное высказывание; например, для треугольника T1 на рис. 329 высказывание B(T1) ложно. Поэтому мы не можем
утверждать, что для любого T имеет место B(T ) — не в любом треугольнике один из углов прямой. Иными словами, высказывание (> T ) B(T ) ложно. Вместе с тем существуют такие треугольники, для которых B(T ) истинно (например, треугольники T2, T3 на рис. 329).
Этот факт записывают с помощью квантора существования ?:
