
- •Оглавление
- •Предисловие
- •1. Мнения о пользе математики
- •2. Понятия математики и их возникновение
- •3. Некоторые виды абстракции
- •4. Многоступенчатые абстракции
- •6. Количественные отношения реального мира
- •7. Множество и его элементы
- •8. Взаимно однозначное соответствие
- •10. Понятие мощности множества
- •Беседа 3. Операции над множествами
- •11. Пересечение множеств
- •12. Объединение множеств
- •13. Дополнение множеств
- •14. Произведение множеств
- •Беседа 4. Отображения
- •15. Общее понятие отображения и школьная математика
- •16. Некоторые виды отображений
- •17. Обратное отображение
- •18. Композиция отображений
- •19. Классификация
- •Беседа 5. Упорядоченные множества
- •20. Понятие упорядоченного множества
- •21. Минимальные элементы и математическая индукция
- •22. Трансфинитные числа и аксиома выбора
- •Глава 2. Комбинаторика
- •Беседа 6. Размещения, сочетания и родственные задачи
- •23. Размещения с повторениями
- •24. Системы счисления
- •25. Размещения без повторений
- •26. Сочетания без повторений
- •27. Сочетания с повторениями
- •28. Бином Ньютона
- •29. Производящие функции
- •30. Принцип Дирихле
- •Беседа 7. События и вероятности
- •31. События
- •32. Классическое понятие вероятности
- •33. Свойства вероятности
- •34. Условная вероятность
- •35. Независимые события и серии испытаний
- •Беседа 8. Случайные величины
- •37. Нормальное распределение
- •38. Закон больших чисел
- •Беседа 9. Информация
- •40. Количество двоичных цифр
- •41. Задачи на взвешивание
- •42. Понятие об энтропии
- •Беседа 10. Комбинаторные задачи о графах
- •43. Графы и их элементы
- •45. Плоские графы
- •46. Формула Декарта—Эйлера
- •47. Правильные многогранники и паркеты
- •49. Ориентированные графы
- •50. Конечные позиционные игры
- •51. Понятие о сетевом планировании
- •52. Существование и общность
- •53. Структура теоремы
- •54. Отрицание
- •55. Необходимое и достаточное условие
- •56. Конъюнкция и дизъюнкция
- •Беседа 12. Понятие об аксиоматическом методе
- •57. Возникновение аксиоматического метода в математике
- •58. Метрические пространства
- •59. Коммутативные группы
- •Беседа 13. Непротиворечивость, независимость, полнота
- •60. Непротиворечивость и понятие модели
- •61. Математические примеры моделей
- •62. Построение аксиоматики геометрии
- •63. Геометрия Лобачевского
- •64. Модель геометрии Лобачевского
- •65. Изоморфизм моделей
- •66. Полнота аксиоматики
- •67. Цикл озарения
- •68. Сфера достижимости
- •69. Анализ и синтез
- •70. Обратимый анализ
- •72. Поиск решения нестандартных задач
- •Беседа 15. Наглядность. Аналогия. Интуиция
- •74. Формула наглядности — изоморфизм плюс простота
- •75. Наглядность и математическая эстетика
- •76. Аналогия — общность аксиоматики
- •78. Несколько слов о математической интуиции
- •Решения задач и упражнений
- •Предметный указатель
43. Графы и их элементы |
185 |
Беседа 10. Комбинаторные задачи о графах
43. Графы и их элементы
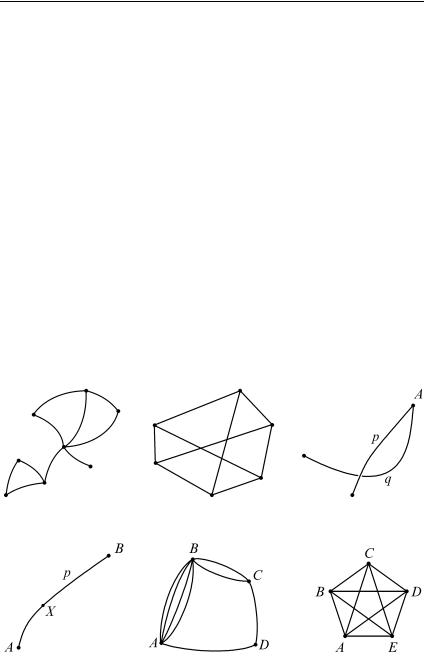
На рис. 233 и других этого пункта изображены некоторые графы. Каждый граф имеет вершины и ребра, причем каждое ребро соединяет какие-либо две вершины. Чаще всего рассматривают графы, у кото- рых множество вершин конечно и множество ребер также конечно. На рисунках вершины изображаются маленькими кружочками, а ребра — соединяющими их дугами (в частности, отрезками).
На рис. 234 граф содержит 6 вершин и 9 ребер, причем некоторые ребра изображены пересекающимися. Однако следует представлять себе, что этих «лишних» точек пересечения как бы не существует. Например, можно считать, что ребра являются некоторыми дугами в пространстве, и лишь за счет изображения графа на плоскости воз- никли эти «лишние» пересечения ребер. Иначе говоря, если p и q — два ребра некоторого графа и A — общая точка этих ребер, то A является концом каждого из этих ребер (рис. 235). Можно дать и иное пояснение: если в некотором графе имеется ребро p с концевыми вершинами A и B (рис. 236), то никакая внутренняя точка X дуги p не является ни вершиной этого графа, ни точкой, принадлежащей какому-либо другому ребру.
В графе, изображенном на рис. 237, вершины A и B соединены четырьмя ребрами, а вершины B и C — двумя. В таком случае говорят, что имеется четырехкратное ребро, соединяющее вершины A и B, и двукратное ребро, соединяющее B и C. Мы условимся в дальнейшем под термином «граф» понимать граф без кратных ребер
Рис. 233 |
Рис. 234 |
Рис. 235 |
|
Рис. 236 |
Рис. 237 |
Рис. 238 |

186 |
Беседа 10. Комбинаторные задачи о графах |
(если не оговорено специально, что допускается рассмотрение крат- ных ребер). Таким образом, если A и B — вершины графа, то либо существует одно ребро, соединяющее эти вершины, либо же вершины A и B ребром не соединены.
Граф с n вершинами, в котором каждые две вершины соединены ребром, называется полным графом с n вершинами. На рис. 238 изо- бражен полный граф с пятью вершинами (напомним, что «лишние» точки пересечения ребер, связанные с изображением этого графа на плоскости, считаются как бы не существующими; например, ребра AC и BD не имеют общих точек в этом графе). Легко видеть, что
полный граф с n вершинами содержит n2 ребер (т. е. ровно столько,
сколько имеется пар вершин). Если же граф с n вершинами не является полным, то его можно получить следующим образом: взять полный граф с этими n вершинами (т. е. каждые две вершины соединить ребром), а затем ненужные ребра удалить. Из этого вытекает, что
любой граф с n вершинами имеет не более n2 ребер.
Пусть, например, проводятся игровые спортивные соревнования
— чемпионат, в котором участвует n команд, причем по условиям чемпионата каждые две команды должны провести между собой одну игру. Будем считать команды вершинами графа, а игру между двумя командами — ребром, содержащим соответствующие вершины. После завершения чемпионата мы получим полный граф с n вершинами, поскольку для любых двух вершин (команд) имеется соединяющее их ребро (игра между этими командами). Всего в течение чемпионата
должно быть проведено n2 игр — по числу ребер полного графа с
n вершинами. Если же мы рассмотрим некоторый момент, когда часть игр уже проведена, но чемпионат еще не закончился, то получим граф с n вершинами, в котором проведены не все ребер, а лишь некоторые из них, соответствующие уже проведенным играм.
В качестве второго примера рассмотрим граф знакомства. Име- ются n персон — будем считать их вершинами графа. Две вершины условимся соединять ребром, если соответствующие персоны знакомы друг с другом (для четкости будем считать, что два человека знакомы, если каждый из них знает другого по имени и хоть раз обменялся с ним рукопожатием). В зависимости от выбора рассматриваемой груп-
пы персон в этом графе может быть от 0 до n2 ребер.
Пусть G — некоторый граф и a — его вершина. Индексом верши- ны a называется число ребер графа G, имеющих a своим концом, т. е. число ребер примыкающих к вершине a (или, как еще говорят, инци- дентных вершине a). Этот индекс мы будем обозначать через ind a
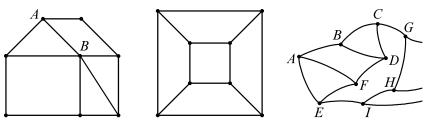
(или, более полно, indG a). Например, на рис. 239 имеем ind A = 3,
ind B = 5. В графах, изображенных на рис. 234 и 240, каждая вершина имеет индекс 3, а в графе на рис. 238 каждая вершина имеет индекс 4.
43. Графы и их элементы |
187 |
|
|
Рис. 239 |
Рис. 240 |
Рис. 241 |
Вообще, в полном графе с n вершинами каждая вершина имеет индекс n − 1.
Следующая несложно доказываемая теорема устанавливает связь между индексами вершин конечного графа и числом его ребер: во всяком конечном графе сумма индексов всех его вершин равна удвоен- ному числу ребер графа. Иначе говоря,
∑ ind a = 2P, |
(1) |
a |
|
где сумма в левой части распространена на все вершины графа, а P
— число его ребер. В самом деле, в сумме, стоящей в левой части равенства (1), каждое ребро засчитывается дважды: с того и с другого конца. Потому эта сумма и равна удвоенному числу ребер.
Из доказанной формулы (1) конечном графе G все вершины справедливо соотношение
вытекает, в частности, что если в имеют один и тот же индекс k, то
Bk = 2P, |
(2) |
где B — число вершин графа G.
В качестве примера рассмотрим следующую комбинаторную за- дачу из довоенного мехматского фольклора Московского универси- тета. Можно ли 77 абонентов соединить телефонными линиями так, чтобы каждый абонент был соединен линиями ровно с тремя другими (на рис. 241 изображен фрагмент такой телефонной сети)? Ответ, как показывает формула (2), отрицательный. Действительно, если бы ис- комый граф (вершинами которого являются абоненты, а ребрами — соединяющие их линии связи) существовал, то в нем каждая вершина имела бы индекс 3, и потому левая часть в (2) была бы равна 77 3, т. е. была бы нечетным числом. Однако это невозможно, поскольку правая часть в (2) четна.
Более общим образом, из формулы (1) вытекает, что в любом конечном графе число вершин, имеющих нечетные индексы, является четным.

188 |
Беседа 10. Комбинаторные задачи о графах |
Задачи и упражнения
166. Семеро коллег послали друг другу поздравительные новогодние открытки, причем каждый послал открытки трем коллегам. Могло ли случиться, что каждый из них получил открытки именно от тех своих коллег, которым он послал поздравления?
167. 30 команд участвуют в первенстве по футболу в один круг (каждые две команды встречаются один раз). Докажите, что в любой момент состя- заний найдутся две команды, сыгравшие одинаковое число матчей.
168. Существует ли граф с пятью вершинами, у которого индексы вершин все различны и равны 0, 1, 2, 3 и 4?
169. Докажите, что в любом графе число вершин с нечетными индексами всегда четно.
170. Пусть в графе с n вершинами только одна пара вершин имеет одинаковые индексы. Докажите, что в этом случае у графа имеется либо
вершина индекса 0 (отдельная вершина), либо вершина индекса n − 1.
44. Цепи и циклы в графах
Последовательность ребер графа называется цепью, если эти ребра можно вычертить одно за другим, не отрывая карандаша и не про- ходя какое-либо ребро дважды. Если ребра p1, p2, ..., pk образуют
цепь, то их концы можно обозначить таким образом: p1 = A0A1, p2 = A1A2, ..., pk = Ak−1Ak, т. е. начало каждого следующего ребра со- впадает с концом предыдущего. Вершины A0 и Ak называются кон- цами цепи A0A1 ... Ak. Если цепь замкнута, т. е. конечная вершина Ak совпадает с начальной вершиной A0, то цепь называется циклом.
Подчеркнем, что никакое ребро не может входить в цепь два или большее число раз. На рис. 242 ребра p1, p2, p3, p4, p2, p5 цепь не
образуют. Ребра p1, p2, p2, p3 на рис. 243 также не образуют цепь. В
то же время цепь может пересекать себя, т. е. дважды (или большее число раз) проходить через некоторые вершины. На рис. 244 цепь
дважды проходит через вершину A2 = A5, т. е. содержит «петлю» A2A3A4A5. Если же цепь A0A1...Ak не пересекает себя, т. е. все верши- ны A0, A1, ..., Ak различны (рис. 245), то цепь называется простой. В частности, цикл без самопересечений называется простым циклом.
Рис. 242 |
Рис. 243 |
Рис. 244 |

44. Цепи и циклы в графах |
189 |
Ясно, что если цепь с концами не является простой, т. е. имеет самопересечения, то можно, выбросив петли, получить простую цепь с теми же концами a0, ak. Так, на рис. 246 вместо
A0A1A2A3A4A5A6A7 можно взять простую цепь A0A1A2A6A7 с теми же концами.
Граф называется связным, если любые две его вершины могут быть соединены цепью. Несвязный граф может быть разбит на не- сколько отдельных связных графов, называемых компонентами ис- ходного графа. На рис. 246 изображен граф, состоящий их трех ком- понент.
Пусть A и B — две вершины связного графа G. Наименьшее из таких чисел k, что в G существует цепь из k ребер, соединяющая вершины A и B, называется комбинаторным расстоянием между вер-
шинами A и B в графе G. Наибольшее из комбинаторных расстояний между вершинами графа G называется комбинаторным диаметром графа G. Например, полный граф с n вершинами имеет комбинатор- ный диаметр 1. Граф, изображенный на рис. 247, имеет комбинатор- ный диаметр 2. Граф, представляющий собой простой контур с n вершинами (рис. 248), имеет своим комбинаторным диаметром число
n2 или n −2 1 (в зависимости от четности числа n). Доказать это предо-
ставляется читателю.
Самая первая работа по теории графов появилась в 1736 году. Она принадлежит перу величайшего математика Леонарда Эйлера, о некоторых результатах которого мы уже говорили выше. Эйлер ис-
следовал головоломку о Кенигсбергских мостах. Город Кенигсберг
(ныне Калининград), расположенный на двух берегах реки Прегель и на двух островах, имел в то время семь мостов (рис. 249). Головолом- ка состояла в том, чтобы совершить прогулку по городу, маршрут которой проходил бы ровно один раз по каждому мосту. Сопоставим с планом города некоторый граф: на рис. 250 вершины L и R соот- ветствуют левому и правому берегам, вершины A и B — островам, а каждое ребро — мосту. Заметим, что граф содержит кратные ребра: вершина B соединена с каждой из вершин L, R двумя ребрами. Задача заключается в том, чтобы решить, можно ли нарисовать этот граф
Рис. 245 |
Рис. 246 |
Рис. 247 |

190 |
Беседа 10. Комбинаторные задачи о графах |
«одним росчерком», т. е. найти в нем самопересекающуюся цепь, проходящую (по одному разу) по всем ребрам.
Можно поставить следующую, более общую проблему, которая и была решена Эйлером. Связный граф G, возможно, содержащий крат- ные ребра, называется уникурсальным («одноросчерковым»), если его весь можно пройти непрерывным движением, не проходя одно и то же ребро дважды, т. е. если в нем существует самопересекающаяся цепь, содержащая в определенной последовательности все ребра. Го- ловоломка о кенигсбергских мостах как раз и сводится к вопросу, является ли граф на рис. 250 уникурсальным.
Эйлер предложил следующее решение проблемы уникурсальнос- ти. Предположим, что связный граф G уникурсален, т. е. в нем суще- ствует путь, начинающийся в некоторой вершине A и оканчивающий- ся в некоторой вершине Z (возможно, совпадающей с A), который по одному разу проходит каждое ребро. Пусть C — произвольная вер- шина графа G, отличная от A и Z. Рассмотрим все ребра, имеющие вершину C своим концом. Рассматриваемый путь, обходящий граф G, подходя к вершине C по некоторому ребру, сразу же уходит из
C по другому ребру (рис. 251). Если впоследствии он снова приходит
вC по третьему ребру, то тут же уходит из C по четвертому (рис. 252) и т. д. Из этого видно, что в вершине C сходится четное число ребер, т. е. индекс вершины C четен. Итак, индексы всех вершин графа G, кроме может быть, A и Z, четны. Из аналогичных соображений вытекает, что вершины A и Z, если они не совпадают, имеют нечет- ные индексы. Если же A и Z совпадают (т. е. мы заканчиваем путь в той же вершине, из которой исходили), то и эта вершина имеет четный индекс.
Итак, если связный граф уникурсален, то все его вершины, кроме, может быть, двух, имеют четные индексы. Это и есть эйлерово усло- вие уникурсальности. Оно, как показывают проведенные выше рас- суждения, является необходимым, т. е. связный граф, который ему не удовлетворяет, уникурсальпым быть не может. На рис. 253 приведены примеры графов, не являющихся уникурсальными.
Однако эйлерово условие не только необходимо, но и достаточно,
т. е. связный конечный граф G в том и только в том случае уникурсален, если он содержит не более двух вершин с нечетными индексами. Заме-
тим, что только одну вершину с нечетным индексом граф иметь не
Рис. 248 |
Рис. 249 |
Рис. 250 |

44. Цепи и циклы в графах |
191 |
может (в силу заключительного утверждения, содержащегося в пре- дыдущем пункте).
Доказательство того, что эйлерово условие является не только необходимым, но и достаточным условием уникурсальности, чуть сложнее, но проводится аналогичным образом. В самом деле, пусть G — граф, все вершины которого имеют четные индексы, и A — произвольная его вершина. Будем, начиная от A, проводить цепь «как попало», пока это возможно. Сколько бы раз мы ни проходили вершину C, отличную от A, всегда останется хотя бы одно ребро, по которому можно уйти из вершины C (поскольку C имеет четный индекс). Поэтому вычерчиваемая цепь не может окончиться нигде, кроме A (а окончиться она должна, поскольку ребер конечное число). Если полученная замкнутая цепь K проходит по всем ребрам, наша цель достигнута.
Если же это не так, то найдется такая вершина Q цепи K, к которой примыкает ребро p′, не вошедшее в цепь K (рис. 254). В этом случае мы, идя вдоль цепи K от вершины A и достигнув вершины Q, не пойдем дальше вдоль цепи K, а сначала совершим вспомога- тельную прогулку, т. е. пойдем по ребру p′ и будем идти «как попало» по ребрам, не вошедшим в цепь K. При этом мы обязательно вернемся к вершине Q (больше нигде эта вспомогательная прогулка окончиться не может в силу соображений четности). Вернувшись в вершину Q, мы затем пойдем дальше вдоль цепи K. В результате получится вместо K другая цепь, проходящая по большему числу ребер. Если эта новая цепь содержит все ребра, то цель достигнута. Если же нет, — мы снова применим тот же прием к цепи и т. д. В конце концов (в силу конечности числа ребер) мы получим цепь, обходящую все ребра графа G. Этим достаточность доказана для графа, все вершины ко- торого имеют четные индексы.
Наконец, если граф G содержит две вершины A и Z с нечетными индексами, мы можем применить то же рассуждение, начав путь из вершины A и закончив его в Z.
Доказанная теорема позволяет, в частности, получить правило обхода лабиринта. Рассмотрим некоторый лабиринт (рис. 255). Пусть нам поставлена задача дойти до сокровища, запрятанного в глубине этого лабиринта, и вернуться обратно. Поскольку мы не знаем, где именно запрятано сокровище, мы должны обойти весь лабиринт,
Рис. 251 |
Рис. 252 |
Рис. 253 |

192 |
Беседа 10. Комбинаторные задачи о графах |
|
|
Рис. 254 |
Рис. 255 |
Рис. 256 |
включая возможные тупики. Проведем средние линии всех коридоров лабиринта — это будут ребра графа G, а вершинами станут пере- крестки и тупики лабиринта (рис. 256). Теперь заменим каждое ребро графа G двукратным ребром (рис. 257). Получившийся граф обозна- чим через G*. В графе G* каждая вершина имеет четный индекс и потому он уникурсален (по теореме Эйлера), т. е. можно найти цепь, обходящую все его ребра. Если такую цепь нам удастся найти, то это означает, что мы пройдем дважды каждое ребро графа G, т. е. обой- дем весь лабиринт, проходя каждый коридор два раза (например, туда и обратно).
Итак, начнем путешествие по лабиринту, отправляясь от вершины A графа G* (от входа в лабиринт; рис. 258). Чтобы не проходить никакой коридор более двух раз, условимся после прохождения каж- дого перекрестка ставить стрелку (по направлению движения) на стене того коридора, по которому мы ушли от этого перекрестка. Тогда второй раз мы в том же направлении по этому коридору не пойдем (а если когда-нибудь снова попадем на этот перекресток, то уйдем по другому коридору, еще не помеченному стрелкой). Это обеспечит нам возможность заведомо выйти из лабиринта (ибо цепь может окончиться только в начальной вершине A).
Однако это еще не все: хотя мы непременно выберемся из лаби- ринта, а не будем блуждать в нем вечно, но, возможно, мы обойдем не весь лабиринт и не доберемся до сокровища (рис. 258). Чтобы избежать этого, условимся, что когда мы в первый раз будем попадать на какой-то перекресток, мы будем ставить кружок на стене того
Рис. 257 |
Рис. 258 |
Рис. 259 |
44. Цепи и циклы в графах |
193 |
|
|
Рис. 260 |
Рис. 261 |
коридора, по которому мы на этот перекресток пришли. Теперь правило обхода лабиринта гласит: от каждого перекрестка разреша- ется уходить по коридору, помеченному кружком, только после того, как все остальные коридоры, отходящие от этого перекрестка, уже были пройдены. Читатель докажет самостоятельно, что при соблю- дении этого правила мы обойдем весь лабиринт и непременно завла- деем сокровищем.
В заключение сформулируем проблему, в некотором смысле про- тивоположную проблеме уникурсальности. Вопрос заключается в том, чтобы решить, существует ли в данном связном конечном графе G такой простой цикл, который проходит через все его вершины. Иными словами, существует ли в графе G «прогулка», позволяющая посетить все его вершины, причем каждую вершину только один раз. В отличие от задачи уникурсальности здесь надо пройтись не по всем ребрам, а через все вершины.
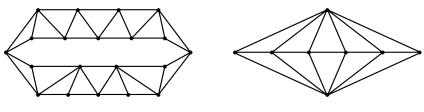
Проблема эта была на частном примере предложена известным ирландским математиком сэром Уильямом Гамильтоном в 1859 году. Гамильтон предложил обойти все вершины правильного додекаэдра (рис. 259), двигаясь по его ребрам и проходя каждую вершину лишь один раз. Головоломка эта имеет положительное решение (т. е. тре- буемый цикл на додекаэдре существует). Вскоре головоломку забыли, но проблему, сформулированную выше, назвали именем ее изобрета- теля: граф, в котором существует простой цикл, обходящий все вер- шины, называется гамильтоновым графом. В отличие от проблемы уникурсальности, эта проблема в общем случае не решена, т. е. неиз- вестно условие (необходимое и достаточное), при выполнении кото- рого граф является гамильтоновым. Примеры гамильтоновых графов приведены на рис. 260, 261.
Задача эта имеет интересное обобщение: на ребрах гамильтонова графа указаны некоторые числа, означающие «стоимости проезда» по этим ребрам, и требуется найти «наиболее дешевый» гамильтонов цикл (т. е. обойти все вершины по разу с наименьшими затратами). Проблема эта, известная под названием «задачи о странствующем торговце», не решена в общем случае, т. е. метод нахождения требу- емого пути в общем случае неизвестен.
