Здесь n = 60 (исследуются 60 минут часа пик, т. е. последователь- ные испытания состоят в том, что берется первая минута, затем вторая, третья, ..., 60-я). В этой ситуации λ = np = 60 0,0122 = 0,732, т. е.

λ невелико по сравнению с n. По формуле (16) находим:

P0 ≈ e−λ ≈ 0,481, P1 ≈ 11! λe−λ ≈ 0,352,

Аналогичным образом по формуле Пуассона рассчитываются ча- стоты телефонных вызовов (если λ невелико, т. е. линия не очень загружена): вероятность P0 того, что в данную минуту часа нет ни

одного вызова, вероятность P1 поступления ровно одного вызова в данную минуту, вероятность P2 двух одновременных вызовов (и тогда

если линия занята первым вызывающим, то второй слышит частые гудки, а в современных телефонах можно поговорить втроем) и т. д.

В частности, 1 − P0 есть вероятность того, что в течение этой минуты будет хотя бы один вызов.

Задачи и упражнения

136. Вероятность попадания торпеды в цель равна 1/3. Сколько следует выпустить торпед, чтобы вероятность попадания в цель хотя бы одной была больше, чем 0,9?

137. На экзамене студенту задается 10 вопросов, на которые он должен ответить «да» или «нет». Какова вероятность, что он ответит правильно не меньше, чем на 7 вопросов, если он отвечает наугад?

138. Рейс из A в B совершают два самолета: двухмоторный и четы- рехмоторный. Вероятность выхода из строя каждого из моторов равна p. Двухмоторный самолет может продолжать полет и на одном моторе, а четырехмоторный — на трех и на двух моторах, а на одном уже не может. При каких значениях p безопаснее лететь на двухмоторном самолете?

139. В булочке с изюмом в среднем бывает 3 изюминки. Какова веро- ятность, что в купленной булочке не окажется изюминок?

140. Некоторую редкую группу крови имеет в среднем один человек на тысячу. У скольких людей нужно взять кровь на исследование, чтобы с вероятностью, большей 0,5, обнаружить человека с кровью этой группы?

Беседа 8. Случайные величины

36. Математическое ожидание и дисперсия

Сумма очков, выпавших на паре брошенных костей (скажем, синей и красной), может принимать значения 2, 3, ..., 12 с вероят- ностями, указанными в следующей таблице:

(2; 3), (3; 2), (4; 1), каждая из которых реализуется с вероятностью 1/36, так что сумма очков 5 выпадает с вероятностью 4/36 = 1/9. Анало- гично вычисляются и другие вероятности. Сумма очков, выпавших на паре брошенных костей, представляет собой случайную величину, которая может принимать значения 2, 3, ..., 12 с указанными в таб- лице вероятностями.

Если случайная величина X может в результате испытания при- нимать числовые значения x1, x2, ..., xn с вероятностями p1, p2, ...,

называется математическим ожиданием этой случайной величины

(от слова Expectation —ожидание).

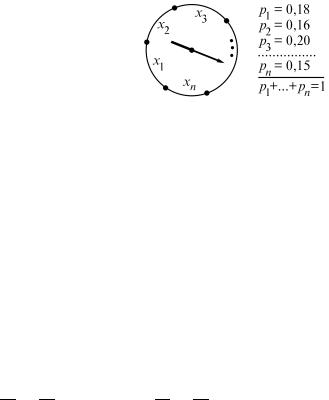
Поясним смысл этого понятия на следующем примере. Колесо рулетки имеет по окружности длину 1. Эта окружность разделена на n дуг, имеющих длины p1, p2, ...,

pn (так что p1 + p2 + ... + pn = 1), и на этих дугах написаны некоторые положительные числа x1, x2, ...,

xn (рис. 207). Если игрок запускает

рулетку (производит испытание), то вращающаяся стрелка укажет после остановки некоторую дугу, и написанное на этой дуге число

будет означать выигрыш игрока. Здесь случайная величина X (выи- грыш) может принимать значения x1, x2, ..., xn с вероятностями p1,

p2, ..., pn. Число (1) означает ожидаемый выигрыш (или «средний»

выигрыш).

Пусть теперь испытание S состоит в пятикратном бросании мо- неты, и число выпадений орла считается «выигрышем». Таким обра- зом, рассматривается случайная величина S5 (выигрыш), которая

может принимать значения k = 0, 1, 2, 3, 4, 5 с вероятностями, которые несложно вычисляются по формуле (15), приведенной в предыдущей беседе:

Математическое ожидание числа выпадений орла, согласно (1),

равно E(S5) = 0321 + 1 325 + 21320 + 31320 + 4325 + 5321 = 8032 = 52.

(при n → ∞) случайная величина Sn превращается в пуассоновскую

величину Y, и мы получаем E(Y) = λ.

В качестве иллюстрации вернемся к игре Шевалье Де Мере. Он 24 раза бросал пару костей и считал успехом выпадение двух единиц.

Здесь вероятность успеха p = 361 . При n = 24 мы имеем pn = 361 24 = 23,

т. е. число λ = pn, в самом деле, невелико по сравнению с n. Поэтому можно применять приближенную формулу (16) из предыдущей бесе- ды. В частности, при k = 0 получается вероятность

2

т. е. вероятность невыигрыша для Де Мере примерно равна 1e 3, как

мы и видели раньше (см. соотношение (2) в предыдущей беседе). Далее, математическое ожидание количества выигрышей

E(Sn) ≈ E(Y) = λ = 23.

Проигрыши де Мере объяснялись не «ошибочностью» математики, а тем, что он не учитывал приближенность замены бернуллиевой слу- чайной величины Sn предельной (пуассоновской) случайной величи-

ной Y.

Второй важной характеристикой случайной величины является ее дисперсия, показывающая разброс возможных значений вокруг мате- матического ожидания (т. е. «среднего» значения). Пусть случайная

величина X имеет математическое ожидание E(X) = µ (см. (1)). Тогда

случайная величина X − µ представляет собой отклонение величины

X от ее среднего значения . Это отклонение может быть положитель- ным, отрицательным или нулем. Квадрат же этого отклонения есть неотрицательная случайная величина; ее математическое ожидание

обозначается через D(X) и называется дисперсией случайной величи- ны X:

Раскрывая скобки и учитывая равенство p1 + p2 + ... + pn = 1 и формулу (1), находим формулу для вычисления дисперсии:

В качестве примера снова рассмотрим пятикратное бросание мо- неты. Здесь, как мы видели, E(S5) = µ = 52. Далее, квадрат (S5)2 случай-

160 Беседа 8. Случайные величины

бросании. Это справедливо и для любой серии испытаний Бернулли: случайная величина Sn, означающая число успехов при n испытаниях,

в каждом из которых вероятность успеха равна р, имеет, как мы видели, математическое ожидание np; дисперсия же ее равна npq:

Читатель может убедиться в этом, проводя тождественные преобра- зования с помощью формулы бинома Ньютона. Однако удобнее при- менить другой прием. Продифференцировав формулу бинома Нью-

n

тона ∑ kn xk = (1 + x)n (сумма по k = 0, 1, ..., n), а затем умножив ре-

k = 0

n

зультат на x, находим ∑ k kn xk = nx(1 + x)n−1. Снова применяя ту же

k = 0

операцию (дифференцирование с последующим умножением на x),

Рис. 208

Первое из этих соотношении означает, что µ = E(Sn) = np (см. (1)), а второе означает, что E((Sn)2) = npq + µ2, т. е. D(Sn) = npq (согласно

(4)). Читатель, возможно, обратил внимание на то, что мы здесь использовали производящую функцию и ее дифференцирование.

Укажем, наконец, что для пуассоновской случайной величины Y (см. (2)) дисперсия, как и математическое ожидание, оказывается

В этом можно убедиться с помощью ряда для ex, причем и в этом случае удобно дважды применить ранее рассматривавшуюся опера- цию (дифференцирование с последующим умножением на x).

Смысл понятия дисперсии можно еще пояснить с помощью меха- нической аналогии. Предположим, что единичная масса разделена на частичные массы m1, m2, ..., mn, которые расположены на числовой

оси в точках с координатами x1, x2, ..., xn (рис. 208). Тогда коорди- ната центра тяжести этой системы масс равна

m1x1 + m2x2 + ... + mnxn = m1x1 + m2x2 + ... + mnxn = µ.

Иначе говоря, если рассматривать x1, x2, ..., xn как значения слу- чайной величины X, а m1, m2, ..., mn — как вероятности этих значе-

ний, то координата µ центра тяжести есть математическое ожидание рассматриваемой случайной величины: E(X) = µ. Далее, согласно (3),

D(X) = m1(x1 − µ)2 + m2(x2 − µ)2 + ... + mn(xn − µ)2,

т. е. дисперсия D(X) представляет собой момент инерции рассматри- ваемой системы масс относительно ее центра тяжести (который с ме- ханической точки зрения как раз характеризует разброс масс относи- тельно центра тяжести системы).

Задачи и упражнения

141. Чему равняется математическое ожидание и дисперсия числа очков, выпадающих при бросании игрального кубика?

142. Ответьте на те же вопросы, если кубик имеет смещенный центр тяжести и вероятность выпадения каждой грани пропорциональна числу, указанному на этой грани.

143. Известна следующая игра. Игрок называет число от 1 до 6. Второй бросает три игральных кости (или три раза подряд одну кость). Если