Глава II. КОМБИНАТОРИКА

Беседа 6. Размещения, сочетания и родственные задачи

23. Размещения с повторениями

Комбинаторику можно назвать количественной теорией конечных множеств. Допустим, мы имеем некоторое конечное универсальное множество U и рассматриваем его подмножества некоторого специ- ального вида (скажем, содержащие данное число элементов). Сколько таких подмножеств имеется в U? Или рассматриваются отображения

U → A некоторого специального вида (где A — заданное конечное множество). Сколько таких отображений существует? Решение этих

ианалогичных задач и составляет содержание комбинаторики.

Вэтом пункте мы рассмотрим вторую из этих задач. Пусть мно-

жество U содержит k элементов, скажем U = {1, 2, ..., k}, а множество

A содержит n элементов. Чтобы задать отображение f: U → A, мы должны указать образы всех элементов 1, 2, ..., k, т. е. указать неко-

торые элементы a1 = f(1), a2 = f(2), ..., ak = f(k) множества A. Иначе говоря, мы должны задать некоторую последовательность a1, a2, ...,

ak, состоящую из k элементов множества A, т. е. задать некоторое

«слово», «буквами» которого являются элементы множества A, при- чем рассматриваются только слова, состоящие из k букв.

Пусть, например, k = 2, причем «алфавит» A состоит всего из трех букв: A = {a, b, c}. В этом случае имеется девять слов:

aa, ab, ac; ba, bb, bc; ca, cb, cc.

В самом деле, на первое место мы можем поставить любую из трех букв a, b, c, и, независимо от этого, мы можем на второе место

поставить любую из трех букв, откуда и получается 3 3 = 9 двухбук- венных слов. А если алфавит A содержит n «букв», то имеется

n n = n2 двухбуквенных слов. Это можно пояснить и так: каждое двух- буквенное слово представляет собой пару (a1; a2) из двух элементов

a1 A, a2 A, т. е. такое слово есть элемент произведения A×A, а это

произведение содержит n2 элементов.

Далее, из алфавита A, содержащего n букв, можно составить n3

трехбуквенных слов. В самом деле, мы имеем n2 двухбуквенных слов, и к каждому из них можно приписать на третьем месте любую из n

букв, т. е. получается n2 n = n3 трехбуквенных слов. Теперь уже понят- но, что k-буквенных слов, при составлении которых используется n

букв, всего имеется nk (на самом деле это «понятно» означает, что можно провести математическую индукцию по k). Например, из рус- ского алфавита, содержащего 32 буквы (включая ё, й, ь, ъ), можно

составить 324 = 1048576 четырехбуквенных слов (если, конечно, не

обращать внимания на семантическую значимость, т. е. допускать любые слова, скажем, «иуэо» или «ьььь»).

Рассмотренную задачу можно охарактеризовать как задачу о раз- мещении n букв на k последовательных местах, причем в одном слове могут повторяться одинаковые буквы. Поэтому говорят о размеще-

ниях с повторениями.

Возвращаясь к отображениям, мы можем сформулировать полу- ченный результат следующим образом: существует nk отображений множества U = {1, 2, ..., k} в множество A, содержащее n элементов.

Можно рассмотреть более общий случай, когда используются «буквы» из двух (или нескольких) «алфавитов». Пусть, например,

рассматриваются слова из p + q букв, в которых первые p букв при- надлежат алфавиту A, содержащему m букв, а последующие q букв принадлежат алфавиту B, содержащему n букв.

Тогда первые p букв дают слово из алфавита A (таких слов имеется m p), а последующие q букв составляют слово из алфавита

B (таких слов имеется nq). Так как любому способу записать первые p букв можно сопоставить любой из способов записи последующих

q букв, то всего имеется m pnq требуемых слов.

Пусть, например, номер автомашины содержит четыре цифры и три буквы (скажем, 6257 МТА), причем используются десять цифр 0, 1, 2, ..., 9 и 27 букв русского алфавита (поскольку ё, й, ь, ъ, ы исключаются). Тогда на первых четырех местах мы можем написать

104 комбинаций цифр, из которых, однако, надо исключить неисполь- зуемую комбинацию 0000, т. е. имеется 9999 допустимых комбинаций

цифр. Буквенных же комбинаций имеется 273. Таким образом, можно написать 9999 273 = 196 810 317 всех мыслимых автомобильных номе- ров рассматриваемого вида.

Отдельного рассмотрения заслуживает случай, когда «алфавит» A состоит только из двух букв A = {0, 1}. Сколько в этом случае существует отображений U → A? Ответ не кажется интересным: по- скольку n = 2, то из рассмотренного ранее общего результата вытека-

ет, что имеется 2k отображений f: U → {0, 1}, если, как и прежде, U содержит k элементов. Однако этот подсчет допускает интересную трактовку.

Каждое отображение f: U → {0, 1} однозначно определяется, если

u (cM). Иначе говоря, каждое отображение f: U → {0, 1} представ-

ляет собой характеристическое отображение некоторого подмноже-

ства M U. Сколько подмножеств, столько и отображений, а отобра- жений, как мы знаем, имеется 2k. Следовательно, множество U,

106 Беседа 6. Размещения, сочетания и родственные задачи

содержащее k элементов, имеет 2k подмножеств (включая пустое множество и само множество U).

В связи с этим множество всех подмножеств множества U принято

обозначать через 2U (оно содержит 2|U| элементов). Это обозначение применяется и в том случае, когда множество U бесконечно.

В этой связи отметим (хотя это и не относится к комбинаторике конечных множеств) следующую теорему Кантора: для всякого множе-

ства U множество всех его подмножеств имеет бо′льшую мощность,

чем само множество U, т. е. |2U| > |U| (см. упр. 20). В частности, если мы рассмотрим всевозможные подмножества множества R действи- тельных чисел, то они образуют множество, мощность которого боль-

Заметим еще, что 2 0 = 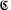— это также было установлено Канто-

ром. Иначе говоря, в множестве натуральных чисел имеется столько же всевозможных подмножеств, сколько имеется действительных чисел. Рассмотрим идею доказательства. Для всякого подмножества

M N можно рассмотреть соответствующее «размещение с повторе- ниями», т. е. последовательность из нулей и единиц, в которой еди- ницы стоят на тех местах, номера которых принадлежат множеству M, а нули — на остальных местах. Например, множеству M, со- стоящему из всех четных чисел, соответствует последовательность 01010101... . Теперь условимся каждую такую последовательность считать бесконечной двоичной дробью, у которой целая часть равна нулю. В частности, множеству всех четных чисел соответствует дво- ичная дробь 0,01010101... (можно доказать, что она изображает

число 13). Таким образом, каждой последовательности из нулей и

единиц (т. е. каждому подмножеству множества N) соответствует не- которое действительное число, принадлежащее отрезку [0; 1]. Этим

определяется некоторое отображение ϕ множества всех подмножеств

множества N в отрезок, т. е. ϕ: 2N → [0; 1]. Если бы это отображение было взаимно однозначным, то мы и получили бы доказательство

равенства 2 0 = 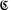. В действительности отображение ϕ является наложением, но взаимно однозначным оно не является; например, бесконечные двоичные дроби 0,10000... и 0,01111... изображают одно

и то же число 12. Эту некорректность можно исправить, т. е. превра-

тить идею в строгое доказательство, но как это сделать, мы здесь говорить не будем.

Задачи и упражнения

76. Сколько существует семизначных чисел, не содержащих цифру 7? 77. Шифр устроен следующим образом: каждой цифре соответствует

одна из трех букв (см. таблицу), а знаку * — одна из двух букв или пробел.

Рассмотрим запись 5545643*8265. Сколькими способами можно ее вос- становить? Какой из них содержателен?

78. Попробуйте найти хотя бы одну осмысленную расшифровку следую-

щей записи: 5343934*150413*6*8156215044414*305041080.

79. Автомобильные номера содержат три буквы и пять цифр, например, Р 502 ВВ 77. Сколько может быть различных автомобильных номеров такого вида?

80. Известна легенда об изобретателе шахмат, который попросил у индийского раджи в награду следующее количество зерен пшеницы: одно на первую клетку, два на вторую, четыре на третью и т. д., удваивая каждый раз количество зерен. В результате получилось количество зерна, которое на земле можно получить лишь за несколько столетий.

Рассмотрим следующую задачу. На каждую клетку шахматной доски либо кладется одно зерно, либо не кладется зерна. Что больше: количество вариантов раскладки или количество зерен, потребованных изобретателем шахмат?

24. Системы счисления

Упомянутая выше двоичная система обозначения чисел (как и другие системы счисления) имеет непосредственное отношение к раз- мещениям с повторениями.

Когда мы говорим «пять тысяч семьсот шестьдесят три», мы имеем в виду число 5 1000 + 7 100 + 6 10 + 3 = 5 103 + 7 102 + 6 10 + 3,

т. е. число, разложенное по степеням десятки с коэффициентами (цифрами), не превосходящими 9. Использование числа 10 в качестве основания системы счисления имеет историческое происхождение, несомненно связанное (полностью или частично) с наличием десяти пальцев на двух руках человека. Имеются и другие системы счисле- ния. Сравнение денежных единиц мина и шеккель, бывших в ходу у древних шумеров и аккадян, привели к созданию шестидесятеричной системы счисления, остатки которой мы встречаем и сегодня (минута

содержит 60 секунд, а час содержит 60 минут, т. е. 602 секунд; анало- гично при измерении углов: градус, минута, секунда). Для представ- ления цифровой информации на различных носителях (числовая ин- формация на дисках компьютеров, звуковая информация на компакт-дисках и т. п.) широко используются двоичная, восьмеричная

ишестнадцатиричная системы счисления.

Вобщем случае при использовании системы счисления, основа-

нием которой служит натуральное число n > 1, числа записываются в форме

где a1, a2, ..., ak — цифры числа c, каждая из которых может при- нимать значения 0, 1, ..., n − 1 (причем обычно первая слева цифра

108 Беседа 6. Размещения, сочетания и родственные задачи

берется отличной от нуля, поскольку при a1 = 0 можно в записи (1)

просто отбросить первое слагаемое и считать, что число c имеет мень- шее количество цифр). Любое натуральное число однозначно записы-

где черта сверху и верхний индекс n означают, что рассматривается не произведение a1a2 ... ak, а запись числа в системе с основанием n.

При такой записи мы будем допускать, что и первые цифры могут быть нулями: например, «четырехзначными» в десятичной системе бу- дут при таком соглашении числа 0001, 0019, 0162, 5837 и т. п., т. е. все числа, являющиеся при обычном понимании (т. е. без нулей слева) не 6oлее чем четырехзначными.

Количество k-значных чисел (2), т. е. количество слов из k букв в алфавите A = {0, 1, ..., n − 1}, как мы видели выше, равно nk; но так как запись 00 ... 0(n) изображает нуль, а не натуральное число, то

получается nk − 1 записей натуральных чисел в виде (2) (или, более подробно, в виде (1)). И как раз следующее натуральное число, т. е.

nk, представляет собой первое (k + 1)-значное число и записывается в

виде 1 nk + 0nk−1 + ... + 0n + 0. Это рассуждение можно превратить с помощью индукции в корректное доказательство того, что любое натуральное число может быть записано (и притом однозначно) в системе счисления с основанием n.

В такой системе счисления действия выполняются по той же схеме, что и в привычной нам десятичной системе; надо только иметь под руками таблицу сложения и таблицу умножения цифр в этой системе. Например, в восьмеричной системе имеются 8 цифр, а табли- цы сложения и умножения выглядят следующим образом:

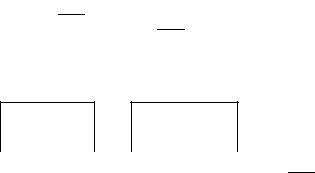
Имея таблицы сложения и умножения, нетрудно производить обычные действия столбиком, повторяя про себя, скажем, «три пи- шем, пять в уме», и т. д. Например, в восьмеричной системе (мы не пишем для простоты записи верхний индекс (8)):