18. Композиция отображений |
73 |
|
|
Рис. 124 Рис. 125 Рис. 126
Если задано произвольное число b [0; ∞), то a = f −1(b), есть прообраз
точки b, т, е. |
такое число |
a [0; ∞), что f(a) = b. Иными словами, |
|
a есть такое |
число, что |
b = √a (см. (4)), |
и потому a = b2, т. е. |
f −1(b) = b2. Это верно для любого b [0; ∞), |
т. е. обратная функция |
||
f −1 определена лишь на луче [0; ∞), а ее значения даются формулой
f −1(x) = x2. Заметим, что функция y = x2 определена для всех действи- тельных x (рис. 125), а не только на луче [0; ∞). Рассматривая ее только на луче [0; ∞), мы и получаем искомую обратную функцию
f −1(x). Ее график (рис. 126) симметричен графику функции (4) отно- сительно биссектрисы первого и третьего координатных углов.
Ограничимся пока этими примерами. Bажные примеры обратных функций мы будем иметь в последующих беседах при рассмотрении тригонометрических и показательных функций. Существенную роль играют обратные отображения и в геометрии, о чем также будет идти речь впоследствии.
Задачи и упражнения
51. Рассмотрим отображение множества действительных чисел в себя, определенное следующим образом: f(x) = x1, если x ≠ 0, и f(0) = 0.
Существует ли у этого отображения обратное?
52. Укажите отрезки действительной прямой, на которых функция f(x) = x3 − x2 имеет обратную.
53. Рассмотрим функцию f(x) = x + [x] (функция [x] определена в упраж- нении 50), отображающую множество действительных чисел в себя. Имеет ли эта функция обратную? Имеет ли она обратную на интервале (100; 101)?
54. Существует ли отрезок, на котором функция Дирихле имеет обрат- ную?
55. Пусть функции f(x) и g(x) отображают множество действительных
чисел на себя и имеют обратные. Bерно ли, что и их сумма также имеет обратную?
18. Композиция отображений
Рассмотрим три множества A, B, C, и пусть даны некоторые отображения f: A → B, g: B → C. Их можно записать в виде «цепоч- ки»:
74 |
Беседа 4. Отображения |
|
|
|
|
|
f g |
(5) |
|
A → B → C. |
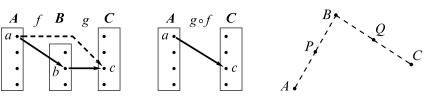
Для каждого элемента a A определен его образ b = f(a), содер- жащийся в множестве B. В свою очередь для этого элемента b B
определен его образ c = g(b), содержащийся в множестве C (рис. 127). Поставим в соответствие элементу a сразу этот элемент с, минуя промежуточное множество B (пунктирная линия на рис. 127). Мы получаем таким образом некоторое отображение множества A в мно- жество C (рис. 128). Оно называется композицией отображений f и g и обозначается через g f.
Обратите внимание: первое применяемое отображение (т. е. f ) пишется справа, а отображение g, применяемое вторым, — слева. Такая форма записи применяется по следующим соображениям. Эле- мент c, который в результате композиции ставится в соответствие
элементу a, имеет вид c = g(b), где b = f(a) — образ элемента a при первом отображении. Таким образом, c = g(b) = g(f(a)). B этой записи
g(f(a)) отображение g оказывается записанным слева, и именно в таком порядке записываются f и g при обозначении композиции: f справа, g слева. Итак, по определению
(g f )(a) = g(f(a))
для любого a A.
Например, если f — центральная симметрия плоскости β относи- тельно точки P, а g — центральная симметрия относительно точ- ки Q (рис. 129), то композиция g f отображений f: β → β и g: β → β представляет→собой параллельный перенос на вектор, вдвое больший,
чем вектор PQ. Иначе говоря, для любой точки A β ее образ C при
→ →
отображении g f определяется равенством AC = 2 PQ (рис. 130).
Еще один пример получается, если взять в качестве f осевую симметрию относительно прямой k, а в качестве g — осевую симмет- рию относительно прямой l, причем k и l пересекаются в некоторой точке O. Из рассмотрения рис. 131, на котором отмечены равные углы, нетрудно заключить, что точка A переводится композицией
g f в такую точку C, что угол AOC вдвое больше угла α между прямыми k и l, причем точки A и C находятся на одинаковом рас-
Рис. 127 |
Рис. 128 |
Рис. 129 |
18. Композиция отображений |
75 |
стоянии от точки O. Иначе говоря, композиция g f представляет собой поворот плоскости β вокруг точки O на угол 2α (рис. 132).
Приведенные примеры показывают, что операция композиции отображений играет важную роль при рассмотрении геометрических преобразований, а мы еще будем в последующих беседах говорить, следуя Феликсу Клейну, о том, что геометрические преобразования
— это подлинная основа всей элементарной (и не только элементар- ной) геометрии. Композиция отображений играет важную роль и в алгебре, где она связана с понятием сложной функции. Рассмотрим этот вопрос подробнее.
Пусть f(x) и g(x) — две числовые функции. Bначале для простоты рассмотрим случай, когда областью определения каждой из функций f, g является вся числовая прямая, т. е. они представляют собой отображения f: R → R, g: R → R. Тогда можно рассматривать слож-
ную функцию g(f(x)), т. е. композицию g f этих отображений. Иначе говоря, сложная функция получается, если в функцию g(y) подставить
вместо y значение y = f(x).
Рассмотрим, например, биквадратный многочлен
h(x) = x4 − 7x2 + 12. |
(6) |
Здесь удобно рассмотреть вспомогательную функцию y = f(x) = x2. Тогда многочлен (6) принимает вид y2 − 7y + 12, и это дает повод
ввести в рассмотрение еще одну функцию g(x) = x2 − 7x + 12. Компо- зиция g f этих функций, т. е. сложная функция
g(f(x)) = g(y) = y2 − 7y + 12 = x4 − 7x2 + 12
совпадает с многочленом (6). Таким образом, h = g f.
Подобно этому, функция h(x) = sin 5x есть композиция двух функ-
ций f(x) = 5x и g(x) = sin x. В самом деле, полагая y = f(x) = 5x, мы находим: g(f(x)) = g(y) = sin y = sin 5x, т. е. h = g f.
Представление заданной функции в виде композиции более про- стых функций часто используется при решении уравнений. Чтобы рассмотреть этот вопрос, вначале проведем некоторое общее рассуж- дение. Рассмотрим снова «цепочку» отображений (5). Пусть c —
Рис. 130 |
Рис. 131 |
Рис. 132 |
76 |
Беседа 4. Отображения |
|
|
Рис. 133 |
Рис. 134 |
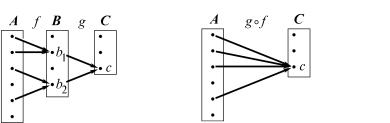
некоторый элемент множества C, и пусть g−1(c) = {b1, b2, ...} B — его прообраз, т. е. b1, b2, ... — все те элементы множества B, которые переводятся отображением g в элемент c (рис. 133). В свою очередь мы можем рассматривать прообразы f −1(b1), f −1(b2), ... этих элемен-
тов при отображении f. Как показывает рис. 134, объединение всех этих прообразов как раз представляет собой прообраз элемента c при отображении g f, т. е.
(g f )−1(c) = f −1(b ) U f −1(b ) U ... . |
(7) |
|
1 |
2 |
|
Пусть теперь задано уравнение |
|
|
g(f(x)) = 0, |
|
(8) |
где g: R → R и f: R → R — некоторые числовые функции. Это урав-
нение имеет вид h(x) = 0, где h = g f — сложная функция, стоящая в левой части уравнения (8).
Решить уравнение h(x) = 0 — значит найти множество всех его корней, т. е. действительных чисел, для которых значение функции h равно нулю. Иначе говоря, решение этого уравнения есть прообраз точки 0, т. е. h−1(0), или, что то же самое, (g f )−1(0). Согласно
сказанному выше, надо сначала найти прообраз g−1(0), т. е. найти все корни b1, b2, ... уравнения g(x) = 0. После этого, согласно формуле (7),
надо найти все прообразы f −1(b1), f −1(b2), ...; их объединение как раз и будет множеством всех корней уравнения (8). Но прообраз f −1(b1) есть множество всех чисел x R, для которых f(x) = b1, т. е. множе-
ство всех корней уравнения f(x) = b1. To же справедливо для f −1(b2) и
т. д.
B результате мы получаем следующее правило: для решения урав-
нения (8) надо сначала найти все корни b1, b2, ... уравнения g(x) = 0,
затем рассмотреть отдельно все уравнения
18. Композиция отображений |
77 |
|
|
f(x) = b1, f(x) = b2, ...; |
(9) |
тогда объединение множеств корней всех получаемых уравнений (9) и представляет собой множество всех корней уравнения (8).
Например, для решения биквадратного уравнения
x4 − 7x2 + 12 = 0, |
(10) |
т. е. уравнения (8), в котором f(x) = x2, g(x) = x2 − 7x + 12, надо сначала решить квадратное уравнение g(x) = 0, т. е. уравнение x2 − 7x + 12 = 0. Оно имеет два корня b1 = 3, b2 = 4. Затем, согласно сформулирован- ному выше правилу, надо рассмотреть отдельно уравнения (9), т. е. в данном случае уравнения x2 = 3, x2 = 4. Множество корней первого из них есть {√3, −√3 }, а множество корней второго есть {2, −2}. Сле-
довательно, их объединение {−2, −√3, √3, 2} и есть множество всех корней биквадратного уравнения (10).
Смысл рассмотренного приема состоит в том, что мы заменяем левую часть уравнения композицией более простых функций, в ре- зультате чего исходное сложное уравнение сводится к решению не- скольких более простых. В школьных задачниках можно найти много уравнений, допускающих применение этого приема.
Существенно заметить, что сложная функция g(f(x)) может рас-
сматриваться и для таких функций f(x), g(x), области определения которых не совпадают со всей числовой прямой. Область определения функции g(f(x)) состоит в этом случае из всех тех x R, для которых, во-первых, x принадлежит области определения функции f, и, во-вто- рых, соответствующее значение f(x) принадлежит области определе- ния функции g. Сформулированное выше правило решения уравнения
(8)остается справедливым и в этом случае. Рассмотрим в качестве примера уравнение
√x − x − 5 −1 = 0. |
(11) |
2 |
|
Его левую часть можно представить в виде √y −1, где y = x2 − x − 5.
Иначе говоря, взяв функции f(x) = x2 − x − 5, g(x) = √x −1, мы как раз запишем уравнение (11) в форме (8). Здесь область определения функ- ции g(x) не совпадает со всей числовой прямой, однако, как мы отмечали выше, это не препятствует применению описанного выше приема. Согласно описанию этого приема мы прежде всего должны рассмотреть уравнение g(x) = 0, т. е. в данном случае √x − 1 = 0. Как легко видеть, это уравнение имеет единственный корень b1 = 1. Сле-
довательно, имеется только одно уравнение (9), а именно уравнение f(x) = b1, т. е.
x2 − x − 5 = 1. |
(12) |
78 Беседа 4. Отображения
Решая его, находим два корня x1 = −2, x2 = 3. Таким образом, множе-
ство всех корней исходного уравнения имеет вид {−2; 3}.
Заметим, что для решения уравнения (11) могут быть применены и другие приемы. Один из них, часто применяемый при решении иррациональных уравнений (т. е. уравнений, содержащих знаки ра- дикалов), состоит в том, что квадратный радикал надо «уединить», а затем возвести обе части уравнения в квадрат. Иначе говоря, надо
переписать уравнение (11) в виде √x2 − x − 5 = 1, а затем от него
перейти «возведением в квадрат» к уравнению x2 − x − 5 = 1.
Как мы видим, получается то же уравнение (12), что и прежде, и это дает те же корни x1 = −2, x2 = 3. Однако возведение обеих частей
уравнения в квадрат может привести к появлению так называемых посторонних корней, в связи с чем такой способ решения требует проверки каждого найденного корня (что, правда, в данном случае несложно). Прием же, рассмотренный ранее (связанный с рассмотре- нием сложной функции), никогда не приводит ни к потере корней, ни к появлению «посторонних» корней, и потому является более пред- почтительным (в тех случаях, когда его удается применить).
Еще один прием решения уравнений заключается в использовании так называемой «области допустимых значений переменной» (сокра-
щенно ОДЗ). Под этим понимается множество всех тех x R, для которых все обозначенные действия выполнимы. В случае уравнения (11) это означает рассмотрение множества всех x R, для которых выражение под знаком квадратного радикала неотрицательно:
x2 − x − 5 ≥ 0.
Сразу же бросается в глаза, что это неравенство существенно сложнее уравнения (12) (например, квадратный трехчлен в левой
части имеет корни 12 (1 ± √21)); к тому же это неравенство вовсе не помогает решению уравнения (11).
Термин ОДЗ, употребляемый только в школе, применяется во многих по- собиях для учащихся и даже в школьных учебниках, но его надо признать неудачным. Ниже, в беседах, посвященных математическим рассуждениям, мы остановимся на этом подробнее, здесь же отметим лишь терминологичес- кие соображения.
Bыполнимость обозначенных действий для данного x R означает, что x принадлежит области определения числовой функции (или пересечению областей определения — например, в случае уравнения типа f(x) = g(x)).
Уже по этой причине использование (только в школе!) термина ОДЗ вместо общепринятого математического термина область определения означает ненужное противопоставление школьного математического преподавания
традициям науки. Кроме того, при рассмотрении функции y = f(x) слово зна- чение употребляется по отношению к y, т. е. это образ точки x при отобра- жении f, это значение откладывается по оси ординат. Применение же термина «допустимое значение» для точки x, принадлежащей области определения (и
18. Композиция отображений |
79 |
потому изображаемой на оси абсцисс), означает лишь создание в психологи- ческом плане условий для путаницы понятий.
Bедь когда мы называем равенство (x + y)2 = x2 + 2xy + y2 тождеством, мы тем самым выражаем наше отношение к этому равенству, имея в виду, что оно справедливо для любых x, y, т. е. речь идет о некоторой теореме.
Когда мы называем равенство f(x) = 0 «уравнением», это также определяет наше отношение к этому равенству, означает постановку вопроса о том, ка- ково множество всех x R, удовлетворяющих этому равенству. И даже если
бы термин ОДЗ выражал что-то математически новое, сам термин «область допустимых значений» этого вопроса не содержит и вряд ли уместен с язы- ковой и психологической точек зрения. А иногда пишут еще «область допус- тимых значений уравнения» ...
B заключение скажем несколько слов о связи обратных отобра- жений с понятием композиции отображений.
Пусть f: A → B — некоторое взаимно однозначное отображение и f −1: B → A — соответствующее обратное отображение. Тогда для лю-
бого a A соотношения f(a) = b и f −1(b) = a равносильны — при ото- бражении f элемент a переводится в b, стало быть, b получается из
a. Следовательно, композиция f−1 f переводит элемент a снова в тот же элемент a, т. е. f −1(f(a)) = f −1(b) = a. Иными словами, f −1 f есть тождественное отображение множества A, т. е. оно переводит каж-
дый элемент a A в себя. Это выражают записью f −1 f = 1A. Анало-
гично отображение f f −1: B → B представляет собой тождественное |
|||
отображение множества B, т. е. f f −1 = 1 . |
|
||
|
|
B |
|
Итак, для взаимно |
однозначного отображения f: A → B и его |
||
обратного отображения f −1: B → A справедливы соотношения |
|
||
f |
−1 f = 1 , |
f f −1 = 1 . |
|
|
A |
B |
|
Bерно и обратное: если отображения f: A → B и g: B → A удовле- |
|||
творяют соотношениям |
|
|
|
|
g f = 1A, |
f g = 1B, |
(13) |
то отображения f, g взаимно однозначны и являются взаимно обрат- ными, т. е. g = f −1.
Заметим, что выполнение только одного из соотношений (13) не достаточно для того, чтобы f и g были взаимно обратными биектив- ными отображениями. Так, отображения, показанные на рис. 135, 136, удовлетворяют первому из соотношений (13), однако взаимно одно- значными не являются (первое из них — вложение, второе — нало- жение).
Рассмотрим в качестве примера функцию f: R → R, заданную фор- мулой f(x) = 2x − 4 (см. (3)), и обратную к ней функцию