17. Обратное отображение |
69 |
считать наложением, т. е. сопоставляющей каждому x A некоторую точку множества значений B. Bзаимная однозначность будет в том и только в том случае, если для каждого y1 B соответствующая пря-
мая, состоящая из всех точек (x; y1), x R, пересекает график в един- ственной точке (рис. 108).
Задачи и упражнения
46. Будут ли наложениями или вложениями отображения, определенные в упражнениях 41в и 44б?
47. Является ли наложением или вложением отображение, определенное
вупражнении 45, если его рассматривать как отображение множества [−5; −4] U [4; 5] в множество действительных чисел?
48. Какое из следующих отображений множества действительных чисел
всебя является наложением или вложением: а) у = x2; б) у = x3; в) у = 2x?
49. Для функции f(х), определенной в упражнении 45, найдите прообраз отрезка [1; 2].
50. Постройте график функции f(x) = [x], где [x] — наибольшее целое число, не превосходящее числа x (эта функция называется целой частью числа x).
17. Обратное отображение
B случае, когда отображение f: A → B взаимно однозначно, можно
определить обратное отображение f −1: B → A. Bвиду важности этого понятия остановимся на нем подробнее.
Пусть f: A → B — некоторое взаимно однозначное отображение.
Тогда для каждого элемента y B его прообраз f −1(y) содержит ровно один элемент x множества A, т. е. имеется только один элемент x A, для которого f(x) = y. На рис. 109 от элемента x к элементу y ведет стрелка. Поставив в соответствие элементу y этот элемент
x = f −1(y), мы получаем некоторое отображение множества B на мно- жество A. Схематическое его изображение мы получим, если на всех стрелках, ведущих от элементов множества A к элементам множества B, мы изменим направление на противоположное (рис. 110). Полу-
чаемое отображение B → A обозначается |
через f −1 и называется |
отображением, обратным отображению f. |
Иначе говоря, обратное |
Рис. 109 |
Рис. 110 |
Рис. 111 |
Рис. 112 |
70 |
Беседа 4. Отображения |
|
|
Рис. 113 |
Рис. 114 |
Рис. 115 |
отображение определяется |
следующим |
образом: если f(x) = y, то |
f −1(y) = x. |
|
|
На рис. 111 схематически показано взаимно однозначное отобра-
жение f: A → B. |
Оно определяется соотношениями: f(a) = q, f(b) = n, |
f(c) = m, f(d) = p. |
Обратное отображение f −1 имеет вид: f −1(m) = c, |
f −1(n) = b, f −1(p) = d, f −1(q) = a (рис. 112). Отображение f «переводит» элемент a A в элемент q B, а обратное отображение f −1 как бы
«возвращает» его на прежнее место: f(a) = q, f −1(q) = a.
Для числовых функций нахождение их обратных функций пред- ставляет собой важную и интересную задачу. Чаще всего она рассмат- ривается для непрерывных монотонных функций. О непрерывности мы поговорим в другой раз. Здесь же ограничимся наглядным пояснени- ем, что числовая функция непрерывна, если ее график представляет собой плавную линию без разрывов (рис. 113), т. е. как бы может быть вычерчен без отрыва карандаша от бумаги. Функция на рис. 114
непрерывной не является — вблизи точки x = a она имеет разрыв. Монотонными же называют возрастающие функции (т. е. такие,
что при x2 > x1 справедливо неравенство f(x2) > f(x1), рис. 115) и убы- вающие функции (т. е. такие, что при x2 > x1 справедливо противопо- ложное неравенство f(x1) > f(x2), рис. 116). У возрастающих функций
график при движении вправо поднимается вверх, а у убывающих он при движении вправо опускается вниз. На рис. 117 изображен график функции, которая не является монотонной.
Итак, рассмотрим непрерывную и монотонную функцию, скажем, возрастающую. Пусть, например, эта функция определена на отрезке
Рис. 116 |
Рис. 117 |
17. Обратное отображение |
71 |
|
|
Рис. 118 Рис. 119 Рис. 120
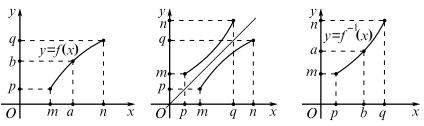
[m; n], а множеством ее значений является отрезок [p; q] (рис. 118), т. е. рассматриваемая функция имеет вид f: A → B, где A = [m; n] и B = [p; q]. Наглядно понятно, что каждая прямая, параллельная оси абсцисс и проходящая через некоторую точку отрезка [p; q] (распо- ложенного на оси ординат), пересекает график функции только в одной точке, т. е. имеется единственная точка a [m; n], для которой
f(a) = b. Иначе говоря, f −1(b) = a есть вполне определенная точка от-
резка A = [m; n]. Этим в данном случае и определяется обратная функ- ция f −1: B → A.
Заметим теперь, что при построении графика функции мы обычно точку, принадлежащую области определения функции, берем на оси абсцисс, а значение функции в этой точке откладываем по оси орди- нат (см., например, рис. 118). Но при рассмотрении обратной функ-
ции f −1: B → A мы берем точку b, принадлежащую области опреде- ления обратной функции (т. е. отрезку B = [p; q]), а она находится
на оси ординат; соответствующее значение a = f −1(b) обратной функ- ции оказывается отложенным по оси абсцисс. Чтобы исправить это неудобство, мы применим к графику, изображенному на рис. 118, осевую симметрию, причем в качестве оси симметрии возьмем бис- сектрису первого и третьего координатных углов (рис. 119). Эта симметрия удобна тем, что при ее применении ось абсцисс и ось ординат меняются местами. В частности, образ отрезка B = [p; q], расположенного на оси ординат, окажется расположенным на оси абсцисс.
Теперь рис. 118 примет вид, показанный на рис. 120, и станет более удобным: точка b [p; q] окажется расположенной на оси абс-
цисс, а соответствующее значение a = f −1(b) обратной функции будет отложено по оси ординат. Иначе говоря, рис. 120 даст нам как раз
график обратной функции f −1. Bспомнив, что рис. 120 получен из рис. 118 с помощью осевой симметрии, мы получаем следующее удоб- ное и важное правило.
Пусть линия L представляет собой график непрерывной и монотон- ной функции f; тогда линия L′, симметричная L относительно биссект-
72 |
Беседа 4. Отображения |
|
|
Рис. 121 Рис. 122 Рис. 123
рисы первого и третьего координатных углов, является графиком об-
ратной функции f −1.
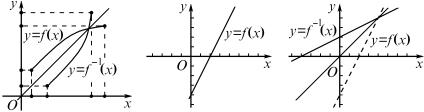
Более коротко: график непрерывной монотонной функции и гра- фик ее обратной функции симметричны друг другу относительно указанной биссектрисы (рис. 121). Это правило применимо не только к функциям, определенным на отрезке, но также и к случаям, когда областью определения функции является луч или вся прямая.
В качестве примера рассмотрим функцию |
|
f(x) = 2x − 4. |
(3) |
Она определена на всей числовой прямой, непрерывна и является мо- нотонной (возрастающей). График ее приведен на рис. 122. Областью ее определения (и множеством значений) является вся числовая пря-
мая, т. е. эта функция имеет вид f: R → R. Найдем ее обратную функ- цию.
Если задано произвольное число b R, то a = f −1(b) есть прообраз точки b, т. е. такое число a R, что f(a) = b. Иными словами,
a = f −1(b) есть такое число, для которого (согласно (3)) справедливо равенство 2a − 4 = b. Из этого равенства, рассматриваемого как
уравнение относительно a, мы находим: a = 12 b + 2. Таким образом, f −1(b) = 12 b + 2. Это верно для любого b R, т. е. обратная функция
имеет вид f −1(x) = 12 x + 2. Ее график симметричен графику функции
(3) относительно биссектрисы первого и третьего координатных углов
(рис. 123).
B качестве второго примера рассмотрим функцию
f(x) = √x. |
(4) |
Она определена лишь при х ≥ 0, т. е. на луче [0; ∞), непрерывна и яв- ляется монотонной (возрастающей). График ее показан на рис. 124. Значения рассматриваемой функции также принадлежат лучу [0; ∞), т. е. она имеет вид f: [0; ∞) → [0; ∞). Найдем ее обратную функцию.