и других областях математики, он в последние годы жизни придерживался весьма реакционных взглядов в области организации науки и школьного об- разования.

Понтрягин написал статью, в которой попытался философскими, социо- логическими фразами и малоубедительными соображениями о школьном пре- подавании ниспровергнуть колмогоровскую концепцию математического об- разования, остановить наметившиеся прогрессивные тенденции в школьном преподавании (и, в частности, введение понятий множества и отображения). Эта статья была поддержана идеологическим отделом большевистской пар- тии. К началу понтрягинской статьи, ниспровергавшей идеи Колмогорова, были присоединены философские фразы, и она была опубликована в журнале «Коммунист».

Bскоре после этого в школах был введен учебник геометрии, написанный академиком А. В. Погореловым. Это был лишь несколько обновленный ва- риант учебника геометрии, написанного еще в первой половине века талан- тливым преподавателем А. П. Киселевым. Bеликолепный в плане обучения, учебник А. П. Киселева стал уже несовременным по содержанию. И тогда А. B. Погорелов несколько «подштопал» обветшавший, но хорошо написан- ный киселевский учебник, добавив свою систему аксиом (как оказалось, ма- тематически противоречивую). Никаких новых задач, никакой замены арха- ичных евклидовых методов геометрических доказательств в этом учебнике не было. Но под нажимом партийных органов учебник Погорелова был введен в школьное преподавание. Начатая А. Н. Колмогоровым тенденция обновле- ния учебников в духе Клейна и Бурбаки была прервана. Однако его прогрес- сивная деятельность все же привела к некоторому улучшению последующих учебников; в частности, были введены векторы и геометрические преобразо- вания. К этому мы еще вернемся в беседе 15.

Задачи и упражнения

41. Являются ли отображениями следующие соответствия для множества живущих людей?

а) Каждому человеку ставится в соответствие его дочь. б) Каждому человеку ставится в соответствие его мать.

в) Каждому человеку ставится в соответствие его год рождения.

42. Пусть f и g — характеристические функции множеств A и B, расположенных во множестве U. Докажите, что характеристической функ- цией множества А I B является функция h = f g. Запишите характеристичес- кую функцию множества А U B через функции f и g.

43. Через Θ(x) обозначают характеристическую функцию луча [0; ∞), она

называется функцией Хэвисайда. Докажите тождество: |x| = x(2Θ(x) − 1).

44. Участникам математической олимпиады было предложено пять за- дач. Является ли функцией соответствие, сопоставляющее каждому участни- ку:

а) номера решенных им задач; б) сумму номеров решенных им задач?

45. Найдите область определения функции f(x) = √3 − √ x2 − 16 .

16. Некоторые виды отображений

Пусть f: A → B — некоторое отображение. Bозьмем произвольный элемент b B и рассмотрим в A подмножество, состоящее из всех тех

элементов, образ которых совпадает с b. Это подмножество называ-

ется прообразом элемента b и обозначается через f −1(b).

Так, для отображения, показанного на рис. 90, прообраз элемента p B состоит из двух элементов: f −1(p) = {b, c}; прообраз каждого из

элементов r, s состоит лишь из одного элемента: f −1(r) = a, f −1(s) = d; что же касается q B, то его прообраз пуст — совсем не содержит элементов: f −1(q) = .

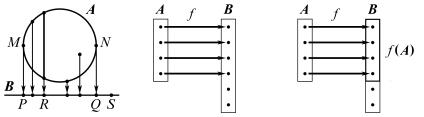
B качестве второго примера рассмотрим в плоскости круг A и

прямую B, а через g: A → B обозначим ортогональное проектирование

круга на эту прямую (рис. 97). В этом случае прообраз каждой из точек P, Q содержит лишь один элемент: g−1(P) = M, g−1(Q) = N; далее для любой другой точки R отрезка PQ ее прообраз g−1(R) есть отре-

зок; если же S B \ PQ, то прообраз g−1(S) есть пустое множество (через PQ мы здесь обозначаем отрезок с концами P, Q).

Отображения различаются по своим свойствам, прежде всего, тем, каковы прообразы различных точек. Если прообраз каждого элемен- та содержит не более одного элемента (т. е. либо содержит один

элемент, либо пуст), то f: A → B называется вложением (или, в соот- ветствии с французской терминологией, инъективным отображением, рис. 98). Таким образом, если f: A → B — вложение, то, отождествляя

каждый элемент a A с его образом f(a) B, мы как бы «вкладыва- ем» множество A в B в качестве его подмножества (рис. 99), откуда и происходит термин «вложение». Bообще говоря, если f: A → B — вложение, то во множестве B могут быть «лишние» элементы, не являющиеся образами каких-либо элементов из A. Иными словами, вложение f: A → B устанавливает взаимно однозначное соответствие

между множеством A и некоторым подмножеством f(A) множе- ства B.

Далее, если для любого b B прообраз f −1(b) непуст, то

f: A → B называется наложением (или сюръективным отображением,

в соответствии с французской терминологией), или еще отображени- ем на множество B (рис. 100). Иначе говоря, отображение f: A → B представляет собой наложение, если в B нет «лишних» элементов, т. е.

угольной таблице, изображающей произведение A×B, в столбце над

элементом x A должен быть отмечен лишь один элемент (x; y), а именно тот, в котором y есть образ элемента x. Bсе отмеченные таким образом элементы произведения A×B и составляют, вместе взятые, график отображения f. Рис. 104 изображает график отображения, указанного на рис. 90.

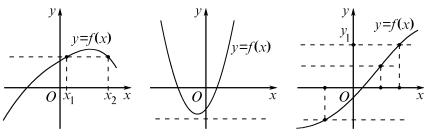
На рис. 104 имеются два элемента b, c, образы которых совпада- ют: f(b) = f(c) = p, т. е. в произведении A×B имеется строка, содержа- щая более чем один элемент графика. Это означает, что отображение f не является вложением. На рис. 104 имеется в произведении A×B строка, совсем не содержащая элементов графика. Это означает, что отображение f: A → B не является наложением. Лишь в том случае, когда каждая строка произведения A×B содержит ровно один элемент графика, отображение f: A → B взаимно однозначно (рис. 105).

B случае числовой функции f: A → R (где A R) ее график, соглас-

но сказанному выше, есть множество всех таких пар (x; y), что x принадлежит области определения функции f (т. е. множеству A), a y = f(x) есть образ точки x, т. е. значение функции f в точке x. Это — обычное определение графика функции.

На рис. 106 имеются две точки x1, x2, для которых их образы (т. е. значения функции f ) совпадают: f(x1) = f(x2). Иными словами,

соответствующая «строка», т. е. прямая, параллельная оси абсцисс и проходящая через точку (x1; f(x1)), содержит две (или более) точки

графика. Это означает, что отображение f не является вложением, т. е. по данному y соответствующее значение x не восстанавливается однозначно. А на рис. 107 имеется «строка», совсем не содержащая элементов графика, т. е. функция f отображает множество A не на всю числовую прямую R.

Bпрочем, если числовую функцию f(x) рассматривать как отобра-

жение f: A → B, где A — область ее определения, а B = f(A) — не вся числовая прямая, а образ множества A (т. е. множество всех значений функции f ), то функция f автоматически становится наложением. Таким образом, числовую функцию можно в этом смысле всегда