
- •Оглавление
- •Предисловие
- •1. Мнения о пользе математики
- •2. Понятия математики и их возникновение
- •3. Некоторые виды абстракции
- •4. Многоступенчатые абстракции
- •6. Количественные отношения реального мира
- •7. Множество и его элементы
- •8. Взаимно однозначное соответствие
- •10. Понятие мощности множества
- •Беседа 3. Операции над множествами
- •11. Пересечение множеств
- •12. Объединение множеств
- •13. Дополнение множеств
- •14. Произведение множеств
- •Беседа 4. Отображения
- •15. Общее понятие отображения и школьная математика
- •16. Некоторые виды отображений
- •17. Обратное отображение
- •18. Композиция отображений
- •19. Классификация
- •Беседа 5. Упорядоченные множества
- •20. Понятие упорядоченного множества
- •21. Минимальные элементы и математическая индукция
- •22. Трансфинитные числа и аксиома выбора
- •Глава 2. Комбинаторика
- •Беседа 6. Размещения, сочетания и родственные задачи
- •23. Размещения с повторениями
- •24. Системы счисления
- •25. Размещения без повторений
- •26. Сочетания без повторений
- •27. Сочетания с повторениями
- •28. Бином Ньютона
- •29. Производящие функции
- •30. Принцип Дирихле
- •Беседа 7. События и вероятности
- •31. События
- •32. Классическое понятие вероятности
- •33. Свойства вероятности
- •34. Условная вероятность
- •35. Независимые события и серии испытаний
- •Беседа 8. Случайные величины
- •37. Нормальное распределение
- •38. Закон больших чисел
- •Беседа 9. Информация
- •40. Количество двоичных цифр
- •41. Задачи на взвешивание
- •42. Понятие об энтропии
- •Беседа 10. Комбинаторные задачи о графах
- •43. Графы и их элементы
- •45. Плоские графы
- •46. Формула Декарта—Эйлера
- •47. Правильные многогранники и паркеты
- •49. Ориентированные графы
- •50. Конечные позиционные игры
- •51. Понятие о сетевом планировании
- •52. Существование и общность
- •53. Структура теоремы
- •54. Отрицание
- •55. Необходимое и достаточное условие
- •56. Конъюнкция и дизъюнкция
- •Беседа 12. Понятие об аксиоматическом методе
- •57. Возникновение аксиоматического метода в математике
- •58. Метрические пространства
- •59. Коммутативные группы
- •Беседа 13. Непротиворечивость, независимость, полнота
- •60. Непротиворечивость и понятие модели
- •61. Математические примеры моделей
- •62. Построение аксиоматики геометрии
- •63. Геометрия Лобачевского
- •64. Модель геометрии Лобачевского
- •65. Изоморфизм моделей
- •66. Полнота аксиоматики
- •67. Цикл озарения
- •68. Сфера достижимости
- •69. Анализ и синтез
- •70. Обратимый анализ
- •72. Поиск решения нестандартных задач
- •Беседа 15. Наглядность. Аналогия. Интуиция
- •74. Формула наглядности — изоморфизм плюс простота
- •75. Наглядность и математическая эстетика
- •76. Аналогия — общность аксиоматики
- •78. Несколько слов о математической интуиции
- •Решения задач и упражнений
- •Предметный указатель

60 |
Беседа 4. Отображения |
Задачи и упражнения
36. Опишите геометрический образ произведения отрезка на окружность. 37. Каков будет геометрический образ произведения двух окружностей? 38. Огромный военный оркестр демонстрировал свое искусство на пло- щади. Сначала музыканты построились в виде квадрата, а затем перестро- ились в прямоугольник, причем число шеренг увеличилось на 5. Сколько
музыкантов в оркестре?
39. Сколько ладей можно поставить на шахматной доске так, чтобы они не били друг друга? Сколько способов такой расстановки?
40. Опишите множество точек координатной плоскости, координаты которых удовлетворяют соотношению |x| + |y| = 1.
Беседа 4. Отображения
15. Общее понятие отображения и школьная математика
Мы говорим, что задано отображение f множества A в множество B, если указано правило, сопоставляющее каждому элементу x A один вполне определенный элемент множества B, называемый образом элемента x и обозначаемый через f(x). Задание отображения f множе-
f
ства A в множество B обозначается записью f: A → B или A → B (a иногда просто A → B, если из текста понятно, о каком отображении
идет речь). Для отображения f: A → B множество A называется его областью определения. На рис. 90 схематически показано некоторое отображение множества A в множество B: от каждого элемента из A проведена стрелка к его образу.
Заметим, что один и тот же элемент множества B может оказаться образом нескольких элементов из A. Так, на рис. 90 элемент p B
является образом каждого из элементов b, c, т. е. f(b) = p и f(c) = p. Может оказаться, далее, что некоторый элемент множества B не является образом никакого элемента из A. Например, на рис. 90 нет в A элемента, образ которого совпадал бы с q. Но для любого
отображения A → B непременно должно быть выполнено условие:
каждому x A сопоставлен только один элемент множества B в качестве его образа. Соответствие, показанное на рис. 91, отображе- нием не является, поскольку элементу c A не поставлен в соответ- ствие никакой элемент множества B (т. е. от c не идет стрелка к какому-либо элементу множества B). Соответствие на рис. 92 также
Рис. 90 |
Рис. 91 |
Рис. 92 |

15. Общее понятие отображения и школьная математика |
61 |
|
|
Рис. 93 |
Рис. 94 |
отображением не является, так как от элемента a A ведут две стрел- ки к элементам множества B, а не одна.
Отображения, рассматриваемые в алгебре и математическом ана- лизе, называют функциями. Чаще всего функции задаются формула- ми. Например, запись
f(x) = x2 − 3x + 5 |
(1) |
означает, что каждому действительному числу x сопоставляется в ка- честве его образа (или, как говорят, значения этой функции в точке x) число, определенное правой частью равенства (1). Например,
f(2) = 3, f(0) = 5, f(−2) = 15. Поскольку в качестве x может быть взято любое действительное число, областью определения этой функции яв- ляется все множество R действительных чисел. И образ f(х) (т. е. зна- чение этой функции в точке x) также является действительным чис- лом, т. е. формула (1) задает функцию (отображение) f: R → R. Функ-
ция g(x) = √x − 5 имеет своей областью определения луч [5; ∞), т. е. множество всех действительных чисел, удовлетворяющих неравенству х ≥ 5 (поскольку при х < 5 выражение под корнем становится отрица- тельным), т. е. эта запись определяет функцию (отображение)
|
|
g: [5; ∞) → R. |
|
|
|
|||
А запись |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
h(x) = |
|
|
|
|
(2) |
|
|
|
(x − 5)√x |
|
|
||||
определяет |
функцию |
(отображение) |
h: A → R, где множество |
A, |
||||
являющееся |
областью |
определения |
этой |
функции, |
имеет |
вид |
||
А = (0; 5) U (5; ∞), т. е. представляет собой |
объединение |
интервала |
||||||
(0; 5), определяемого неравенствами 0 < x < 5, и луча (5; ∞), состояще-
го из всех точек, удовлетворяющих неравенству x > 5. Отметим, что от отрезка [a; b], состоящего из всех чисел, удовлетворяющих нера- венствам a ≤ x ≤ b (рис. 93), интервал (a; b) отличается тем, что он не содержит концевые точки x = a и x = b, т. е. определяется неравен- ствами a < x < b (рис. 94).
Bообще, когда говорят, что рассматривается некоторая числовая функция f(х), то имеют в виду задание некоторого отображения
f: A → R, где A R. Числовые функции могут задаваться не только формулами, но и описательно. Такова, например, функция Дирихле, определяемая следующим образом:

62 Беседа 4. Отображения
0, если число х иррационально, f(x) =
1, если число х рационально.
Например, f(1) = 1, f 72 = 1, f(√2 ) = 0, f(π) = 0. Несмотря на то, что эта
функция не записана формулой, она принимает вполне определенное значение (0 или 1) для любого x R.
B качестве еще одного примера рассмотрим так называемую ха- рактеристическую функцию множества. Пусть A — некоторое под-
множество числовой прямой R. Зададим числовую функцию ϕ(x), определенную на всей числовой прямой R, следующим образом:
1, если х A,
ϕ(x) =
0, если х A.
Это и есть характеристическая функция множества A. Если, напри- мер, A есть множество всех рациональных чисел, то характеристичес- кая функция этого множества совпадает с рассмотренной выше функ-
цией Дирихле.
Отображения рассматриваются и в геометрии. Bсе геометрические преобразования, играющие важную роль в этой области математики, являются отображениями. Например, центральная симметрия с цент- ром O есть отображение, которое каждой точке A, отличной от O, ставит в соответствие такую точку B, что отрезок AB имеет O своей серединой. Точке же O ставится в соответствие сама точка O, т. е. как говорят, точка O является неподвижной точкой этого отображе- ния. На рис. 95 образом точки A при центральной симметрии отно- сительно точки O является точка B, образом точки B является A, образом точки C является D, образом точки D является C, образом точки O является O. Обозначая эту симметрию буквой s, мы можем
написать: s(A) = B, s(B) = A, s(C) = D, s(D) = C, s(O) = O.
π
Поворот r плоскости P на угол 2 вокруг центра O также пред-
ставляет собой некоторое отображение r: P → P этой плоскости на ту же самую плоскость. Точку A, отличную от O, это отображение переводит в такую точку B = r(A), что A и B лежат на одной окруж- ности с центром O и величина угла AOB, отсчитываемая в положи-
тельном направлении (т. е. против хода часовой стрелки), равна π2
(рис. 96). Точка O переводится рассматриваемым поворотом в ту же точку O, т. е. O является неподвижной точкой этого отображения. Bообще, любое геометрическое преобразование f плоскости P (осевая симметрия, параллельный перенос, гомотетия и многие другие)
представляет собой некоторое отображение f: P → P . Иначе говоря, каждое геометрическое преобразование f плоскости P есть как бы «геометрическая функция», которая, однако, в отличие от числовой
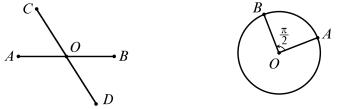
15. Общее понятие отображения и школьная математика |
63 |
|
|
Рис. 95 |
Рис. 96 |
функции, имеет своей областью определения не некоторое множество чисел, а множество P, состоящее из точек, и образами также являются
не числа, а точки, т. е. для любой точки A P ее образ B = f(A) также есть некоторая точка плоскости P.
Таким образом, рассмотрение не только множеств, но и отобра- жений сближает алгебру и геометрию, т. е. составляет некоторый общий взгляд на эти разделы школьной математики.
Попытки модернизировать школьный курс математики, весьма сильно отстававший от современной науки, были сделаны во многих странах мира в середине XX столетия. Чтобы рассказать об этом, мы начнем издалека.
Три русских писателя, братья Жемчужниковы и Алексей Констан- тинович Толстой, выпустили интересную и весьма известную книгу, назвав ее сочинениями Козьмы Пруткова. Этим псевдонимом они охарактеризовали напыщенного и самонадеянного вымышленного автора, который назидательно высказывал вроде бы банальные, но, если вдуматься, очень глубокие истины. А в середине XX столетия группа французских математиков (Картан, Дьедонне и ряд других ученых) создала «математического Козьму Пруткова», издав серию
книг под псевдонимом Никола′ Бурбаки′. Художники создали и пор- трет этого вымышленного самодовольного автора, генерала в отстав- ке, который решил остаток жизни посвятить написанию трактатов о математических науках. Книги Бурбаки по разным разделам матема- тики являются ультрасовременными и содержат много интересных идей, объединяющих общим взглядом различные ветви математики, главным образом на базе теории множеств и топологии. Эти десятки трактатов Бурбаки внесли существенный вклад в формирование ма- тематических взглядов современных ученых, особенно молодых. Лю- бопытен эпизод, связанный с международным математическим кон- грессом, проходившим в 1966 году в Москве. При подготовке этого конгресса оргкомитет разослал во все страны мира извещение о предстоящем математическом форуме. Каждый математик, имевший научные публикации, получил приглашение принять участие в работе конгресса, для чего он должен был написать о своем согласии и выслать оргвзнос в размере 40 американских долларов. Получил такое приглашение и Никола Бурбаки, автор десятков широко извест- ных книг. Эта шутка московского оргкомитета была подхвачена

64 |
Беседа 4. Отображения |
французскими математиками, которые не пожалели 40 долларов и сообщили, что известный французский математик выражает свое со- гласие участвовать в работе конгресса. И перед началом одного из пленарных заседаний конгресса в фойе было вывешено кричащее объявление, извещавшее о том, что в этот день, после заседаний, в пресс-центре конгресса состоится встреча с известным французским математиком Никола Бурбаки...
Модные теоретико-множественные концепции Бурбаки сопрово- ждались и некоторой ревизией математических обозначений. Так,
числовой интервал, издавна записываемый в виде (a; b), Бурбаки предложил обозначать символом ]a; b[, в котором «вывернутые» квад- ратные скобки должны были символизировать то, что, в отличие от отрезка [a; b] интервал ]a; b[ не содержит своих концевых точек, т. е.
описывается неравенствами a < x < b.
Bсеобщее увлечение идеями Бурбаки совпало по времени с про- цессом модернизации школьного образования (а может быть, не толь- ко «совпало» по времени, но и было органически связано с этим процессом). Новые учебники, изданные в ряде стран мира, уделяли существенное внимание рассмотрению множеств и отображений. В алгебре это выражалось, в частности, в том, что рассматривалось множество всех решений уравнения или неравенства, и оно записы-
валось с помощью знаков , , U, I. Мы это видели на примере неравенства (6) и его решения (7) в пункте 12.
Разумеется, дело не в обозначениях, а в самих идеях множества и отображения, в удобстве математического языка, использующего эти понятия и объединяющего алгебру с геометрией. В геометрии идеи этого круга были связаны с прогрессивной тенденцией, восходящей к замечательному немецкому математику и педагогу Феликсу Клейну, который говорил о широком использовании геометрических преоб- разований взамен устаревших евклидовых приемов геометрических доказательств (об этом еще будет идти более подробный разговор в последующих беседах).
В России попытка модернизировать школьный курс математики и свя- занная с нею реформа школьного обучения были особенно драматичны. Ини- циатором и активным руководителем реформы школьного математического образования стал выдающийся математик XX столетия академик Андрей Ни- колаевич Колмогоров. Правда, созданный по новой программе курс геомет- рии оказался трудным. Но в идейном плане это был совершенно новый курс, содержавший современные идеи и способствовавший более глубокому осмыс- лению математики, чем прежние учебники. И хотя новые учебники были трудными для школьного учителя, но в течение 2 – 3 лет работы по этим учебникам школьные преподаватели их освоили, «пропустили через свое
сердце» и стали на три головы выше в своем идейном понимании математики. И тут грянул гром среди ясного неба. Начался «крестовый поход» против колмогоровских идей и против употребления в школе множеств и других новых для школы понятий, возглавленный академиком Л. С. Понтрягиным. Личность Л. С. Понтрягина весьма противоречива в истории науки. Талан- тливый математик, получивший ряд первоклассных результатов в топологии
