
Информатика
.pdf
Т е м а 3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
ЛАБОРАТОРНАЯ РАБОТА № 6
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ПРОСТЫХ ИТЕРАЦИЙ И МЕТОДОМ ЗЕЙДЕЛЯ
Метод простых итераций. Рассмотрим применение метода про-
стых итераций на примере решения системы линейных уравнений размерности 3´3. Согласно данному методу, исходная система преоб- разуется следующим образом:
ìa x + a x + a x = b |
|
ìx1 = (b1 - a12 x2 - a13 x3 ) / a11 |
|||||||||||||||
ï |
11 |
1 |
12 |
2 |
13 |
3 |
1 |
|
ï |
|
= (b2 - a21x1 - a23 x3 )/ a22 Þ |
||||||
ía21x1 + a22 x2 + a23 x3 = b2 |
Þ íx2 |
||||||||||||||||
ï |
|
|
+ a32 x2 + a33 x3 = b3 |
|
ï |
|
= (b3 - a31x1 - a32 x2 )/ a33 |
||||||||||
îa31x1 |
|
îx3 |
|||||||||||||||
|
|
|
|
ìx1 |
= (b - a x0 |
- a x0 )/ a |
|
|
|||||||||
|
|
|
|
ï |
1 |
|
1 |
12 |
|
2 |
13 |
3 |
11 |
|
|||
|
|
|
|
íx12 = (b2 - a21x10 - a23 x30 )/ a22 |
|||||||||||||
|
|
|
|
ï |
|
= (b - a |
|
x0 |
- a |
|
x0 ) / a |
|
, |
||||
|
|
|
|
ïx1 |
31 |
32 |
33 |
||||||||||
|
|
|
|
î |
3 |
|
3 |
|
|
1 |
|
2 |
|
|
|||
где a11 ¹ 0 , a22 ¹ 0 , a33 ¹ 0 .
Полученные формулы позволяют найти первое приближение к реше- нию ( x11, x12 , x31 ). В качестве начального приближения ( x10 , x20 , x30 ), как правило, используются значения ( b1,b2 ,b3 ) или (0,0,0).
Вычисление (k+1)-го приближения производится по формулам:
ìx1k +1 |
= (b1 - a12 x2k - a13 x3k )/ a11 |
ï |
|
ï |
= (b2 - a21x1k - a23 x3k )/ a22 |
íx2k +1 |
|
ï |
= (b3 - a31x1k - a32 x2k )/ a33 |
ïx3k +1 |
|
î |
|
Итерационный процесс продолжается до тех пор, пока не будет вы- полнено условие:
max{D1,D2 ,D3}< ε ,
где D1 = x1k +1 - x1k , D2 = x2k +1 - x2k , D3 = x3k +1 - x3k .
Отметим, что для сходимости метода простых итераций доста-
точно выполнение условия доминирования диагональных элементов системы. Данные условия для системы размерности 3´3 имеют вид:
a11 |
|
³ |
|
a12 |
|
+ |
|
a13 |
|
, |
|
a22 |
|
³ |
|
a21 |
|
+ |
|
a23 |
|
, |
|
a33 |
|
³ |
|
a31 |
|
+ |
|
a32 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
Если указанные условия не соблюдаются (в том числе, если aii = 0 , i = 1, 2, 3 ), их выполнения можно добиться путем применения к урав-
нениям системы элементарных преобразований, таких как: переста- новка строк; умножение любой строки на ненулевой коэффициент и сложение с другой строкой.
Задание 1. Найти решение системы линейных уравнений
ì0,63x1 + 0,05x2 + 0,15x3 = 0,34 ïí0,05x1 + 0,34x2 + 0,1 x3 = 0,32 ïî0,15x1 + 0,1 x2 + 0,7 x3 = 0,72
методом простых итераций с точностью ε=0,001.
Оформить заголовок лабораторной работы, ввести исходные дан- ные – матрицы А и В, заполнить заголовок таблицы (A9:K9, рис. 6.1).
В ячейках А10:С10 задать начальное приближение к решению, для этого установить ссылки на коэффициенты матрицы В (G5:G7). В ячейки А11:С11 ввести формулы метода простых итераций.
Обратите внимание на то, что ссылки на коэффициенты системы должны иметь абсолютную адресацию (используйте клавишу F4).
Заполнить блок вычисления погрешностей D1 , D2 , D3 прибли-
женного решения на (к+1)-ом шаге (D11:F11). Для этого достаточно распространить вправо формулу ячейки D11. С помощью функции «МАКС» определить максимальную из полученных погрешностей
(G11).
С помощью функции «ЕСЛИ» ввести комментарий (Н11), сигна- лизирующий об окончании итерационного процесса. Обратите внима- ние на необходимость применения абсолютной адресации ($I$6) при использовании в формулах ссылок на значение заданной точности ε. Ввести формулы для вывода приближенного решения системы линей- ных уравнений: Х1 (I11), Х2 (J11), Х3 (К11).
Задание 2. Решить индивидуальный вариант (см. таблицу 3 при- ложения). Предварительно проверить выполнение условия доминиро- вания диагональных элементов. Если данное условие не выполняется, преобразовать систему линейных уравнений. Скопировать контроль- ный пример на новый лист и ввести свои данные — матрицы А и В. Получить ответ, оформить работу в тетради.
31
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
4 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
0,63 |
0,05 |
0,15 |
|
|
0,34 |
|
ε |
|
|
6 |
A= |
0,05 |
0,34 |
0,1 |
|
B= |
0,32 |
|
0,001 |
|
|
7 |
|
0,15 |
0,1 |
0,7 |
|
|
0,72 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
9 |
х1(k+1) |
х2(k+1) |
х3(k+1) |
1 |
2 |
3 |
Макс. |
коммент. |
х1 |
х2 |
х3 |
10 |
0,340 |
0,320 |
0,720 |
|
|
|
|
|
|
|
|
11 |
0,343 |
0,679 |
0,910 |
0,003 |
0,359 |
0,190 |
0,359 |
Продолж. |
... |
... |
... |
12 |
0,269 |
0,623 |
0,858 |
0,074 |
0,056 |
0,052 |
0,074 |
Продолж. |
... |
... |
... |
13 |
0,286 |
0,649 |
0,882 |
0,017 |
0,026 |
0,024 |
0,026 |
Продолж. |
... |
... |
... |
14 |
0,278 |
0,640 |
0,875 |
0,008 |
0,009 |
0,007 |
0,009 |
Продолж. |
... |
... |
... |
15 |
0,281 |
0,643 |
0,878 |
0,003 |
0,003 |
0,003 |
0,003 |
Продолж. |
... |
... |
... |
16 |
0,280 |
0,642 |
0,877 |
0,001 |
0,001 |
0,001 |
0,001 |
Продолж. |
... |
... |
... |
17 |
0,280 |
0,642 |
0,877 |
0,000 |
0,000 |
0,000 |
0,000 |
Стоп |
Х1=0,28 |
Х2=0,642 |
Х3=0,877 |
Р и с. 6.1. Решение системы линейных уравнений методом простых итераций

Метод Зейделя. Отличие метода Зейделя от метода простых ите- раций заключается в том, что при вычислении x2k +1 используется зна- чение x1k +1 , полученное на текущей итерации, а при вычислении x3k +1 — значения x1k +1 , x2k +1 :
ìx1k +1 |
= (b1 - a12 x2k - a13 x3k )/ a11 |
ï |
|
ï |
= (b2 - a21x1k +1 - a23 x3k )/ a22 |
íx2k +1 |
|
ï |
= (b3 - a31x1k +1 - a32 x2k +1 )/ a33 |
ïx3k +1 |
|
î |
|
Данная модификация позволяет ускорить сходимость итерационного процесса.
Задание 3. Найти решение системы линейных уравнений
ì0,63x1 + 0,05x2 + 0,15x3 = 0,34 ïí0,05x1 + 0,34x2 + 0,1 x3 = 0,32 ïî0,15x1 + 0,1 x2 + 0,7 x3 = 0,72
методом Зейделя с точностью ε=0,001.
Скопировать лист лабораторной работы, выполненной методом простых итераций. В ячейках А11:С11 записать формулы, реализую- щие метод Зейделя, и распространить их вниз до появления слова «Стоп».
|
A |
B |
C |
D |
E |
F |
G |
8 |
|
|
|
|
|
|
|
9 |
х1(k+1) |
х2(k+1) |
х3(k+1) |
1 |
2 |
3 |
Макс. |
10 |
0,340 |
0,320 |
0,720 |
|
|
|
|
11 |
0,343 |
0,679 |
0,858 |
0,003 |
0,359 |
0,138 |
0,359 |
12 |
0,281 |
0,647 |
0,876 |
0,061 |
0,032 |
0,018 |
0,061 |
13 |
0,280 |
0,642 |
0,877 |
0,002 |
0,005 |
0,001 |
0,005 |
14 |
0,280 |
0,642 |
0,877 |
0,000 |
0,000 |
0,000 |
0,000 |
Р и с. 6.2. Решение системы линейных уравнений методом Зейделя
Очевидно, что решения Х1, Х2, Х3, полученные методом простых итераций и методом Зейделя, должны отличаться на величину не бо-
лее 0,001.
33

Задание 4. Решить индивидуальный вариант (см. таблицу 3 при- ложения) методом Зейделя. Оформить работу в тетради.
Оформите ответ:
Решена система линейных уравнений ______________ с точностью ε=______.
Корни системы X1= _________, X2= _________, X3= _________ найдены на
___ шаге метода простых итераций и на ___ шаге метода Зейделя.
Выше рассмотрены приближенные методы решения систем ли- нейных уравнений.
Запишем исходную систему линейных уравнений в матричной форме:
AX = B .
Для нахождения точного решения системы линейных уравнений мож- но воспользоваться методом обратной матрицы:
X = A−1B .
Следует помнить, что метод обратной матрицы применяется только для решения систем линейных уравнений, содержащих равное
количество уравнений и неизвестных и являющихся невырожденными (определитель A ¹ 0 ).
Задание 5. Выполнить проверку правильности приближенного решения системы линейных уравнений
ì0,63x1 + 0,05x2 + 0,15x3 = 0,34 ïí0,05x1 + 0,34x2 + 0,1 x3 = 0,32 ïî0,15x1 + 0,1 x2 + 0,7 x3 = 0,72,
полученного методами простых итераций и Зейделя, используя метод обратной матрицы.
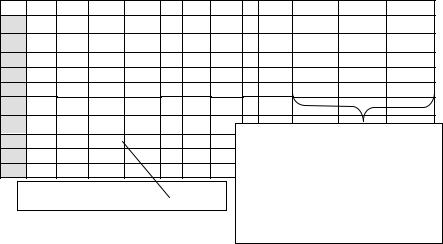
Выполнить контрольный пример (см. рис. 6.3) на отдельном лис- те. Оформить заголовок лабораторной работы, скопировать исходные данные — матрицы А и В.
Средствами Microsoft Excel вычислить матрицу, обратную данной (J5:L7). Найти корни системы путем умножения обратной матрицы (J5:L7) на матрицу В (G5:G7). При заполнении блока С10:С12 ис-
пользуется мастер функций и сочетание клавиш CTRL+SHIFT+ENTER. Сравнить полученные ответы с результатами предыдущих лабораторных работ.
34
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
3
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
0,63 |
0,05 |
0,15 |
|
0,34 |
A-1= |
1,680 |
-0,147 |
-0,339 |
6 |
A= |
0,05 |
0,34 |
0,1 |
B= |
0,32 |
-0,147 |
3,083 |
-0,409 |
|
7 |
|
0,15 |
0,1 |
0,7 |
|
0,72 |
|
-0,339 |
-0,409 |
1,560 |
8 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
Для нахождения обратной |
|||
10 |
|
|
0,280 |
|
|
|
||||
11 |
|
X= |
0,642 |
|
|
|
матрицы: |
|
|
|
12 |
|
|
0,877 |
|
|
|
– выделить диапазон (J5:L7); |
|||
|
=МУМНОЖ(J5:L7;G5:G7) |
|
– набрать =МОБР(B5:D7) |
|||||||
|
|
– вместо OK нажать комби- |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
нацию Ctrl+Shift+Enter |
|||
Р и с. 6.3. Решение системы линейных уравнений методом обратной матрицы
Задание 6. Решить индивидуальный вариант (см. таблицу 3 при- ложения) методом обратной матрицы.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задание 7. 1) С помощью элементарных преобразований добиться выполнения условия доминирования диагональных элементов систе-
мы линейных уравнений
ì2,7x1 + 9,8x2 + 3,3x3 = 2,1 ïí3,5x1 +1,7x2 + 2,8 x3 =1,7 ïî4,5x1 + 5,8 x2 - 2,7x3 = 0,8
2) Решить систему линейных уравнений
ì6x1 + x2 + x3 =12 ïíx1 + 2x2 + x3 = 2 ïî2x1 + x2 - 4x3 = 8
Выполнить два шага: а) методом Зейделя; б) методом итераций.
В качестве начального приближения ( x10 , x20 , x30 ) использовать значе-
ния (0,0,0).
Контрольные вопросы
1.Решение СЛУ методом Зейделя. Сходимость метода.
2.Решение СЛУ методом итераций. Сравнение методов.
35

Приложения
ТРЕНИРОВОЧНЫЙ ТЕСТ
№ |
|
|
|
|
Задания |
Варианты ответов |
||||||
|
|
|
|
|
|
|
|
|
|
|||
1 |
Вычислить абсолютную погрешность функ- |
А. |
0,27 |
В. |
0,5 |
|||||||
|
ции y = ab - a , если a = 3 ± 0,03; b = 6 ± 0,04 . |
С. |
0,30 |
D. |
0,33 |
|||||||
|
|
|
|
|
|
|
|
|
||||
2 |
Найти относительную погрешность функции |
А. |
0,08 |
В. |
0,1, |
|||||||
|
y = a |
b |
, если относительные погрешности |
С. 0,0616 |
D. 0,0012 |
|||||||
|
переменных δa = 0,06; δb = 0,04 . |
|||||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
3 |
Вычислить предельную относительную по- |
А. |
0,005 |
В. |
0,001 |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
грешность функции y = |
|
a + b , если |
|||||||||
|
|
С. |
0,05 |
D. 0,003 |
||||||||
|
A = 2 ± 0,02; B = 4 ± 0,04 . |
|||||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
4 |
Установить, какая из точек может быть на- |
|
|
|
|
|||||||
|
чальной при решении уравнения |
А. |
1), |
В. 2), |
||||||||
|
x3 + 3x2 − 2 = 0 методом касательных: |
С. 3), |
D. 1) и 3). |
|||||||||
|
1) х0= -3; |
2) х0= -2; 3) х0=0. |
|
|
|
|
||||||
5 |
С помощью графического метода найти отре- |
А. [3; 5] |
В. [1; 2] |
|||||||||
|
зок, содержащий корень уравнения |
С. [-2; 0] |
D. [0; 1] |
|||||||||
|
x2 - e− x = 0 . |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
6 |
Выполнить две итерации метода касательных |
А. |
1,5 |
В. |
1,39 |
|||||||
|
для решения уравнения x3 + x = 4 на отрезке |
С. |
0,87 |
D. |
1,7 |
|||||||
|
[1; 2]. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
7 |
Выполнить две итерации методом Зейделя |
|
|
|
|
|||||||
|
для решения системы линейных уравнений |
А. х(2)=(2,8;-0,33;-0,6) |
||||||||||
|
ì5x1 +3x2 + x3 = 10 |
|
|
|
В. х(2)=(2;-1;-1) |
|||||||
|
ï |
− 6x2 |
+ 2x3 = 6 |
|
|
|
С. х(2)=(2,2;-0,23;-1,0) |
|||||
|
í3x1 |
|
|
|
||||||||
|
ï |
+ 4x2 |
-10x3 = 18 |
|
|
|
D. х(2)=(1,8;-0,33;-0,9) |
|||||
|
î4x1 |
|
|
|
|
|
|
|
||||
|
Начальное приближение x(0)=(0; 0; 0). |
|
|
|
|
|||||||
Ответы: 1) А; |
2) А; 3) А; |
4) А; 5) D; 6) В; 7) C. |
|
|
|
|||||||
36

Т е м а 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
Таблица 1
Задания к лабораторной работе № 1
№ |
Выражение |
Значения параметров |
|||||||||||||||||||||||||
п/п |
A |
B |
C |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. |
x = |
|
a ×b |
3,85±0,04 |
2,043±0,004 |
96,6±0,2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 c |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
×b |
|
|
|
|
|||||||||||
2. |
x = |
|
|
|
|
|
a |
2,28±0,6 |
84,6±0,02 |
68,7±0,05 |
|||||||||||||||||
|
|
|
|
|
c |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
x = |
|
|
|
|
|
a ×b |
4,632±0,03 |
23,3±0,04 |
11,3±0,6 |
|||||||||||||||||
|
|
|
|
|
c |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
x = |
a2b |
|
|
|
|
|
|
|
|
0,323±0,005 |
3,147±0,008 |
1,78±0,05 |
||||||||||||||
|
|
c |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
5. |
x = |
ab3 |
|
|
|
|
|
|
|
|
|
0,323±0,005 |
3,147±0,008 |
1,78±0,05 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||||||||||||
6. |
x = |
ab |
|
|
|
|
|
|
|
|
0,258±0,01 |
3,45±0,004 |
1,374±0,007 |
||||||||||||||
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
||||||||||||||||
7. |
x = |
|
a2b |
|
2,712±0,005 |
0,37±0,02 |
13,21±0,08 |
||||||||||||||||||||
c - b |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
8. |
x = |
|
a2b |
3,804±0,003 |
4,05±0,005 |
2,18±0,01 |
|||||||||||||||||||||
|
|
|
c |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
x = |
|
|
|
a ×c |
0,834±0,004 |
138±0,03 |
1,84±0,01 |
|||||||||||||||||||
|
|
|
|
|
|
b |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
10. |
x = |
a - b |
|
|
|
54,8±0,02 |
2,45±0,01 |
0,68±0,04 |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
b ×c |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
x = |
|
|
|
|
a ×b |
13,28±0,02 |
2,37±0,007 |
5,13±0,01 |
||||||||||||||||||
|
|
|
|
c2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x = |
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
12. |
b |
0,231±0,008 |
2,13±0,01 |
5,91±0,05 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
c2 |
|
|
|
||||||||||||||||
13. |
x = |
|
|
|
|
|
|
a |
1,182±0,005 |
2,18±0,009 |
0,19±0,01 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
c + b |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x = |
a + |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
14. |
c |
0,95±0,01 |
2,3±0,03 |
1,195±0,005 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
b2 |
|
|
|
||||||||||||||||
37

|
|
|
|
|
|
|
Окончание табл. 1 |
||
№ |
Выражение |
Значения параметров |
|||||||
п/п |
A |
B |
C |
||||||
x = a + b |
|||||||||
15. |
1,19±0,05 |
2,3±0,1 |
5,191±0,08 |
||||||
|
|
|
|
|
c |
|
|
|
|
16. |
x = |
|
|
a |
13,52±0,02 |
5,1±0,03 |
9,273±0,008 |
||
b |
+ |
c |
|||||||
|
|
|
|
|
|||||
17. |
x = |
|
|
a |
1,18±0,01 |
2,75±0,05 |
3,62±0,007 |
||
|
c |
+ b |
|||||||
|
|
|
|
|
|
||||
18. |
x = a + |
b |
1,95±0,03 |
2,18±0,01 |
9,193±0,008 |
||||
|
|
|
|
|
c |
0,193±0,006 |
1,19±0,01 |
2,276±0,009 |
|
19. |
x = a + b + c2 |
||||||||
20. |
x = a + |
c |
2,56±0,04 |
1,785±0,09 |
3,4±0,1 |
||||
|
|
|
|
|
b |
|
|
|
|
21. |
x = |
|
|
a |
0,171±0,004 |
0,91±0,007 |
1,1±0,01 |
||
b |
+ |
c |
|||||||
|
|
|
|
|
|||||
22. |
x = b + |
a |
1,65±0,06 |
0,09±0,04 |
13,5±0,08 |
||||
c |
|||||||||
23. |
x = |
a + b2 |
1,18±0,05 |
5,1±0,01 |
0,9±0,005 |
||||
|
|
|
|
|
c |
|
|
|
|
24. |
x = |
ac + b |
13,7±0,05 |
6,2±0,01 |
0,721±0,008 |
||||
|
|
|
|
|
a |
|
|
|
|
25. |
x = |
|
|
b |
0,18±0,005 |
1,231±0,008 |
7,3±0,01 |
||
c |
+ |
a |
|||||||
|
|
|
|
|
|||||
26. |
x = a + |
b |
13±0,08 |
7,1±0,02 |
0,831±0,007 |
||||
|
|
|
|
|
с |
|
|
|
|
27. |
x = a |
+ |
c |
15,76±0,03 |
7,3±0,05 |
1,141±0,009 |
|||
|
|
b |
|
|
|
|
|
|
|
28. |
x =1+ |
|
a + b |
0,841±0,008 |
1,13±0,01 |
5,21±0,04 |
|||
|
|
|
|
|
c |
|
|
|
|
29. |
x = a + |
c |
1,692±0,005 |
2,13±0,008 |
13,1±0,02 |
||||
|
|
|
|
b |
|
|
|
||
30. |
x = a3 |
× с |
3,85±0,02 |
2,043±0,005 |
9,61±0,04 |
||||
|
|
|
|
|
b |
|
|
|
|
38 |
|
|
|
|
|
|
|
|
|

Т е м а 2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Таблица 2
Задания к лабораторным работам № 2—5
№ |
Уравнение |
№ |
Уравнение |
|||||||||||
п/п |
п/п |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
x3 - 3x2 + 3 = 0 |
16. |
2 - x = ln (x) |
|||||||||||
2. |
x + 2 = e2 x |
17. |
x + lg (x) = 0,5 |
|||||||||||
3. |
x3 + 3x2 - 2 = 0 |
18. |
(x +1)2 = |
1 |
|
e−x |
||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
3x + cos(x) +1 = 0 |
19. |
(2 - x)ex |
= 1 |
||||||||||
5. |
x3 -12x - 5 = 0 |
20. |
x2 + 4sin (x) +1 = 0 |
|||||||||||
6. |
(x +1)3 + ln (x) = 0 |
21. |
4cos(x) − 2x3 = 0 |
|||||||||||
7. |
x ×2x = 1 |
22. |
x3 + 6x2 - 5 = 0 |
|||||||||||
8. |
|
|
|
|
= x |
23. |
2cos 2x − 3x = 0 |
|||||||
|
x +1 |
|||||||||||||
9. |
x - cos(x) = 0 |
24. |
x3 + 3e2x |
= 0 |
||||||||||
10. |
x + ln |
x |
= 0 |
25. |
|
|
= 2x |
|||||||
|
x +1 |
|||||||||||||
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||
11. |
2x3 + 9x2 − 4 = 0 |
26. |
x2 − 3e−2x |
= 0 |
||||||||||
12. |
x3 + 3x2 −1 = 0 |
27. |
x3 + 2sin (3x) + 2 = 0 |
|||||||||||
13. |
x3 + cos(x) = 0 |
28. |
cos(x) − x + 2 = 0 |
|||||||||||
14. |
x3 − 3x2 + 3,5 = 0 |
29. |
(x −1)2 − e−(x+1) = 0 |
|||||||||||
15. |
x3 +12x2 −10 = 0 |
30. |
(x −1)2 = |
|
1 |
ex |
||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
39
