3. Вспомогательная теорема

Пусть имеются два метрических пространства: Y (с элементами у) и F (с элементами f).

Пусть определен оператор А, который каждому элементу ставит в соответствие элемент и одновременно однозначно определен обратный оператор , т.е. закон соответствия .

Замечание. Обратный оператор определен, вообще говоря, не на всем множестве F, а лишь на его части, на подмножестве F, элементы которого определяются по закону .

Определение. Последовательность называется сходящейся в метрике пространства Y к некоторому элементу если ρ_Y(при n∞.

Определение. Последовательность называется компактной в Y, если из каждого бесконечного подмножества ее элементов можно выделить подпоследовательность, сходящуюся к некоторому элементу .

Определение. Оператор А, переводящий элемент элемент , называется непрерывным, если какова бы ни была последовательность , сходящаяся в Y к у, соответствующая последовательность сходится в F к f=Ау.

Теорема 1. Пусть в пространстве Y имеется последовательность , которой в пространстве F отвечает последовательность . Пусть , A является непрерывным оператором, а последовательность является компактной. Тогда

4. Алгоритм построения приближенного решения

Будем считать, что решение задачи (2.1) существует при некоторой фиксированной функции , и обозначим его . Ядро будем считать непрерывным и замкнутым, что обеспечивает единственность решения.

Пользуясь теоремой 1, построим последовательность функций, позволяющую получить с любой степенью точности решения некорректной задачи (2.1) по приближенно заданной функции .

Приближенное задание функции 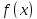будем понимать как задание последовательности непрерывных на [с, d] функций таких, что где — некоторая числовая последовательность. Таким образом, аппроксимирует даже не обязательно равномерно, а в смысле среднего квадратичного.

Алгоритм построения приближенного решения уравнения (2.1) по заданной последовательности состоит в том, что выбирается некоторая числовая последовательность , где — не зависящая от n постоянная, и для каждого находится функция , реализующая минимальное значение сглаживающего функционала . Так как теперь мы специально интересуемся зависимостью у от , то будем эту зависимость указывать верхним индексом. Равенство означает, что параметр регуляризации согласован с точностью задания .

Оказывается, при достаточно большом n функция обеспечивает равномерное приближение к с произвольной степенью точности, что можно выразить следующей теоремой:

Теорема 2. Пусть — решение уравнения (2.1). Пусть — последовательность непрерывных функций, являющихся приближениями для так, что

где при . Пусть функция реализует минимальное значение сглаживающего функционала , где ( не зависит от n). Тогда для найдется такое, что при справедливо неравенство

(2)

5. Численное решение уравнение Фредгольма первого рода

Рассмотрим уравнение : (5.1)

с замкнутым ядром . Как было показано уравнение Фредгольма первого родя является некорректно поставленной задачей. Малые возмущения функции , неизбежные, например, при экспериментальном определении этой функции или даже при округлении чисел в процессе счета на компьютере, могут приводить к существенным изменениям функции или к тому, что решения уравнения вообще не существует. Как было показано, в этом случае следует использовать методы регуляризации. Метод регуляризации рекомендует в качестве приближенного решения использовать функцию , реализующую минимальное значение сглаживающего функционала

(5.2)

При применении метода регуляризации α и как находить при заданном α?

1. Определение при заданном α. При фиксированном значении α функция может быть определена двумя способами:

1. методами минимизации функционала , например, методом скорейшего спуска, методом сопряженных градиентов и др.;

2. решением краевой интегро-дифференциальной задачи определяющей экстремали функционала (5.2).

Замечание. Если на функцию в задаче (5.1) накладываются дополнительные ограничения, например, требование, чтобы не выходило за пределы определенной области, то применяется лишь первый способ.

Задачу (5.2), вообще говоря, приходится решать приближенно с использованием конечно-разностной аппроксимации. Мы рассмотрим простейший случай p=q=1. Решение строим в области 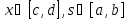. Вводим равномерную сетку по x и по s. Узлы сетки по . Узлы сетки по . Шаг сетки по х равен , шаг сетки по s равен . Тогда функционалу будет соответствовать сумма

, (5.3)

где

. Величина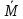 зависит от выбора . Минимальное значение достигается при , определяемых из условия

. (5.4)

Для удобства записи введем два числа: и , считая , а . Тогда, вычисляя производные 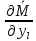из (5.3) и приравнивая из согласно (5.4) нулю, получаем

(5.5)

где

, .

Полученная задача (5.5) представляет собой разностную схему, соответствующую задаче (2.10), (2.6). Эта схема имеет порядок аппроксимации 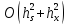. Соотношения (5.5) являются системой алгебраических уравнений и могут быть решены, например, методом исключения Гаусса.

2. Выбор параметра регуляризации α. Пусть решается уравнение (5.1), причем точное значение функции f неизвестно, но задана функция и оценка погрешности δ такие, что , а . Пусть - функция, реализующая минимальное значение сглаживающего функционала при значении параметра реализации α. Если выбрать α слишком малым, то в выражении (2.6) влияние регуляризующего слагаемого будет малым и решение окажется «сильно разболтанным». Если же α выбрать чересчур большим, то, наоборот, решение окажется «заглаженным».

Проиллюстрируем сказанное на примере интегрального уравнение

(5.6)

Где . Ядро подобного типа встречается в задачах гравиметрии.

Положим . Тогда из (5.6) можно вычислить f(x) с заданной степенью точности, например, δ=0,001. Попытаемся теперь, располагая приближенным значением f(x), восстановить y(x), т.е. решить интегральное уравнение Фредгольма первого рода.

На рис.1 представлены результаты расчета, которые получаются непосредственным применением конечно-разностного метода без регуляризации. Использовалась разностная схема

(5.7)

Сплошная кривая на рисунке представляет собой график точного решения . Числа, помеченные возле вертикальных линий, представляют собой значения , вычисленные из алгебраических уравнений (5.7). Как видно, эти значения сильно разбросаны и отвечающие им точки даже не умещаются в пределах чертежа, что отмечено стрелками. Эти точки не имеют ничего общего с графиком кривой , которую, как можно заключить, получить описанным путем не удается.

Рис. 1

На рис. 4 представлен результат решения той же задачи с применением метода регуляризации. На этом чертеже сплошная кривая снова означает график решения . Кривые I, II и III получены в результате выбора и соответственно.

Рис. 2

При этом видно, что кривая II в пределах точности чертежа совпадает с графиком точного решения. В случае I параметр α оказался чересчур большим, а в случае III – чересчур малым.

Чтобы избежать обеих нежелательных крайностей в выборе α, целесообразно использовать так называемый принцип невязки. А именно, рассмотрим функцию

, (5.8)

которая называется невязкой. Имеет место следующее утверждение: δ(α) при α>0 является монотонно возрастающей дифференцируемой функцией α. При этом . Следовательно, уравнение ρ(α)=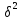 имеет единственный корень . Это значение α и следует выбирать в качестве регуляризации.

Итак, рассматриваемый алгоритм регуляризации состоит в том, что численными метода (например, методом Ньютона) ищется корень уравнения 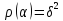. При этом величина при нужных значениях α вычисляется согласно (5.8), где - функция, реализующая минимум .

Список использованной литературы

1. Методы решения некорректных задач. Тихонов А. Н., Арсенин В. Я. М.: Наука. Главная редакция физико-математической литературы, 1979. Изд. 2-е.

2. Интегральные уравнения. Васильева А. Б., Тихонов А. Н. – 2-е изд., стереот. – М.: ФИЗМАТЛИТ, 2002.