
ГБОУ ВПО
«СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Ханты-Мансийского автономного округа - Югры»
Кафедра автоматизированных систем обработки информации и управления
Реферат
на тему: «Численная реализация приближенного решения уравнения Фредгольма»
Выполнил: студент гр. 1192
Волков Александр Дмитриевич
Проверил: д.ф-м. н. профессор
Галкин Валерий Алексеевич
Сургут, 2013.
Содержание
1.Пример некорректой задачи 3
2.Сглаживающий функционал и его свойства 6
3.Вспомогательная теорема 10
4.Алгоритм построения приближенного решения 11
5.Численное решение уравнение Фредгольма первого рода 13
Список использованной литературы 17
Решение всякой количественной математической задачи обычно заключается в нахождении "решения" y по заданным "исходным данным" f. Запишем это в форме y=R(f), где R — некоторые оператор. Будем считать у и f элементами метрических пространств Y и F с расстояниями между элементами ρY(y1,y2) и ρF(f1,f2).
Определение. Решение у называется
устойчивым, если для любого ε > 0 можно
указать такое δ(ε) > О, что из неравенства
(f1,f2)≤
δ(ε) следует ρY(y1,y2)≤ε,
где f1 и f2
— произвольные элементы F, у1=
R(f2)
 Y,
y2= R(f2)
Y,
y2= R(f2)
 Y.
Y.
Определение. Задача y=R(f) называется корректно поставленной на паре метрических пространств (Y, F), если выполняются условия:
-
Для всякого элемента f
 F
существует решение y
F
существует решение y Y.
Y.
-
Решение определяется однозначно.
-
Решение устойчиво.
Задачи, не удовлетворяющие перечисленным требованиям, называются некорректно поставленными.
Замечание. Метрики в пространствах Y и F характеризуют, в каком смысле понимается малое изменение y и f. От того, каким образом выбрана метрика, может зависеть, будет ли решение у устойчиво при изменении f или нет, а следовательно, будет ли задача y=R(f) корректна.
Следует отметить, что определение некорректно поставленных задач относится к данной паре метрических пространств (Y, F), так как в других метриках та же задача может быть корректно поставленной.
-
Пример некорректой задачи
Задача решения уравнения Фредгольма первого рода:
 (1.1)
(1.1)
Пусть ядро интегрального оператора
K(x,s)
- функция, непрерывная по совокупности
аргументов x∈[c,d],
s∈[a,b],
а решение z(s)
- непрерывная на отрезке [a,b]
функция. Тем самым, можно рассматривать
оператор A как действующий
в следующих пространствах: A:C[a,b]→C[c,d]
(Пространство C[a,b]
состоит из функций, непрерывных на
отрезке [a,b].
Норма z∈C[a,b]
определяется как ||z||= Покажем, что в этом случае задача решения
интегрального уравнения является
некорректно поставленной. Для этого
нужно проверить условия корректности
постановки задачи:
Покажем, что в этом случае задача решения
интегрального уравнения является
некорректно поставленной. Для этого
нужно проверить условия корректности
постановки задачи:
-
Существование решения для любой непрерывной на [c,d] функции u(x). На самом же деле, это не так: существует бесконечно много непрерывных функций, для которых решения нет.
-
Единственность решения. Это условие выполняется в том и только в том случае, если ядро интегрального оператора замкнуто.
Первые два условия корректности эквивалентны условию существования обратного оператора A-1 с областью определения D(A−1)=C[c,d]. Если ядро интегрального оператора замкнуто, то обратный оператор существует, однако область его определения не совпадает с C[c,d]
-
Устойчивость решения. Это означает, что для любой последовательности
 последовательность zn→
последовательность zn→ .
Устойчивость эквивалентна непрерывности
обратного оператора
.
Устойчивость эквивалентна непрерывности
обратного оператора
 при условии, что обратный оператор
существует. В данном случае это не так,
что видно из следующего примера. Пусть
последовательность непрерывных функций
при условии, что обратный оператор
существует. В данном случае это не так,
что видно из следующего примера. Пусть
последовательность непрерывных функций
 , n=1, 2, …, такая что
, n=1, 2, …, такая что
 на промежутке
на промежутке
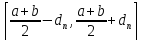 и обращается в нуль вне данного интервала,
max|z(s)|=1, s∈[a, b], а
последовательность чисел d→0+0.Такая
функция может быть выбрана, например,
кусочно-линейной. Тогда для любого x
∈[c, d]
и обращается в нуль вне данного интервала,
max|z(s)|=1, s∈[a, b], а
последовательность чисел d→0+0.Такая
функция может быть выбрана, например,
кусочно-линейной. Тогда для любого x
∈[c, d]

при

Последовательность функций
 равномерно, т.е. по норме C[c,d], сходится
к
равномерно, т.е. по норме C[c,d], сходится
к
 =0.
Хотя решение уравнения
=0.
Хотя решение уравнения
 в этом случае
в этом случае
 =0,
последовательность
=0,
последовательность
 не стремится к
не стремится к
 ,
так как
,
так как .
.
Интегральный оператор A является вполне
непрерывным при действии из
 в
в
 ,
при действии из C[a,b] в
,
при действии из C[a,b] в
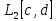 и при действии из C[a,b] в C[c,d]. (Пространство
и при действии из C[a,b] в C[c,d]. (Пространство
 состоит из функций, интегрируемых с
квадратом на отрезке [a,b]. Норма z∈
состоит из функций, интегрируемых с
квадратом на отрезке [a,b]. Норма z∈ определяется как
определяется как
 ). Это означает, что любую ограниченную
последовательность этот оператор
преобразует в компактную. Компактная
последовательность по определению
обладает тем свойством, что из любой ее
подпоследовательности можно выделить
сходящуюся. Легко указать последовательность
). Это означает, что любую ограниченную
последовательность этот оператор
преобразует в компактную. Компактная
последовательность по определению
обладает тем свойством, что из любой ее
подпоследовательности можно выделить
сходящуюся. Легко указать последовательность
 ,
,
 ,
из которой нельзя выделить сходящуюся
в C[a,b] подпоследовательность. Например,
,
из которой нельзя выделить сходящуюся
в C[a,b] подпоследовательность. Например,

Нормы всех членов этой последовательности
равны 1 в
 ,
но из любой подпоследовательности этой
последовательности нельзя выделить
сходящуюся, поскольку
,
но из любой подпоследовательности этой
последовательности нельзя выделить
сходящуюся, поскольку
 .
Очевидно, что эта последовательность
состоит из непрерывных на [a,b] функций
и равномерно (по норме C[a,b]) ограничена,
но из этой последовательности нельзя
выделить сходящуюся в C[a,b] подпоследовательность
(тогда она сходилась бы и в
.
Очевидно, что эта последовательность
состоит из непрерывных на [a,b] функций
и равномерно (по норме C[a,b]) ограничена,
но из этой последовательности нельзя
выделить сходящуюся в C[a,b] подпоследовательность
(тогда она сходилась бы и в
 ,
поскольку из равномерной сходимости
следует сходимость в среднем). Если
предположить, что оператор
,
поскольку из равномерной сходимости
следует сходимость в среднем). Если
предположить, что оператор
 является непрерывным, то легко прийти
к противоречию. Для существования
обратного оператора достаточно
потребовать, чтобы прямой оператор A
был инъективным. Очевидно, что, если
оператор B: C[c,d]→C[a,b] непрерывный, а
оператор A вполне непрерывный, то BA
:C[a,b] →C[a,b] - тоже вполне непрерывный
оператор. Но тогда, поскольку для любого
n
является непрерывным, то легко прийти
к противоречию. Для существования
обратного оператора достаточно
потребовать, чтобы прямой оператор A
был инъективным. Очевидно, что, если
оператор B: C[c,d]→C[a,b] непрерывный, а
оператор A вполне непрерывный, то BA
:C[a,b] →C[a,b] - тоже вполне непрерывный
оператор. Но тогда, поскольку для любого
n
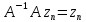 ,
то последовательность
,
то последовательность
 компактна, что неверно. Оператор, обратный
к вполне непрерывному оператору, не
может быть непрерывным. Аналогичное
доказательство может быть проведено
для любых бесконечномерных банаховых
(т.е. полных нормированных) пространств.
компактна, что неверно. Оператор, обратный
к вполне непрерывному оператору, не
может быть непрерывным. Аналогичное
доказательство может быть проведено
для любых бесконечномерных банаховых
(т.е. полных нормированных) пространств.
Поскольку задача решения интегрального уравнения Фредгольма первого рода в указанных пространствах некорректно поставлена, то даже при очень малых ошибках в задании u(x) решение может либо отсутствовать, либо как угодно сильно отличаться от искомого точного решения.
