
- •Гоу впо «Сургутский государственный университет Ханты-Мансийского автономного округа-Югра»
- •Часть 1
- •Общие рекомендации студенту-заочнику по работе над курсом высшей математики.
- •Распределение заданий по вариантам.
- •2. Программа дисциплины “математический анализ” (часть I).
- •Введение в математический анализ.
- •Дифференциальное исчисление функции одной переменной.
- •Задачи для контрольных работ Контрольная работа №1 введение в математический анализ
- •Контрольная работа №3
- •Вопросы для самопроверки.
- •Введение в математический анализ.
- •Дифференциальное исчисление функции одной переменной.
- •5. Литература
- •Содержание
Распределение заданий по вариантам.
|
Вариант |
Номера задач контрольных заданий | ||
|
Контрольная работа № 1 |
Контрольная работа № 2 |
| |
|
1 |
1,11,21 |
31,41,51,61, 71,81,91 | |
|
2 |
2,12,22 |
32,42,52,62, 72,82,92 | |
|
3 |
3,13,23 |
33,43,53,63, 73,83,93 | |
|
4 |
4,14,24 |
34,44,54,64, 74,84,94 | |
|
5 |
5,15,25 |
35,45,55,65, 75,85,95 | |
|
6 |
6,16,26 |
36,46,56,66, 76,86,96 | |
|
7 |
7,17,27 |
37,47,57,67, 77,87,97 | |
|
8 |
8,18,28 |
38,48,58,68, 78,88,98 | |
|
9 |
9,19,29 |
39,49,59,69, 79,89,99 | |
|
0 |
10,20,30 |
40,50,60,70, 80,90,100 | |
ЗАЧЕТЫ И ЭКЗАМЕНЫ
После каждого семестра студент должен сдавать зачет или экзамен. Обычно экзамену или зачету предшествует собеседование студента с преподавателем по выполненным контрольным работам.
На зачете и экзамене от студента требуется знание определений, формулировок и доказательств теорем в объеме программы курса, знание формул и умение решать соответствующие задачи. При подготовке к экзамену рекомендуется повторить учебный материал по учебнику и конспекту.
2. Программа дисциплины “математический анализ” (часть I).
Введение в математический анализ.
Элементы теории множеств и математической логики: понятие множества, операции над множествами, множество действительных чисел, необходимое и достаточное условия, прямая и обратная теоремы, символы математической логики и их использование.
Абсолютная величина действительного числа и ее свойства.
Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики.
Числовая последовательность и ее предел. Ограниченная переменная.
Бесконечно большие и бесконечно малые величины, их свойства.
Теоремы о пределах. Признаки существования предела переменной.
Предел функции в точке. Два замечательных предела.
Неопределенности и их раскрытие.
Сравнение бесконечно малых.
Непрерывность функции в точке. Разрывы функции.
Сложная функция и ее непрерывность. Непрерывность элементарных функций.
Свойства функций, непрерывных на отрезке.
Дифференциальное исчисление функции одной переменной.
Производная функции в точке. Определение, ее геометрический и механический смысл. Необходимое условие дифференцируемости.
Производные сложной и обратной функций. Формулы и правила дифференцирования.
Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала. Применение дифференциала к приближенным вычислениям.
Производные и дифференциалы высших порядков.
Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Каши. Формулировки и доказательства.
Правило Лопиталя
Исследование функций и построение графиков.
![]()
Задачи для контрольных работ Контрольная работа №1 введение в математический анализ
Найти пределы, не пользуясь правилом Лопиталя.
1.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]()
2.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
3.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)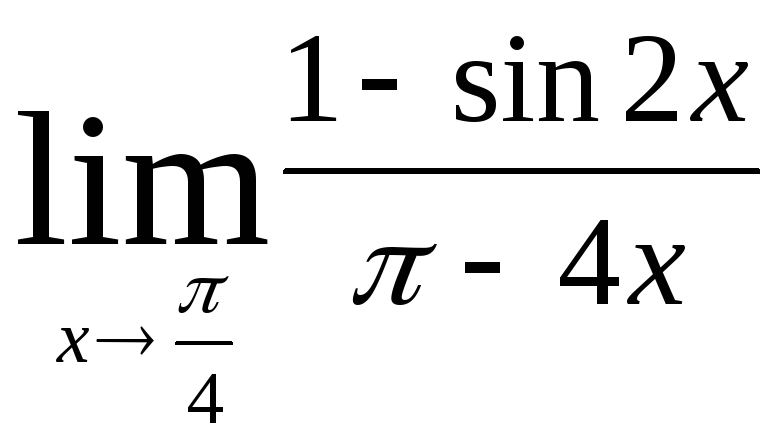 ;
е)
;
е)![]() .
.
4.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
5.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
6.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
7.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
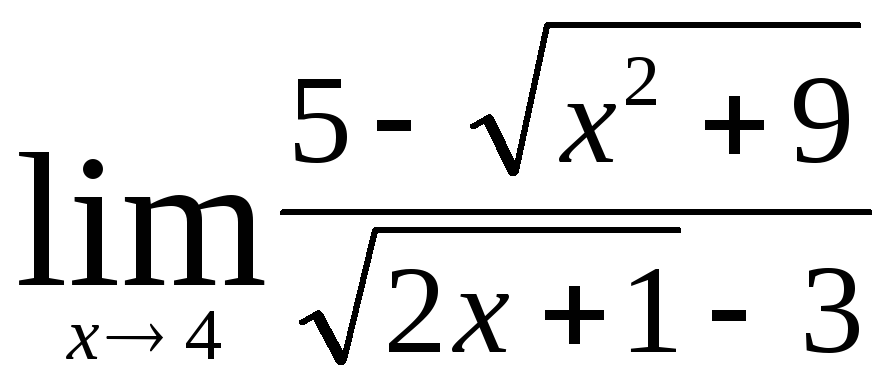 ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
8.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
9.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
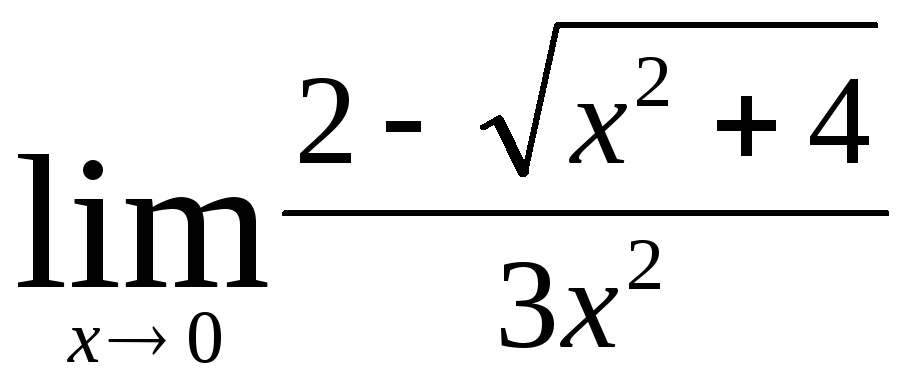 ;
д)
;
д)![]() ;e)
;e)![]()
10.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ; е)
; е)![]() .
.
11-20. Исследовать функцию на непрерывность в указанных точках.
11.
![]() ;
х1
= 1, х2
= 2.
;
х1
= 1, х2
= 2.
12.
![]() ;
х1
= 2, х2
= 3.
;
х1
= 2, х2
= 3.
13.
![]() ;
х1
= 2, х2
= 4.
;
х1
= 2, х2
= 4.
14.
![]() ;
х1
= - 2, х2
= -1.
;
х1
= - 2, х2
= -1.
15.
![]() ;
х1
= -3, х2
= -2.
;
х1
= -3, х2
= -2.
16.
![]() ;
х1
= -3, х2
= -2.
;
х1
= -3, х2
= -2.
17.
![]() ;
х1
= 2, х2
= 4.
;
х1
= 2, х2
= 4.
18.
![]() ;
х1
= 1, х2
= 2.
;
х1
= 1, х2
= 2.
19.
![]() ;
х1
= -5, х2
= -4.
;
х1
= -5, х2
= -4.
20.
![]() ;
х1
= 4, х2
= 5.
;
х1
= 4, х2
= 5.
21-30. Исследовать на непрерывность функцию, найти точки разрыва, указать характер разрыва и построить график функции y = f (x) в области определения.
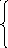 –2x
+ 1 при –2
x
–1,
–2x
+ 1 при –2
x
–1,
21.
f(x)
=
![]() при –1 < x
1,
при –1 < x
1,
2x при 1 < x 2 .
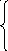
–x 2 при –2 x –1,
22.
f(x)
=
![]() при
–1 < x
1,
при
–1 < x
1,
3 x–1 при 1 < x 2.
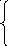 2 x
2
при –2
x
0,
2 x
2
при –2
x
0,
23.
f(x)
=
![]() при 0 < x
2,
при 0 < x
2,
1 при 2 < x 3.
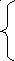 –x
–2 при –2
x
–1,
–x
–2 при –2
x
–1,
24.
f(x)
=
![]() при –1 < x
1,
при –1 < x
1,
ln x при 1 < x e.
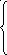 –x
2
при –2
x
–1,
–x
2
при –2
x
–1,
25.
f(x)
=
![]() при
–1 < x
при
–1 < x ![]() ,
,
2 sin
x![]() при
при
![]() <
x
<
x
![]() .
.
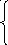 –x–
2 при –3
x
–1,
–x–
2 при –3
x
–1,
26.
f(x)
=
![]() при –1 < x
2,
при –1 < x
2,
1 при 2 < x 3.
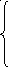
![]() при –1
x
0,
при –1
x
0,
27.
f(x)
=
![]() при 0 < x
1,
при 0 < x
1,
![]() при 1 < x
3.
при 1 < x
3.
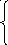
![]() при –2
x
0,
при –2
x
0,
28. f(x) = 2x2–1 4 при 0 < x 1,
1 при 1 < x 3.
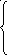 2x2
–1 при –1
x
0,
2x2
–1 при –1
x
0,
29.
f(x)
=
![]() при
0 < x
2,
при
0 < x
2,
x–1 при 2 < x 3.
 cos
x
при –
cos
x
при –![]()
x<
0,
x<
0,
30.
f(x)
=
![]() при 0
< x
2,
при 0
< x
2,
x + 1 при 2 < x 3.
