
- •Глава 1. Основные задачи математической статистики. Выборки и их характеристики.
- •§ 1. Предмет и задачи математической статистики.
- •§ 2. Генеральная и выборочная совокупность. Способы отбора.
- •§ 3. Статистическое распределение выборки.
- •§ 4. Полигон и гистограмма.
- •§ 5 Эмпирическая функция распределения.
- •§ 6. Числовые характеристики статистического распределения выборки.
- •§ 7. Числовые характеристики генеральной совокупности.
- •Глава 2.
- •§1 Понятие о статистических оценках параметров распределения.
- •§2. Точечные и интервальные оценки. Доверительный интервал. Точность оценки. Доверительная вероятность (надежность).
- •§3. Несмещенные, состоятельные и эффективные оценки.
- •§ 4. Точечная оценка генерального среднего по выборочной средней.
- •§ 5. Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии.
- •§6. Метод моментов для точечной оценки параметра распределения.
- •Глава 3.
- •§1. Статистическая гипотеза. Основные понятия.
- •§2. Ошибки первого и второго рода.
- •§ 3. Статистический критерий. Критическая область. Область принятия гипотезы. Критические точки.
- •§ 4. Уровень значимости и мощность критерия.
- •§ 5. Виды критических областей.
- •§6. Методика проверки гипотезы.
- •§ 7. Некоторые типичные задачи проверки параметрических гипотез.
- •7.1 Проверка гипотез о среднем значении.
- •7.2 Сравнение дисперсий 2-ух совокупностей.
- •§ 8. Непараметрические гипотезы. Критерии согласия Пирсона и Колмогорова.
- •8.1 Критерий Пирсона.
- •Глава 4.
- •§ 1. Основные понятия.
- •§ 2. Элементы теории корреляции. Анализ парных связей.
- •§ 3. Оценка показателя связи по выборочным данным. Корреляционное поле.
- •§ 4. Анализ коэффициента корреляции.
- •4.1 Точечная оценка коэффициента корреляции.
- •4.2 Интервальная оценка коэффициента корреляции и проверка значимости.
- •§ 5. Регрессионный анализ. Условные средние. Выборочные уравнения регрессии.
- •§ 6. Корреляционная таблица. Выборочные линии регрессии.
- •§ 7. Линейная регрессия. Выборочный коэффициент корреляции.
- •Глава 5. Основы дисперсионного анализа.
- •§ 1. Исходные понятия.
- •§ 2. Групповое и общее среднее. Групповая, внутригрупповая, межгрупповая и общая дисперсии.
- •§ 3. Однофакторный анализ при полностью случайном плане эксперимента.
- •§ 4. Двухфакторный анализ. (При полностью случайном плане экспериментов.)
§ 3. Статистическое распределение выборки.
Пусть из генеральной
совокупности извлечена выборка и
производятся наблюдения за случайной
величиной
![]() (признак),
причем значение
(признак),
причем значение![]() наблюдалось
наблюдалось![]() -раз,
значение
-раз,
значение![]() наблюдалось
наблюдалось![]() -раза,
-раза,![]() –
–
![]() -раз
и т.д.
-раз
и т.д.
![]()
Возможные значения
случайной величины![]() ,
,![]() ,
,![]() ,….
,….![]() ,
принято
называть вариантами,
а
последовательность вариант, записанную
в порядке возрастания - вариационным
рядом.
,
принято
называть вариантами,
а
последовательность вариант, записанную
в порядке возрастания - вариационным
рядом.
Числа![]() ,
,![]() ,…
,…![]() называют
частотами.
называют
частотами.
![]() где
где
![]() -
относительная частота.
-
относительная частота.
![]()
Перечень вариант и соответствующих им частот (или относительных частот) называется статистическим распределением выборки (или статистическим рядом). Обычно статистический ряд записывают в виде таблицы.
§ 4. Полигон и гистограмма.
Для наглядности часто используют графическое изображение статистических рядов:
для дискретного ряда – полигон;
для интервального ряда – гистограмма.
Полигон частот
(относительных частот), есть ломанная,
отрезки которой соединяют точки (![]() ),
(
),
(![]() ),…..(
),…..(![]() )
или (
)
или (![]() ),(
),(![]() )….(
)….(![]() ).
).
Гистограмма
частот (![]() )
есть ступенчатая фигура, состоящая из
прямоугольников, основаниями которых
служат частичные интервалы длиной
)
есть ступенчатая фигура, состоящая из
прямоугольников, основаниями которых
служат частичные интервалы длиной
![]() и высотами
и высотами
![]() или
или
![]() .
.
Площадь всей гистограммы частот равна n (объем выборки).
Площадь всей гистограммы относительных частот равна 1.
§ 5 Эмпирическая функция распределения.
Пусть задано
статистическое распределение случайной
величины
![]() .
.
Обозначим через
![]() -
число вариант,
меньших
-
число вариант,
меньших
![]() .
.
![]() - любое действительное
число.
- любое действительное
число.
![]() -
объем выборки.
-
объем выборки.
Относительная
частота событий {Х<x}=![]() .
.
При изменении
![]() меняется и относительная частота, т.е
отношение
меняется и относительная частота, т.е
отношение
![]() является функцией отх.
является функцией отх.
Поскольку данная функция строится по данным опыта, то она называется эмпирической.
Эмпирической
функцией распределения (функцией
распределения выборки F*(x))
называется относительная частота
события
![]() ,
где
,
где![]() -
число вариант меньших
x,
n-
объем выборки.
-
число вариант меньших
x,
n-
объем выборки.
![]()
Теоретической
функцией распределения называется
функция распределения F(![]() )
случайной величины
)
случайной величины![]() ,
вычисленная по генеральной совокупности,
т.е вероятность события
,
вычисленная по генеральной совокупности,
т.е вероятность события![]() .
.
Теорема.
При неограниченном возрастании объема выборки эмпирическая функция распределения сходится по вероятности к теоретической функции распределения.
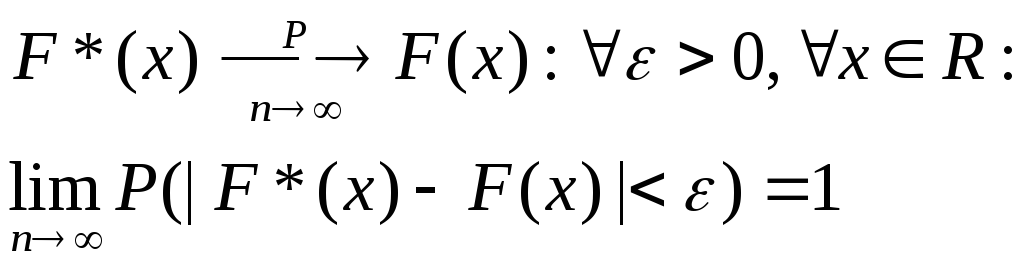
§ 6. Числовые характеристики статистического распределения выборки.
Пусть имеется генеральная совокупность выборки объема N ,из которой сделана выборка объема n.
Статистический
ряд, в котором присутствуют значения
случайной величины X
и относительные частоты их появления,
можно рассматривать как закон распределения
новой случайной величины
![]() ,
а исходную случайную величину –
,
а исходную случайную величину –![]() .
.
Очевидно, что
законы распределения этих величин в
какой-то мере близки, но не совпадают.
Каждой числовой характеристике случайной
величины
![]() соответствует
её выборочный аналог- характеристика
случайной величины
соответствует
её выборочный аналог- характеристика
случайной величины
![]() .
.
При возрастании
объема выборки (![]() ),
числовые характеристики случайной
величины
),
числовые характеристики случайной
величины![]() (СВХ)
будут сходиться по вероятности к
соответствующим характеристикам
(СВХ)
будут сходиться по вероятности к
соответствующим характеристикам
![]() .
.
Наиболее употребительны следующие числовые характеристики выборки:
Выборочное среднее (
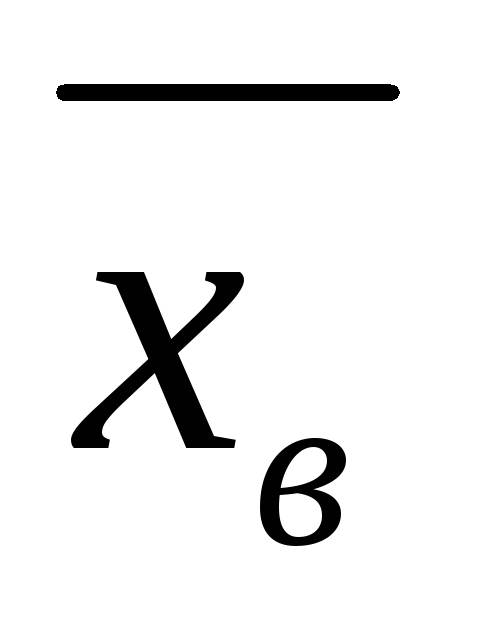 )-среднее
арифметическое значений выборки:
)-среднее
арифметическое значений выборки:
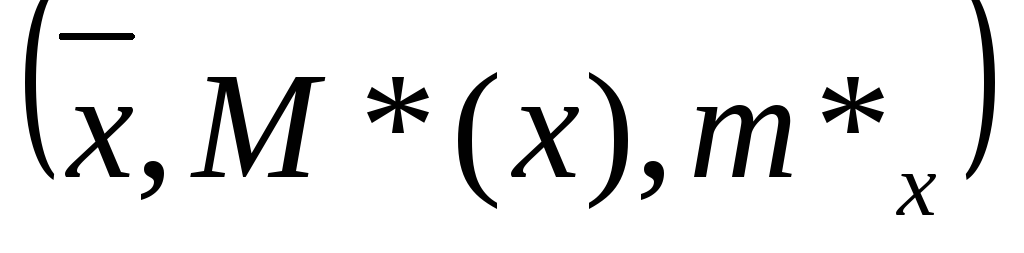 ;
;
Выборочная мода (
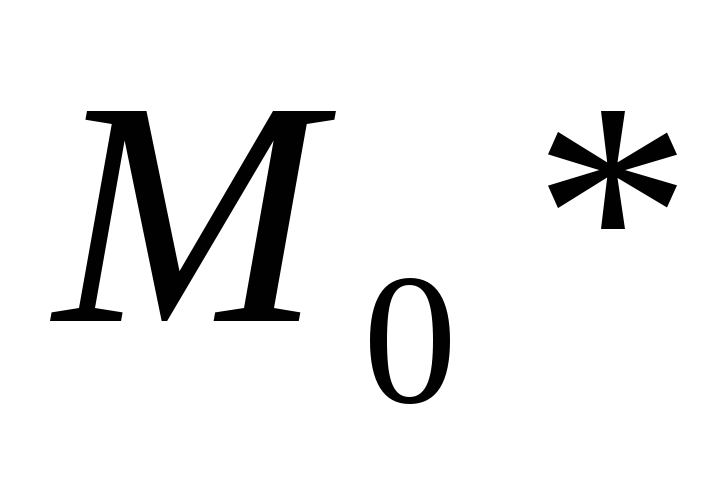 )-
наиболее вероятное значение в выборке
(варианта с наибольшей частотой);
)-
наиболее вероятное значение в выборке
(варианта с наибольшей частотой);Выборочная медиана (
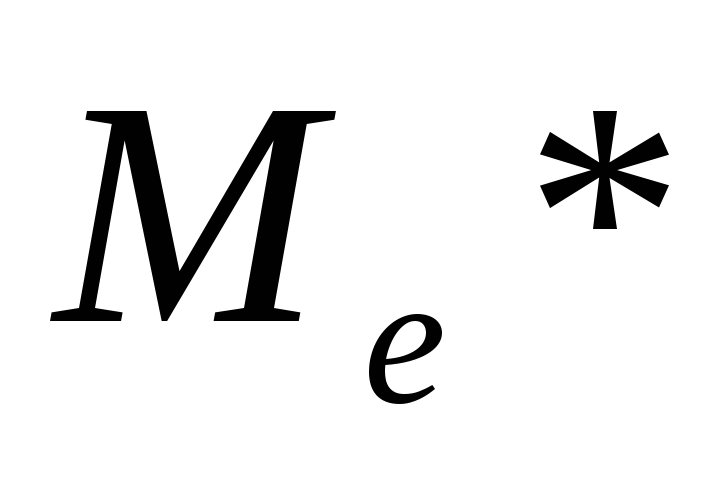 )
- значение случайной величины, приходящейся
на середину вариационного ряда;
)
- значение случайной величины, приходящейся
на середину вариационного ряда;
а) если объем
выборки четный, то
![]()
![]() ;
;
![]()
![]() ;
;
б) если объем
выборки нечетный, то
![]() ;
;
![]() ;
;
В теории вероятности
медиана определяется:![]() .
.
4. Выборочная
дисперсия
- средние значение квадрата отклонения
![]() от
от
выборочной средней
![]()
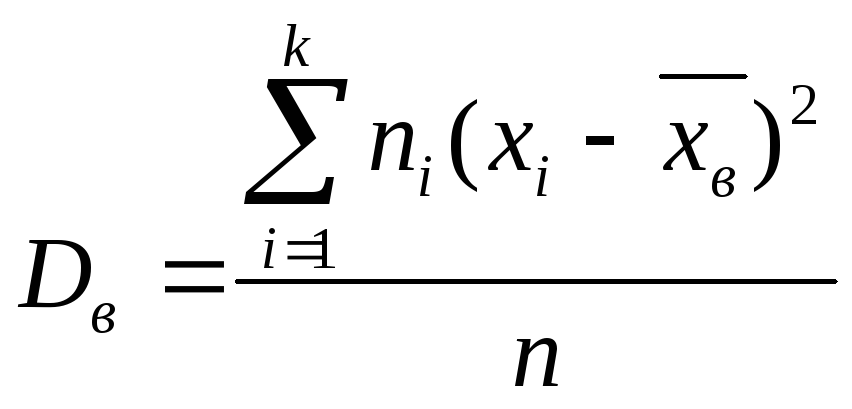 ;
;
5. Выборочное среднее квадратичное отклонение:
![]() ;
;
6. Исправленная выборочная дисперсия:
![]() ;
;
7. Исправленное среднее квадратичное отклонение:
![]() ;
;
Для интервального
статистического ряда все вышеприведенные
формулы сохраняются, но в качестве
значений вариант берутся середины
соответствующих промежутков [![]() ),
[
),
[![]() ),
…..[
),
…..[![]() )
т.е
)
т.е
![]()
![]() …..
…..
![]() .
.
