
- •Глава 1. Основные задачи математической статистики. Выборки и их характеристики.
- •§ 1. Предмет и задачи математической статистики.
- •§ 2. Генеральная и выборочная совокупность. Способы отбора.
- •§ 3. Статистическое распределение выборки.
- •§ 4. Полигон и гистограмма.
- •§ 5 Эмпирическая функция распределения.
- •§ 6. Числовые характеристики статистического распределения выборки.
- •§ 7. Числовые характеристики генеральной совокупности.
- •Глава 2.
- •§1 Понятие о статистических оценках параметров распределения.
- •§2. Точечные и интервальные оценки. Доверительный интервал. Точность оценки. Доверительная вероятность (надежность).
- •§3. Несмещенные, состоятельные и эффективные оценки.
- •§ 4. Точечная оценка генерального среднего по выборочной средней.
- •§ 5. Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии.
- •§6. Метод моментов для точечной оценки параметра распределения.
- •Глава 3.
- •§1. Статистическая гипотеза. Основные понятия.
- •§2. Ошибки первого и второго рода.
- •§ 3. Статистический критерий. Критическая область. Область принятия гипотезы. Критические точки.
- •§ 4. Уровень значимости и мощность критерия.
- •§ 5. Виды критических областей.
- •§6. Методика проверки гипотезы.
- •§ 7. Некоторые типичные задачи проверки параметрических гипотез.
- •7.1 Проверка гипотез о среднем значении.
- •7.2 Сравнение дисперсий 2-ух совокупностей.
- •§ 8. Непараметрические гипотезы. Критерии согласия Пирсона и Колмогорова.
- •8.1 Критерий Пирсона.
- •Глава 4.
- •§ 1. Основные понятия.
- •§ 2. Элементы теории корреляции. Анализ парных связей.
- •§ 3. Оценка показателя связи по выборочным данным. Корреляционное поле.
- •§ 4. Анализ коэффициента корреляции.
- •4.1 Точечная оценка коэффициента корреляции.
- •4.2 Интервальная оценка коэффициента корреляции и проверка значимости.
- •§ 5. Регрессионный анализ. Условные средние. Выборочные уравнения регрессии.
- •§ 6. Корреляционная таблица. Выборочные линии регрессии.
- •§ 7. Линейная регрессия. Выборочный коэффициент корреляции.
- •Глава 5. Основы дисперсионного анализа.
- •§ 1. Исходные понятия.
- •§ 2. Групповое и общее среднее. Групповая, внутригрупповая, межгрупповая и общая дисперсии.
- •§ 3. Однофакторный анализ при полностью случайном плане эксперимента.
- •§ 4. Двухфакторный анализ. (При полностью случайном плане экспериментов.)
§ 5. Регрессионный анализ. Условные средние. Выборочные уравнения регрессии.
При рассмотрении многомерных случайных величин рассматривались условные законы распределения и их числовые характеристики: математическое ожидание, дисперсия и различные моменты. Оценками этих величин служат их выборочные аналоги. Наиболее важными являются условные математические ожидания, вычисленные по выборке – условные средние.
Условное
среднее
![]() –
среднее арифметическое значений
случайной величины Y,
наблюдавшихся при фиксированном значении
случайной величины X=
x.
–
среднее арифметическое значений
случайной величины Y,
наблюдавшихся при фиксированном значении
случайной величины X=
x.
Условное
среднее
![]() –
среднее арифметическое значений
случайной величины X,
наблюдавшихся при фиксированном значении
случайной величины Y
=
y.
–
среднее арифметическое значений
случайной величины X,
наблюдавшихся при фиксированном значении
случайной величины Y
=
y.
Напомним определение уравнения регрессии:
![]()
условное
математическое ожидание
![]() является
функциейx.
является
функциейx.
Эта функция f (x)называется функцией регрессии Y на X, а ее график – линией регрессии.
Выборочный аналог
этого уравнения,![]() ,
называетсявыборочным
уравнением регрессии Y
на X,
функция
,
называетсявыборочным
уравнением регрессии Y
на X,
функция![]() –выборочной
функцией регрессии Y
на X,
ее график – выборочной
линией регрессии Y
на X.
–выборочной
функцией регрессии Y
на X,
ее график – выборочной
линией регрессии Y
на X.
Аналогично определяются выборочные характеристики и для регрессии X на Y.
§ 6. Корреляционная таблица. Выборочные линии регрессии.
Пусть
в результате эксперимента для системы
(Х,Y)
получена выборка значений
![]() .
.
Если значения х и y повторяются, то их группируют

Здесь
![]() и
и![]() – наблюдаемые значения X
и
Y,
а
– наблюдаемые значения X
и
Y,
а
![]() – частота появления пары значений
– частота появления пары значений![]() .
.
Чаще всего в этом случае данные организуют в виде корреляционной таблицы:
|
X Y |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
… |
… |
… |
…. |
…. |
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
Группируя данные
по значениям
![]() или
или
![]() :
:
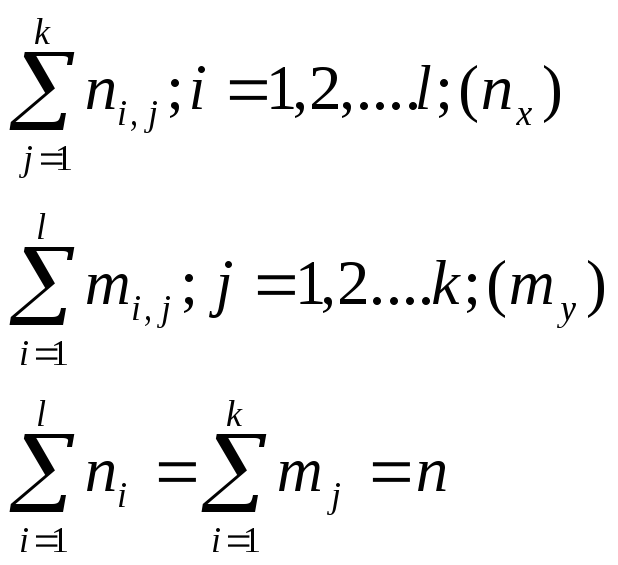
по
данным корреляционной таблицы можно
составить законы распределения
составляющих (последняя строка и
последний столбец таблицы) и их средние
по выборки
![]() и
и![]() .
.
![]() и
и
![]() .
.
Для
наглядности данные таблицы изображают
графически. Каждую пару (xi,yj)изображают
точкой в системе координат (ХОY).
Частоту
![]() ,
с которой данная пара встречается в
таблице, изображают соответствующим
числом близко расположенных точек либо
пишут число
,
с которой данная пара встречается в
таблице, изображают соответствующим
числом близко расположенных точек либо
пишут число![]() возле одной точки. Построенное таким
образом в системе координат изображение
корреляционной таблицы называютполем
корреляции.
Также возможно изображать
данные таблицы кругами, центр которых
находится в точке (xi,yj),
а диаметр (или площадь) пропорционален
возле одной точки. Построенное таким
образом в системе координат изображение
корреляционной таблицы называютполем
корреляции.
Также возможно изображать
данные таблицы кругами, центр которых
находится в точке (xi,yj),
а диаметр (или площадь) пропорционален
![]() .
.
Точка в системе
координат
(ХОY)
с координатами
![]() называетсяцентром
рассеивания.
называетсяцентром
рассеивания.
Можно
также составить условные законы
распределения, например Y
при Х=![]() или Х приY=
или Х приY=![]() .
.
|
|
|
|
…. |
|
|
|
|
|
….. |
|
Зная условные законы распределения, можно найти условные средние:
![]() и т.п.Построим в
системе координат (ХОY)
точки
и т.п.Построим в
системе координат (ХОY)
точки
![]() и соединим их
отрезками прямых. Полученную ломаную
называют
и соединим их
отрезками прямых. Полученную ломаную
называют
выборочной линией регрессии Y на X.
Если распределения случайных величин X и (или) Y заданы интервальным вариационным рядом, то удобно перейти к вспомогательным переменным, значения которых совпадают с серединами интервалов.
Кроме того, если варианты(значения вариационного ряда) являются равноотстоящими, т.е., образуют арифметическую прогрессию с разностью h, бывает удобно перейти к условным вариантам:
![]() ,
,
где C ложный нуль (новое начало отсчета),
h – шаг, т.е. разность между двумя соседними первоначальными вариантами (новая единица масштаба).
Если в качестве
ложного нуля взята какая-то из вариант
![]() , то условные варианты- целые числа, что
упрощает вычисления
, то условные варианты- целые числа, что
упрощает вычисления
![]()
