
КР Теория вероятностей
.docСургутский государственный университет
КОНТРОЛЬНЫЕ ЗАДАНИЯ
для бакалавров заочного отделения
Экономического факультета
по
теории вероятностей
кафедра высшей математики
преподаватель : к.ф.-м.н., доцент Аветисян Миша Грантович
Указания
-
При решении всех задач полагать число N равным последней цифре в зачете.
-
Для решения всех задач достаточно овладеть понятиями и формулами, которые можно найти в любом учебнике по теории вероятностей.
1.Имеются две урны, в первой из которых лежит 2 + N белых и 1 + N черных шаров, а во второй находятся 3 + N белых и 2 + N черных. Из первой урны один случайно выбранный шар переложили во вторую урну. После этого шары во второй урне перемешали и из нее стали по одному вынимать шары без возвращения.
Б1) Какова вероятность того, что первый вынутый из второй урны шар – черный?
Б2) Какова вероятность того, что и первый и второй вынутые из второй урны шары – черные?
Б3) Какова вероятность того, что переложенный шар – черный, если известно что и первый и второй шары, вынутые из второй урны – черные?
2.Дискретная случайная величина
![]() имеет таблицу распределения
имеет таблицу распределения
-
k
-2
-1
0
1
2
P(
 =k)
=k)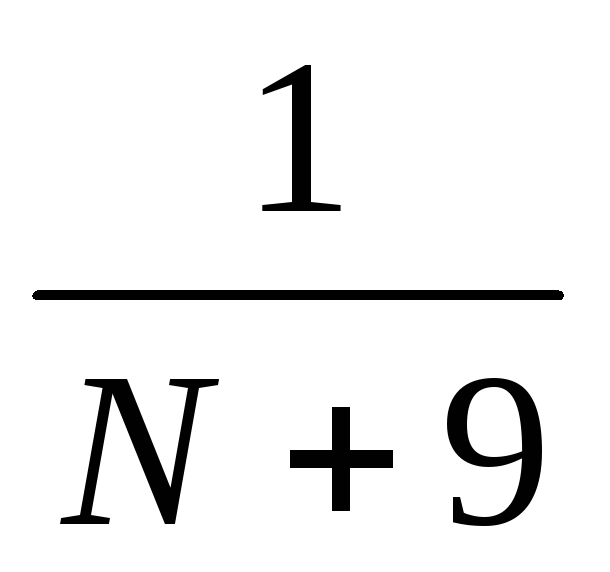
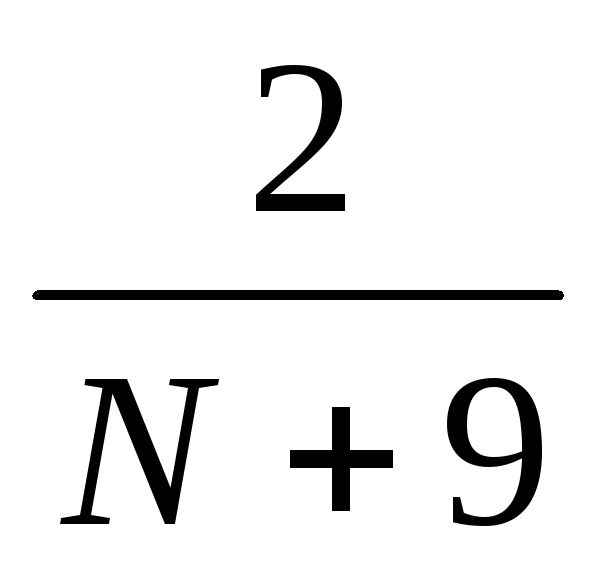
?
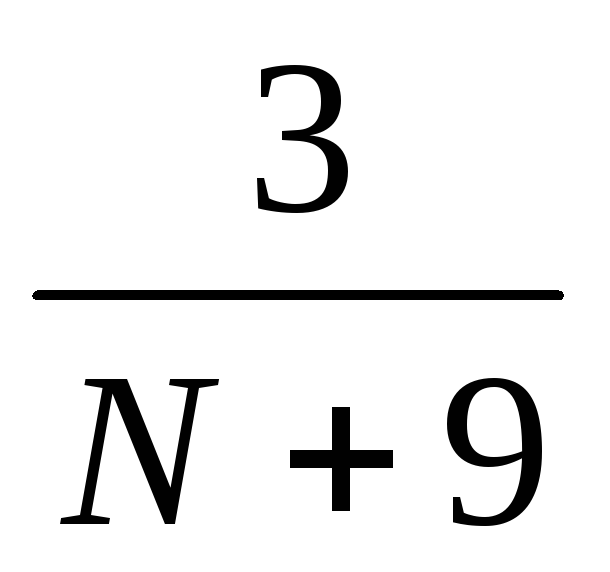
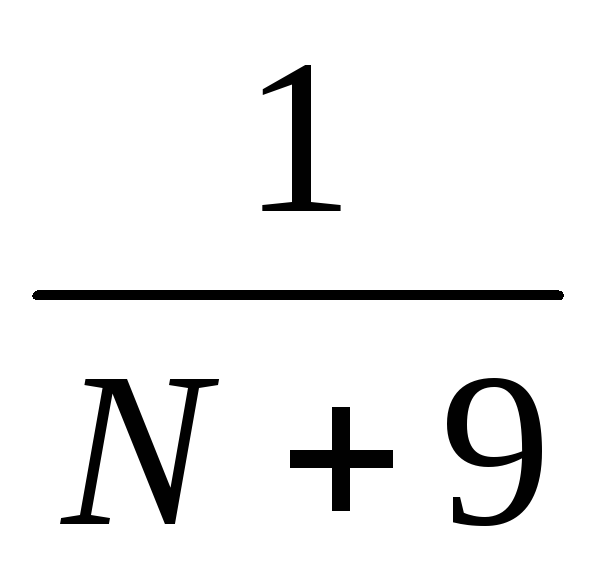
А1) Чему равна P(![]() = 0).
= 0).
А2) Найти P(![]() > 0).
> 0).
А3) Найти P(![]() <
2).
<
2).
А4) Найти P(![]() <
<![]()
![]() >
0).
>
0).
А5) Найти P(![]() >
>![]()
![]() <
2).
<
2).
А6) Найти M![]() и D
и D![]() .
.
А7) Пусть
![]() =(N+9)
=(N+9)![]() +
4.Найти M
+
4.Найти M![]() и D
и D![]() .
.
А8) Пусть
![]() =
=![]() .
Найти M
.
Найти M![]() и D
и D![]() .
.
3. Вариант 1. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
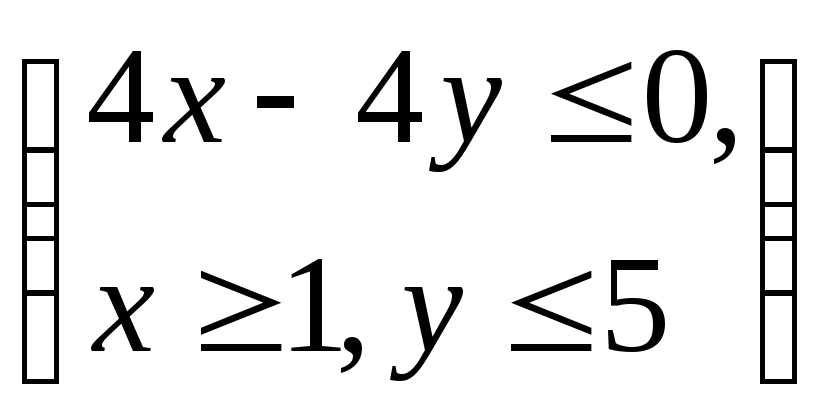
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 2. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
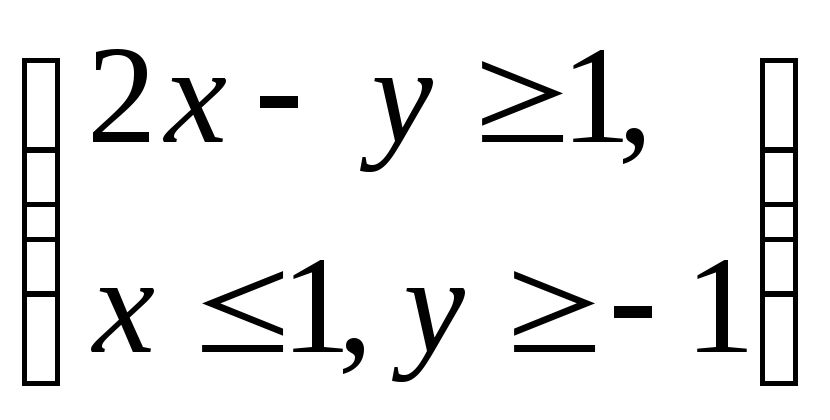
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 3. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
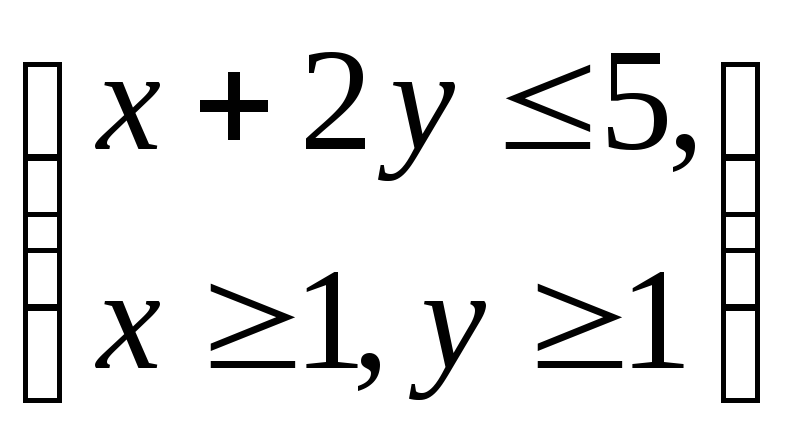
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 4. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
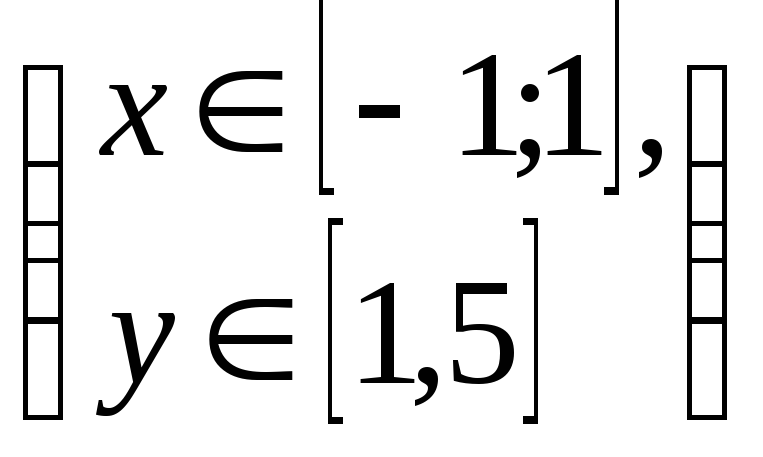
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 5. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
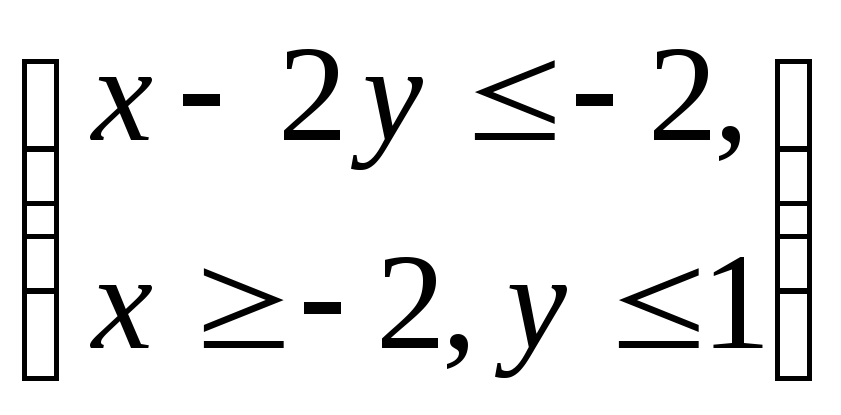
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 6. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
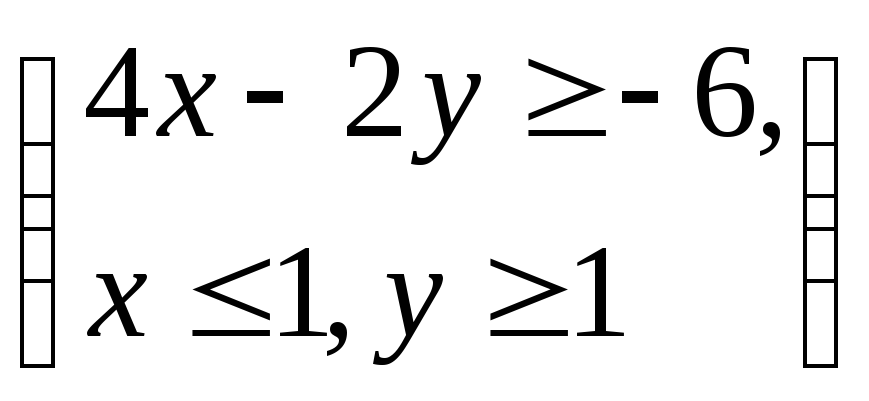
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 7. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
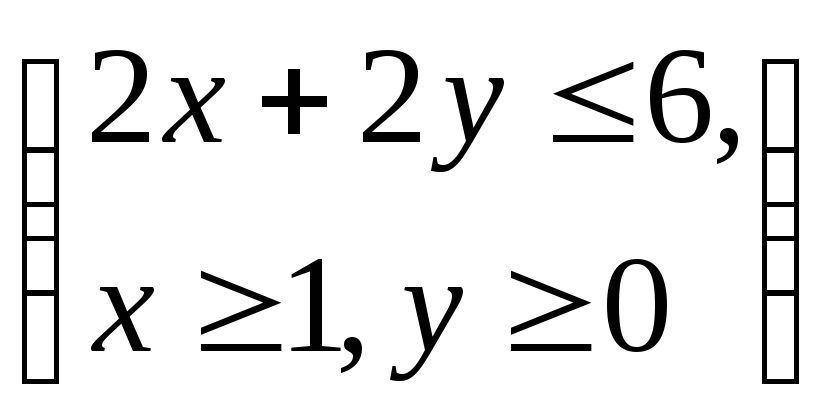
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 8. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
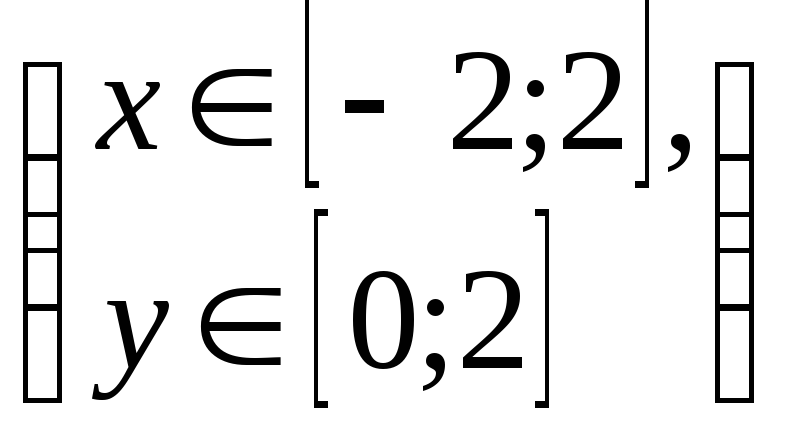
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 9. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
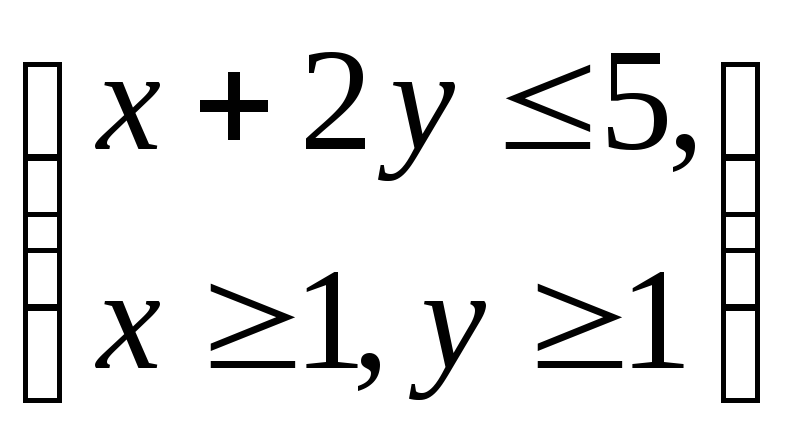
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
Вариант 10. Случайная величина
![]() имеет равномерное распределение в
области
имеет равномерное распределение в
области
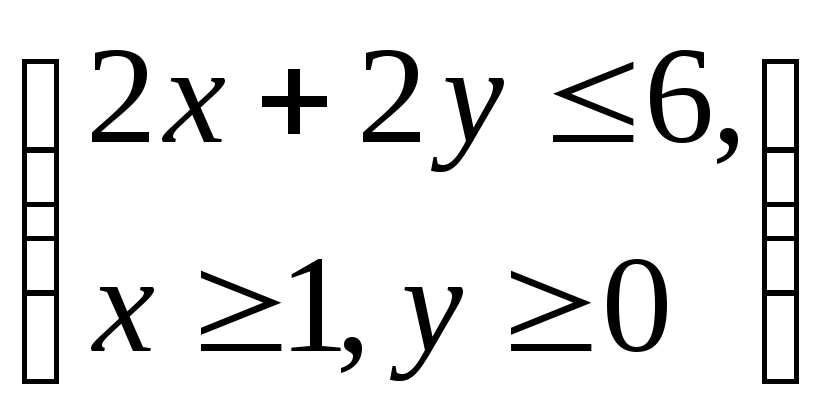
Найти
![]() плотность
распределения, совместную функцию
распределения.
плотность
распределения, совместную функцию
распределения.
4
Вариант№1
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№2
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№3
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№4
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№5
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№6
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№7
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№8
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№9
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
Вариант№10
Плотность двумерного нормального распределения имеет вид:
![]() e
x p
e
x p![]()
1.Вычислить вектор мат. Ожиданий и ковариационные характеристики данного случайного вектора.
