Контрольные вопросы

1. Какое движение тела называется поступательным?

2. Опишите виды поступательного движения.

3. Определите кинетические параметры поступательного движения (a, ,S) и объясните их физический смысл.

4. Запишите основные уравнения кинематики поступательного движения.

5. Как найти скорость и ускорение поступательного движения, если задан закон движения?

6. Сформулируйте законы Ньютона, запишите их в векторной и в скалярной формах.

7. Объясните методику проверки второго закона Ньютона.

Лабораторная работа № 10

ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ КРУЧЕНИЯ МЕТОДОМ

КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы: изучение крутильных колебаний и определение постоянной кручения методом крутильных колебаний.

Теоретическая часть

Всякое тело можно мысленно разбить на столь большое число малых частей (материальных точек) так, что размеры их будут малы по сравнению с размерами всего тела. Следовательно, тело всегда можно рассматривать как систему изматериальных точек, причем масса теларавна сумме масс всех этих точек:, где– массаi-той материальной точки.

Рассмотрим движение твердого тела, закрепленного в одной неподвижной точке О, вокруг которой тело может свободно вращаться. Точка О называется центром вращения твердого тела. Совместим с этой точкой начало неподвижной системы координат. Тогда положение в пространстве i-той точки тела полностью определяется радиус-век-тором , проведенным из точкиО в эту точку.

Сумма произведений масс всех материальных точек тела на квадраты их расстояний до оси вращения называется моментом инерции тела относительно этой оси. Момент инерции тела относительно оси О равен:

, (10.1)

где – расстояние от i-той материальной точки до оси вращения. При вычислении момента инерции, тело разбивают на бесконечно большое число бесконечно малых элементов с массами . Поэтому в формуле (10.1) суммузаменяют интегралом по объему этого тела:

, (10.2)

г

Рис. 10.1.

де– расстояние от элементадо осиО_z. По мере удаления тела от оси вращения, проходящей через центр инерции (центр масс), возрастает момент инерции тела. Это доказывает теорема Штейнера: момент инерции J_z' тела относительно любой оси ОО₁ равен сумме момента инерции J_z тела относительно оси О^'O₁^', проведенной через центр инерции С тела параллельно ОО₁, и произведения массы тела на квадрат расстоянияа между этими осями (рис. 10.1):

, (10.3)

В таблице 10.1 приведены формулы для вычисления моментов инерции однородных тел простейшей формы.

Таблица 10.1

Тело	Положение оси Оz	Момент инерции
Полый тонкостенный цилиндр радиуса R, имеющий массу	Ось симметрии
Сплошной цилиндр (или диск) радиуса R, имеющий массу m	Ось симметрии
Прямой тонкий стержень, имеющий длину и массу	Ось перпендикулярна к стержню и проходит через его середину
Тот же стержень	Ось перпендикулярна к стержню и проходит через его конец
Шар радиуса R, имеющий массу	Ось проходит через центр шара
Тот же шар	Ось проходит на расстоянии а от центра шара

Вычислить момент инерции тела относительно оси можно используя момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О. В случае непрерывного распределения масс эта сумма сводится к интегралу . Но момент инерциине следует смешивать с моментом инерцииотносительно оси. В случае моментамассыумножаются на квадраты расстояний до этой оси, а в случае момента– до неподвижной точки.

Рассмотрим сначала одну материальную точку с массой и с координатамих, y, z относительно прямоугольной системы координат (рис.10.2). Квадраты расстояний ее до координатных осей X, Y, Z равны соответственно, а моменты инерции относительно тех же осей:Сложив эти три равенства, получим:Но, гдеR –- расстояние точки от начала координатО. Поэтому:

, (10.4)

где .

Э

Рис. 10.2.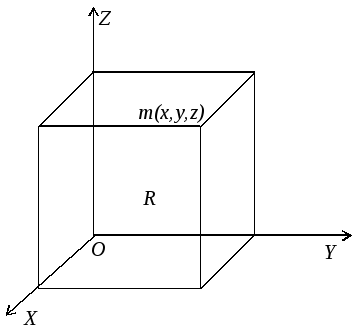

то соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точкеО, равна удвоенному моменту инерции того же тела относительно этой точки.

Если повернуть координатные оси Х, Y, Z относительно тела, оставляя углы между ними прямыми, то моменты инерции J_x, J_y, J_z изменятся. Однако их сумма останется той же самой, так как равна 2, а величина  не зависит от ориентации координатных осей. Таким образом, сумма моментов инерции J_x, J_y, J_z относительно любых трех взаимно перпендикулярных осей, проходящих через одну точку, зависит только от положения этой точки и не меняется с изменением ориентации осей.

Используя соотношение (10.4), рассмотрим случай плоского распределения массы. Допустим, имеется пластинка произвольной формы с произвольным распределением вещества по ее объему. Если пластинка очень тонкая, то можно считать, что вещество распределено бесконечно тонким слоем по плоскости. Примем эту плоскость за координатную плоскостьXY. Тогда z – координаты всех материальных точек будут равны нулю, а потому момент инерции  пластинки относительно начала координат О – , т.е. будет равен моменту инерции пластинки относительно осиZ. Таким образом, в случае плоского распределения масс , т. е.:

. (10.5)

Приведем пример вычисления момента инерции тонкого однородного стержня относительно перпендикулярной оси.

Пусть ось проходит через конец стержняА (рис.10.3). Для момента инерции можно написать , где – длина стержня. Центр стержня С является его центром масс. По теореме Гюгенса-Штейнера . Величину J_C можно представить как сумму моментов инерции двух стержней СА и СВ, длина каждого из которых равна , масса , а следовательно, момент инерции равен . Таким образом, . Подставляя эти выражения в предыдущую формулу, получим: , откуда. В результате находим:

, (10.6)

. (10.7)

Аналогично можно вычислить момент инерции однородной прямоугольной пластинки и прямоугольного параллелепипеда. Пусть координатные оси X и Y проходят через центр пластинки С и параллельны ее сторонам (рис.10.4). Допустим, что все вещество пластинки смещено параллельно от оси Х к оси Y. При таком смещении все расстояния материальных точек до оси Х не изменятся. Не изменится и момент инерции J_х относительно оси Х. Но в результате смещения пластинка перейдет в бесконечно тонкий стержень длины , к которому применима формула (10.7). В результате получим:

. (10.8)

Момент инерции I_Z пластинки относительно оси Z, перпендикулярной к ее плоскости, найдется по формуле (10.5), которая дает:

. (10.9)

Рис.10.4

Формула (10.9) годится также для вычисления моментов инерции прямоугольного параллелепипеда (куба) относительно его геометрических осей. В этом можно легко убедиться, если мысленно сжать параллелепипед (куб) вдоль одной из геометрических осей в прямоугольную пластинку – при таком сжатии момент инерции относительно этой оси не изменяется. Формула (10.9) дает момент инерции прямоугольного параллелепипеда относительно той его геометрической оси, которая проходит через центр основания с длинами сторон а и b. На рис.10.4 эта ось перпендикулярна к плоскости рисунка. Для куба (а = b) формула (10.9) запишется в виде:

. (10.10)

Наиболее простым методом является определение момента инерции тела при помощи крутильного маятника. Крутильный маятник представляет собой симметричное тело (рамка, диск и т.д.), подвешенное на тонкой нити. Если повернуть его в горизонтальной плоскости на угол , то в закручивающейся нити подвеса возникнут силы, возвращающие тело в начальное положение. При небольших углах закручивания момент этих сил пропорционален углу (упругая деформация) , и уравнение движения имеет вид:

, (10.11)

где J – момент инерции тела, D – постоянная момента упругих сил (постоянная кручения),  – угол закручивания (угловое перемещение). Так как уравнение (10.11) по форме не отличается от уравнения движения гармонического осциллятора: , то будут совпадать и решения обоих уравнений. Следовательно, крутильный маятник совершает гармонические колебания с частотой:, и периодом:

. (10.12)

Для определения момента инерции тела методом крутильных колебаний надо это тело закрепить на крутильном маятнике и измерить период колебаний Т. Но при этом должны быть известны постоянная кручения и момент инерции свободной рамки. Вычислить постоянную кручения D можно следующим образом: 1) подобрать некоторое тело правильной геометрической формы (например, куб); 2) вычислить его момент инерции J_Э по формуле (10.10); 3) закрепить это тело в рамке крутильного маятника; 4) измерить период колебаний этого тела Т_Э.

Момент инерции маятника равен сумме момента инерции J₀ свободной рамки и момента инерции J_Э эталонного тела (куба): . Поэтому период колебаний маятника (рамки с закрепленным в ней кубом):

. (10.13)

Отсюда находим выражение для постоянной момента упругих сил (постоянной кручения):

. (10.14)

Если колеблется свободная рамка без тела, то ее период колебаний равен:

. (10.15)

Момент инерции свободной рамки можно выразить из формул (10.13) и (10.15), получим:

. (10.16)