Измерения и обработка результатов

1. Зарисовать таблицу.

№	, мм	, мм	, мм	, мм
1. 2. 3. 4. 5.
	=		=

Измерить по пять раз (в различных местах) микрометром диаметр и штангенциркулем высоту цилиндра. Результаты измерения занести в таблицу.

2. Найти средние значения результатов прямых измерений величин и, вычислить и . Результаты занести в таблицу.

3. Оценить случайные, систематические и полные погрешности результатов прямых измерений величин. Записать окончательные результаты прямых измерений.

4. Вычислить объем цилиндра, т.е. найти результат косвенного измерения величины , оценить абсолютную и относительную погрешности косвенного измерения величины и записать для нее окончательный результат.

Контрольные вопросы

1. Как производятся измерения штангенциркулем и микрометром?

2. Как находятся результаты прямых и косвенных измерений величин?

3. Как производится оценка погрешностей прямых и косвенных измерений?

4. Что такое доверительная вероятность и доверительный интервал?

5. Как записывается окончательный результат?

6. Получите формулу для вычисления абсолютной и относительной погрешностей объема цилиндра.

Лабораторная работа № 2 изучение законов сохранения импульса и энергии при столкновении шаров

Цель работы: исследование столкновений тел; проверка закона сохранения импульса (количества движения); определение времени соударения; нахождение коэффициентов восстановления скорости и потери механической энергии.

Теоретическая часть

При решении многих задач в механике закон сохранения энергии применяют совместно с законом сохранения импульса. Классическим примером применения обоих законов сохранения является задача о столкновении тел. Взаимодействие между телами, в этом случае, происходит в течении короткого промежутка времени. При таких кратковременных взаимодействиях возникающие внутренние силы настолько велики, что значительно превосходят внешние, и поэтому соударяющиеся тела можно считать замкнутой механической системой.

Сталкивающимися телами могут быть и бильярдные шары, и молекулы, и элементарные частицы, т.к. законы сохранения импульса и энергии справедливы не только в классической, но и в квантовой физике. Столкновениями объясняется механизм многих явлений. Такие процессы, как теплопроводность газов, диффузия, способность газов оказывать сопротивление движущимся в них телам, определяются столкновениями молекул друг с другом. Химические реакции в веществах, находящихся в газообразном состоянии, происходят также вследствие столкновения молекул. Рассеянием электронов на неоднородностях кристаллической решетки, объясняется свойство электрической проводимости тел.

Различаются два вида столкновений. Упругими называются столкновения, в результате которых суммарная кинетическая энергия тел не изменяется. Если этого не происходит, то столкновения называют неупругими.

Рассмотрим процесс столкновения двух стальных шаров, подвешенных на нитях одинаковой длины .

m₂ m₁

Рис. 2.1.

Если отклонить шар массой m₁ на угол ₀ и отпустить, то он, ударившись упруго о неподвижный шар массой m₂, передаст ему часть своей энергии и импульса (рис.2.1).

После удара шары отклоняются на углы ₁ и ₂, а их центры масс при этом поднимутся на высоты h₁ и h₂ по отношению к линии удара, т.е. кинетические энергии шаров, приобретенные ими после удара, перейдут в потенциальные. Запишем закон сохранения импульса для данной системы, беря проекции векторов на ось Х (при условии, что m_1> m₂):

_(2.1)

где v₁ – скорость первого шара до удара; u₁ и u₂ – скорости первого и второго шаров после удара.

Закон сохранения механической энергии для системы сталкивающихся шаров можем представить в виде:

_(2.2)

При малых углах отклонения маятников ():

sin (рад). (2.3)

Тогда из (2.2) и (2.3) следует, что:

, (2.4)

. (2.5)

Из уравнения (2.1) можно выразить u₂:

. (2.6)

Скорость v₁ можно определить подобным (2.4), (2.5) образом:

. (2.7)

Подставив (2.4), (2.5), (2.7) в уравнение (6), получаем:

. (2.8)

В этом выражении ₀, ₁ и ₂ могут записываться как в радианах, так и в градусах.

Закон сохранения импульса (2.1) определяет линейную зависимость между скоростями v₁, u₁ и u₂, а так как эти скорости линейно связаны с соответствующими углами (₀, ₁, ₂) – то и линейную зависимость между углами ₀, ₁, ₂. Поэтому, если график зависимости ₂ от (₀ - ₁), полученный экспериментально, окажется прямой (с учетом погрешности), то это будет свидетельствовать о выполнении закона сохранения импульса.

Реальные материалы (металлы, полимеры и т.п.) конечно не являются абсолютно упругими телами. Поэтому при столкновении двух стальных шаров в экспериментальных исследованиях закон сохранения механической энергии не выполняется, а именно: часть механической энергии переходит во внутреннюю энергию деформируемых тел, что вызывает их нагревание.

В этом случае закон сохранения энергии будет иметь вид:

, (2.9)

где:– кинетическая энергия первого шара до и после удара,– кинетическая энергия второго шара,Q – часть механической энергии, которая переходит во внутреннюю энергию этих шаров после столкновения.

Преобразуем уравнение (2.9):

. (2.10)

Используя (2.1) получаем, что:

. (2.11)

Обозначим величину черезК, тогда –коэффициент восстановления скорости, который характеризует меру упругости тел при взаимодействии. При абсолютно упругом столкновении Q=0 и, следовательно, К=1.

Из уравнений (2.4) – (2.6) и (2.11) получаем:

, (2.12)

т.е. если закон сохранения импульса выполняется и в том случае, когда имеются потери механической энергии (неупругие столкновения), то в пределах погрешности измерений зависимость (₂-₁) от ₀ должна быть линейной, а тангенс угла наклона определять значение К.

Величина называется коэффициентом потери механической энергии при столкновении шаров.

Произведя преобразование выражения (2.11) с учетом (2.5) и (2.6), получаем:

. (2.13)

На основании экспериментальных данных в силу линейной зависимости ₂ от ₀ (2.13) можно определить коэффициент потери механической энергии , определяя тангенс угла полученного графика.

Сила взаимодействия при столкновении, согласно второму закону Ньютона, определяется изменением импульса каждого шара и временем соударения : где – сила, действующая со стороны второго шара на первый; – сила, действующая со стороны первого шара на второй;– изменение импульса первого шара;– изменение импульса второго шара. Учитывая (2.4) – (2.6), получаем (для проекции векторов на ось Х):

, .

Средняя сила взаимодействия при столкновении шаров определяется при этом как:

. (2.14)

Рассмотрим частный случай неупругого столкновения, а именно: полностью неупругое столкновение, после которого скорости обоих соударяющихся тел оказываются одинаковыми. Это возможно, если при деформации тел возникают силы, зависящие не от величины деформации, а от скорости изменения деформации. Таким свойством обладают, например, пластилиновые тела.

Рис. 2.2

Показать случай полностью неупругого столкновения можно при помощи шаров из пластилина, подвешенных на нитях длиной (рис.2.2).

Если отклонить шар массой m₁ на угол ₀ и отпустить, то после столкновения оба шара «слипаются» и дальше движутся вместе как одно целое с одинаковой скоростью. Из аддитивности масс следует, что масса тела, образовавшегося в результате «слипания» шаров, равна сумме их масс. Тогда закон сохранения импульса можно записать в виде:

, (2.15)

где v₁ – скорость первого шара до соударения; u₁₂ – скорость первого и второго шаров после соударения.

При малых углах отклонения первого шара аналогично (2.4) и (2.7) скорости v₁ и u₁₂ определяются следующим образом:

, .

Тогда (2.15) можно записать в виде:

. (2.16)

В этом выражении ₀ и  могут быть представлены, как в радианах, так и в градусах. Таким образом, если график зависимости  от ₀ в пределах погрешности измерений будет являться прямой, то это будет свидетельствовать о выполнении закона сохранения импульса и при полностью неупругом столкновении тел.

В случае подобных столкновений, как видно из (2.11) при u₁=u₂=u₁₂, величина потерь механической энергии будет максимальной (К=0): , а коэффициент потери механической энергии зависит только от соотношения масс сталкивающихся тел:

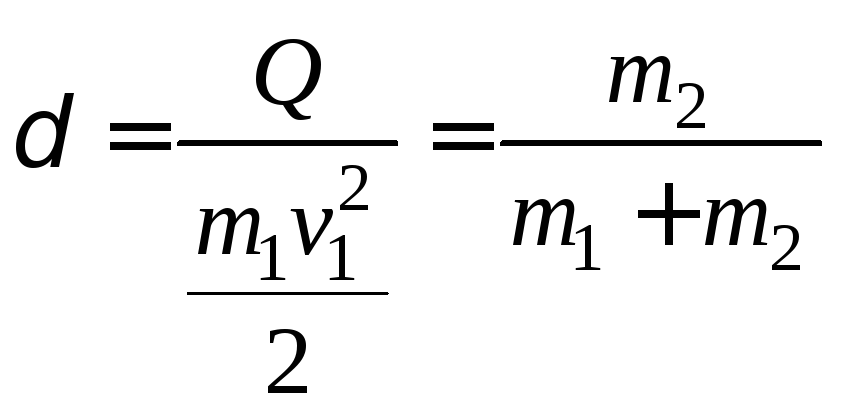. (2.17)