Контрольные вопросы

1. Дайте определение момента инерции.

2. Поясните физический смысл понятия момента инерции.

3. Какие оси называют главными осями инерции?

4. Как вычислить момент инерции тела относительно оси вращения параллельной одной из главных осей?

5. Покажите, что момент инерции однородного куба относительно оси, проходящей через его центр, .

6. Выведите формулы (10.6), (10.7), (10.9) и (10.12).

7. Что такое крутильный маятник?

8. Сформулируйте теорему Штейнера.

9. Определите физический смысл постоянной кручения D.

10. Объясните методику определения момента инерции свободной рамки маятника.

Лабораторная работа № 11 определение скорости пули с помощью крутильного баллистического маятника

Цель работы: изучение закона сохранения момента импульса и основного уравнения динамики вращательного движения; измерение скорости пули методом крутильного баллистического маятника.

Теоретическая часть

Метод крутильного баллистического маятника, используемый в данной работе для определения скорости пули, основан на применении закона сохранения момента импульса и основного уравнения динамики вращательного движения твердого тела. Моментом импульса материальной точки Аотносительно неподвижной точкиОназывается физическая величина, определяемая векторным произведением (рис. 11.1):

Рис. 11.1

, (11.1)

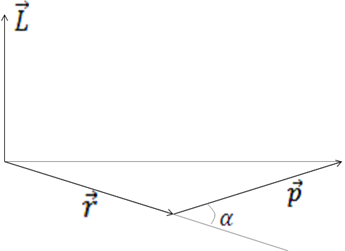
где: − радиус-вектор, проведенный из точкиО в точку А, − импульс материальной точкиА. Модуль вектора момента импульса:

, (11.2)

где: α – угол между векторами.

При вращении твердого тела вокруг неподвижной оси Z каждая его частица массой m_i движется по окружности постоянного радиуса r_i с некоторой скоростью υ_i. Момент импульса отдельной частицы тела равен:

(11.3)

Момент импульса твердого тела относительно заданной оси есть сумма моментов импульса отдельных частиц тела:

(11.4)

Т.к. , то следует, что:

(11.5)

Таким образом, момент импульса твердого тела относительно оси Z равен произведению момента инерции тела относительно той же оси на угловую скорость вращения.

Если продифференцировать по времени это выражение, то получаем уравнение:

(11.6)

где: ε – угловое ускорение тела, – момент сил, действующих на тело относительно оси Z. Данное уравнение называется основным уравнением динамики вращательного движения и в векторном виде может быть представлено следующим образом:

(11.7)

В замкнутой системе момент внешних сил равен нулю и, следовательно, , поэтому: , откуда

. (11.8)

Это выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется со временем.

Примером применения закона сохранения момента импульса и уравнения динамики вращательного движения является удар (соударение) тел, в результате которого одно из них начинает вращаться.

Удар – это столкновение двух и более тел, при котором взаимодействие длится очень короткое время. Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При ударе в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.

Рис.11.2.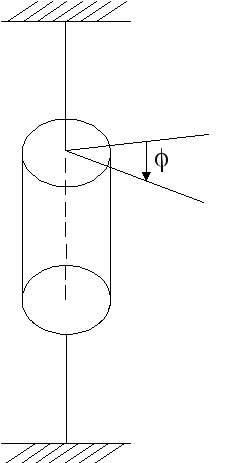

Соударение пули с баллистическим крутильным маятником является примером такого взаимодействия. Крутильный маятник представляет собой симметричное тело, подвешенное на тонкой нити (рис.11.2). Если повернуть его в горизонтальной плоскости на уголφ, то в закручивающейся нити подвеса возникают силы, возвращающие тело в начальное положение. При небольших углах закручивания момент этих сил пропорционален величине угла:

. (11.9)

где: D – постоянная упругих сил (постоянная кручения).

Когда горизонтально летящая пуля попадает в маятник и застревает в нем – происходит неупругий удар. После удара маятник начинает совершать крутильные колебания относительно тонкой нити. Угол поворота системы определяется уравнением, которое следует из основного закона динамики вращательного движения:

. (11.10)

где: J – момент инерции колебательной системы.

Решением этого уравнения является:

, (11.11)

где: φ₀ – максимальный угол отклонения маятника, ω – частота колебаний маятника. Согласно закону сохранения момента импульса начальные условия для данной системы имеют вид:

(11.12)

где: m –масса «пули», υ – ее скорость, ℓ – расстояние от оси вращения маятника до точки попадания «пули».

Можно определить, что:

(11.13)

где: и период колебаний. Из (11.12) и (11.13) следует:

. (11.14)

Момент инерции для данной колебательной системы можно рассчитать следующим образом:

(11.15)

где: m₀ – масса груза, ℓ₁ = 0,0525 м – расстояние от оси вращения до центров масс грузов, – момент инерции рамки.

Период колебаний свободной рамки:

(11.16)

Отсюда следует, что:

. (11.17)

Из этого соотношения можно определить момент инерции колебательной системы:

. (11.18)

Скорость «пули» можно определить из (11.14), используя (11.18):

. (11.19)