Микропроцессоры Токхайм / 2.3. ВОСЬМЕРИЧНЫЕ ЧИСЛА

2.3. ВОСЬМЕРИЧНЫЕ ЧИСЛА

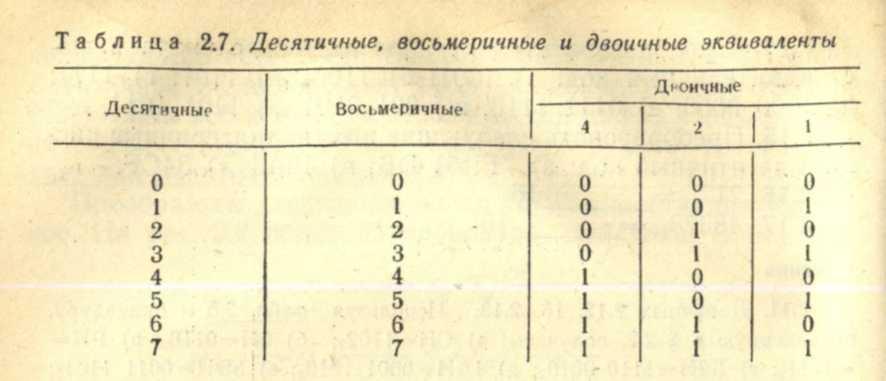
Восьмеричная запись, как и шестнадцатеричная, исполь­зуется для представления двоичных чисел. Восьмеричная система содержит 8 цифр от 0 до 7 и является соответствен­но системой с основанием 8. В табл. 2.7 представлено не­сколько десятичных, восьмеричных и двоичных чисел.

Преобразуем двоичное число 11111000100 в его восьме­ричный эквивалент. Процедура действий в этом случае сле­дующая. Начиная с МБ двоичного числа, делим его на группы из 3 бит. Затем, используя табл. 2.7, преобразуем каждую триаду (группу из 3 бит) в эквивалентную восьме­ричную цифру. Таким образом, мы заменим двоичное число 11111000100 его восьмеричным эквивалентом 37048:

Двоичное число 011 111 000 100

Восьмеричное число 3 7 0 4

Преобразуем теперь восьмеричное число 6521 в его дво­ичный эквивалент. Каждая восьмеричная цифра заменяет­ся двоичной триадой и получится, что 65218= 110101010001 2".

Запишем восьмеричное число 2357 в десятичной форме. Классическая процедура выполняется согласно табл. 2.8. Здесь 512, 64, 8 и 1 есть веса четырех первых восьмеричных позиций. Заметим, что в этом примере содержится 7 еди­ниц, 5 восьмерок, 4 числа 64 и два числа 521. Мы их скла­дываем и получаем результат: 1024+192+40+7= 1263 10.

Наконец, преобразуем десятичное число 3336 в его вось­меричный эквивалент. Процедура показана на рис. 2.3. В первую очередь 3336 разделено на 8, что дает частное 417 и остаток 0 10, причем 0 10=08, восьмеричный 0 становится значением MP восьмеричного числа. Первое частное (417) становится делимым и снова делится на 8 (вторая строка), что дает частное 52 и остаток 110=18, который становится второй цифрой восьмеричного числа. В третьей строке ча­стное (52) становится делимым и деление его на 8 дает частное 6 и остаток 4 10=48. В четвертой строке последнее частное 6 разделено на 8 с частным 0 и остатком 6 10=68.

Теперь счет закончен последним частным 0. Цифра 68 ста­новится значением CP восьмеричного числа, и мы можем видеть на рис. 2.3, что 3336ю=64108.

Большинство микропроцессоров и микро-ЭВМ обраба­тывают группы из 4, 8 или 16 бит. Отсюда следует, что обычно чаще используется шестнадцатеричная запись, чем восьмеричная. Однако восьмеричная запись более удо­бна, когда группы бит делятся на 3 (например, группы из 12 бит).

Упражнения

2.18. Для представления двоичных чисел текст докумен­тации 8-разрядного микропроцессора использует _

(шестнадцатеричную, восьмеричную) систему.

2.19. Другим названием восьмеричной системы является

2.20. Записать следующие восьмеричные числа в двоич­ном коде: а) 3; б) 7; в) 0; г) 7642; д) 1036; е) 2105.

2.21. Записать следующие двоичные числа в восьмерич­ном коде: а) 101; б) 110; в) 010; г) 111000101010; д) 1011000111; е) 100110100101.

2.22. 67248=_____10.

2.23. 2648 10=____8.

Решения

2.18. Шестнадцатеричную, при которой удобно представить двоич­ное число двумя 4-разрядными группами. 2.19. Система с основанием 8. 2.20. а) 38=0112; б) 78=1112; в) 08 = 0002; г) 76428= 1111101000102;

д) 10368= 10000111102; е) 21058= 100010001012. 2.21. а) 1012=58; б) 1102=68; в) 0102=28; г) 1110001010102 = 70528; д) 10110001112= 13078;

е) 1001101001012 = 46458. 2.22. Согласно процедуре табл. 2.8: 67248= = (512Х6) + (64х7) + (8х2) + (1Х4)=3540 10. 2.23. Согласно процедуре рис. 2.3:

2648 10 : 8 = 331, остаток 0 (MP); 331 : 8= 41, остаток 3; 41 : 8= 5, остаток 1; 5 : 8= 0, остаток 5 (CP); 2648 10=51308.