
Векторы s1 , s2 , M1M2 некомпланарные, (см. задачу 143), в
частности s1 ||/ s2 . Здесь
M1 (x1 , y1 , z1 ) L1 , M2 (x2 , y2 , z2 ) L2 .
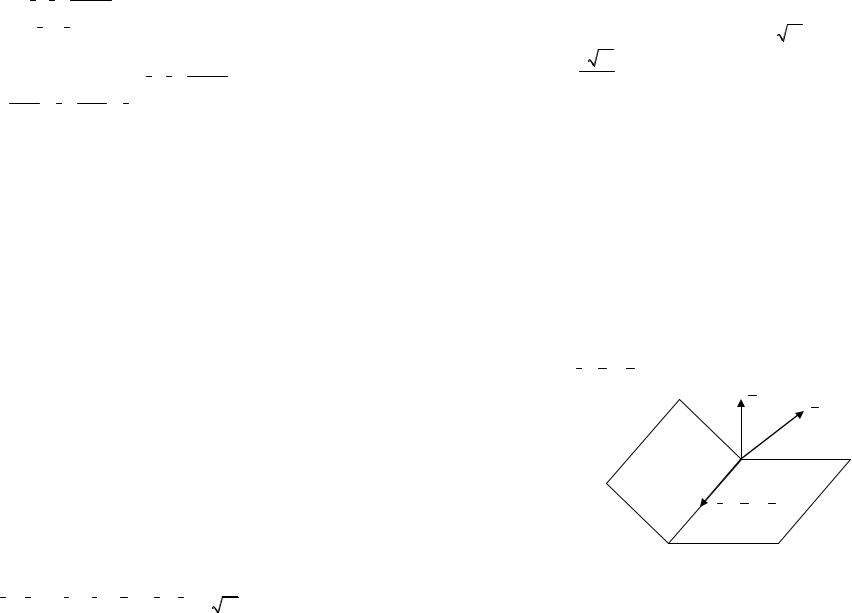
Отложим все три вектора s1 , s2 , M1M2 от одной точки M1 . Здесь M1A =s1, M1B =s2 . Из рисунка 49 ясно, что прямая L2 параллельна грани M1AB , т.к. прямая L2 по построению параллельна ребру M1B треугольной пирамиды M1M2 AB (если прямая параллельна какой-нибудь прямой,
лежащей в плоскости, то она параллельна этой плоскости.). Следовательно, расстояние между скрещивающимися прямыми d(L1 , L2 ) равно расстоянию от прямой L2 до грани
M1AB , а это расстояние, в свою очередь, равно высоте
H = M2 O пирамиды |
M1M2 AB, опущенной из вершины |
|||||||||||||||||||||||||||||||||||||
M2 на грань M1AB : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
1 | |
|
1 |
|
2 |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3VM M |
|
s |
s |
M M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
AB |
|
2 |
|
| s1 s2 |
M M |
|
|
| |
|
|
|
||||||||||||||||||||||||||
H = |
= |
|
6 |
|
|
|
|
|
|
1 |
|
= |
2 |
. |
|
|
||||||||||||||||||||||
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
SM AB |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| s1 |
×s2 | |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
2 | s1 ×s2 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. |
Установить, |
что прямые |
|
L : |
x −1 |
|
= |
y +1 |
= |
z |
и |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
−1 |
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
L2 : x = y = z +1 скрещивающиеся, и найти расстояние между ними.
Решение. M1 (1; −1; 0) , M2 (0; 0; −1) , |
M1M2 |
= (−1; 1; −1) , |
||||||||||
|
|
1 = (2; −1; 0) , |
|
2 = (1; 1; 1) , |
|
1 |
|
2 |
|
|
= −4 , |
т.е. данные |
|
s |
s |
s |
s |
M1M2 |
|
||||||
прямые скрещивающиеся. Находим расстояние между ни-
ми: s1 ×s2 = −i − 2 j + 3k , | s1 ×s2 | = 14 , 121
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
d = |
s |
1 s |
2 M1M2 | |
= |
4 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
| s1 ×s2 | |
14 |
|||||||||
|
|
|
|
|
|
||||||||
Ответ: 2 14 . 7
Задача 148. Найти каноническое уравнение прямой, заданной пересечением двух плоскостей.
Решение. Пусть прямая задана пересечением двух плоскостей L = α ∩β:
|
|
L : |
|
A x +B y +C z +D = 0 |
. |
(1) |
|||||
|
|
|
1 |
1 |
1 |
1 |
|||||
|
|
|
A2x +B2 y +C2z +D2 = 0 |
|
|
||||||
Пусть |
|
1 = (A1 , B1 , C1 ) и |
|
|
2 |
= (A2 , B2 , C2 ) |
|
– нормальные |
|||
n |
n |
|
|||||||||
векторы данных плоскостей. Так как прямая, перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, то оба нормальных вектора перпендикулярны прямой пересечения L, и их векторное произведение будет вектором, коллинеарным этой прямой. Поэтому, в качестве направляющего вектора прямой можно взять
вектор s = n1 ×n2 .
n2
n1
α
β
L |
s = n1 ×n2 |
|
Рис. 50.
Таким образом, вычисляя векторное произведение нормальных векторов плоскости (неважно в каком порядке),
122

мы находим направляющий вектор прямой L: s = n1 ×n2 = (m, n, p) .
Далее, найдем какое-нибудь решение (xo , yo , zo ) системы
(1). Т.к. любое решение системы (1) есть координаты точки, лежащей на обеих плоскостях, то тем самым мы находим точку на прямой L. Теперь осталось написать канонические уравнения прямой L:
|
x − xo |
|
= |
y − yo |
= |
z − zo |
. |
||
|
m |
|
|
n |
|
||||
|
|
|
|
|
p |
|
|
||
Пример. Найти канонические уравнения прямой |
|||||||||
|
L : |
|
|
x +2y −z +1 = 0 |
. |
||||
|
|
2x −y +2z −3 = 0 |
|||||||
|
|
|
|
|
|||||
Решение. Исключим из уравнения одно из переменных. Умножим, например, первое уравнение на 2 и сложим оба уравнения. Получаем 4x + 3y −1 = 0 . Положим в этом
уравнении y = 3. Получаем x = −2 . Подставляя найденные
значения х и у в первое уравнение, находим z = 5 .
Таким образом, точка с координатами (−2;3;5) лежит на данной прямой, т.е. xo = −2, yo = 3, zo = 5 . Найдем ее
направляющий вектор. Выписываем нормальные векторы данных плоскостей и вычисляем их векторное произведение:
|
n |
1 = (1, 2, −1) , |
|
|
n |
2 = (2, −1, 2) , |
s |
= |
n |
1 × |
n |
2 = (3; −4; −5) . |
Таким образом, |
|
= (3, − 4, −5) , т.е. m = 3, n = −4, p = −5 и, |
||||||||||
s |
||||||||||||
подставляя эти числа в канонические уравнения, получаем Ответ: x +3 2 = y−−43 = z−−55 .
Задача 149. Задать прямую пересечением двух плоскостей, зная ее каноническое уравнение.
123
Решение. Пусть дано каноническое уравнение прямой: x −mxo = y −nyo = z −pzo .
Перепишем этоуравнение в виде равносильнойему системы:
|
x −x |
o |
|
= |
y −y |
o |
|
||
|
|
|
|
|
|
||||
|
m |
|
n |
|
|
|
|||
|
|
|
|
|
|
|
. |
||
|
|
y −yo |
|
z −zo |
|||||
|
|
= |
|
||||||
|
|
n |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оба уравнения этой системы есть плоскости. Первая плос-
кость |
параллельна оси |
Oz |
(или содержит ее, если |
|||
xo = yo |
= 0 ), а вторая – |
оси Ох (или содержит ее, если |
||||
zo = yo |
= 0 ). Тем самым задача решена. |
|||||
Пример. Задать прямую |
x + 2 |
= |
y −3 |
= z −5 пересечением |
||
3 |
−4 |
|||||
двух плоскостей. |
|
−5 |
||||
|
|
|
|
|||
Решение. Записываем каноническое уравнение прямой в виде системы:
x +2 |
= |
y −3 |
|
|
|
−4(x + 2) = 3(y −3) |
|
|
4x +3y −1 = 0 |
|
||||||
|
3 |
−4 |
|
или |
, |
. |
||||||||||
|
||||||||||||||||
|
|
|
5(y |
−3) |
= 4(z −5) |
|
5y −4z +5 = 0 |
|||||||||
|
y −3 |
= |
z −5 |
|
|
|
|
|
|
|||||||
|
−4 |
−5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
4x |
+3y |
−1 |
= 0 |
. |
|
|
|
|
|
|
|||||
|
5y |
−4z |
+5 |
= 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 150. Найти уравнение плоскости, проходящей через данную прямую и параллельной другой прямой.
|
Решение. Пусть даны две прямые |
|
|
|
|
|||||||||
L : |
x − x1 |
= |
y − y1 |
= |
z −z1 |
и L |
2 |
: |
x − x2 |
= |
y − y2 |
= |
z −z2 |
|
|
|
|
|
|
|
|||||||||
1 |
|
m1 |
|
n1 |
|
p1 |
|
|
m2 |
|
n2 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
124 |
|
|
|
|
|
|
|

Так как одна прямая, например L1 , будет лежать в плоско-
сти, а вторая параллельна ей, то оба направляющих вектора данных прямых коллинеарны этой плоскости и, следовательно, перпендикулярны ее нормальному вектору. Поэтому нормальным вектором плоскости может служить век-
торное произведение направляющих векторов: n = s1 ×s2 ,
где s1 = (m1, n1;p1 ), s2 = (m2 , n2 ;p2 ) .
Если плоскость проводится через прямую L1 , то любая
ее точка принадлежит этой плоскости, в том числе и точка M1 (x1 , y1 ,z1 ) . Таким образом, у нас есть все для написания
общего уравнения плоскости (см. задачу 123): A (x −x1) +B(y − y1 ) +C(z −z1 ) = 0 ,
где (A, B, C) = n = s1 ×s2 – координаты нормального вектора.
Пример. Найти уравнение плоскости, проходящей через
прямую L : |
x −1 |
= |
y +1 |
= |
z |
параллельно прямой |
|
|
|
||||
1 |
2 |
|
−1 0 |
|||
|
|
|||||
L2 : x = y = z +1.
Решение. Находим нормальный вектор плоскости:
i j k
s1 ×s2 = 2 −1 0 = −i −2j +3k . 1 1 1
В качестве нормального вектора плоскости возьмем противоположный вектор: n = (A,B,C) = (1;2;−3) . В качестве точки, лежащей на плоскости возьмем точку M1 (1, −1,0) принадлежащую прямой L1 . Выписываем уравнение плоскости проходящей через точку M1 (1, −1,0) с нормальным вектором n = (A,B,C) = (1;2;−3) :
125
(x −1) + 2(y +1) −3(z −0) = 0 . Ответ: x + 2y −3z +1 = 0 .
Задача 151. Определить взаимное расположение прямой и плоскости.
Теорема. Пусть плоскость α задана общим уравнением
α: Ax+By+Cz+D=0,
апрямая L задана каноническим уравнением
L : x −mxo = y −nyo = z −pzo
или параметрическим уравнением
|
x = xo +mt |
|
L : |
|
y = yo +nt , t R , |
|
||
|
|
z = zo +pt |
|
|
|
в которых n = (A, B, C) – координаты нормального вектора плоскости α, Mo (xo , yo , zo ) – координаты произволь-
ной фиксированной точки прямой L, |
s |
= (m, n, p) |
– коор- |
||||||||||
динаты направляющего вектора прямой L. Тогда: |
|
||||||||||||
1) если |
|
|
|
|
|
= Am + Bn + Cp ≠ 0 , |
то прямая |
L пересекает |
|||||
n |
s |
||||||||||||
плоскость α в точке, координаты которой (x, y, z) |
можно |
||||||||||||
найти из системы уравнений |
|
|
|
|
|
||||||||
A (xo +mt) +B(yo +nt) +C(zo +pt) +D = 0 |
|
||||||||||||
|
|
|
|
|
|
|
x = xo +mt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
||
|
|
|
|
|
|
|
y = yo +nt |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
z = zo +pt; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) если |
|
|
|
= Am + Bn + Cp = 0 и |
Axo |
+ Byo |
+Czo |
+ D = 0 , |
|||||
n |
s |
||||||||||||
то прямая лежит на плоскости; |
|
|
|
|
|
||||||||
|
|
126 |
|
|
|
|
|
||||||

3) если |
n |
|
s |
= Am + Bn + Cp = 0 и Axo + Byo +Czo |
+ D ≠ 0 , |
то прямая параллельна плоскости. |
|
||||
Пример 1. Определить взаимное расположение |
прямой |
||||
L : x +4 = |
y −7 |
= z − |
2 |
и плоскости σ: 2x −2y + z +5 = 0 . |
−1 |
|
|||
|
3 |
|
|
Решение. Выписываем направляющий вектор прямой и нормальный вектор плоскости:
s = (1; −1; 3) , n = (2; − 2; 1) .
Вычисляем их скалярное произведение s n = 2 + 2 +3 = 7 ≠ 0 ,
следовательно, s n , и прямая пересекает плоскость.
Пример 2. Определить взаимное расположение прямой
L : x +4 = |
y −7 |
= |
z − |
2 |
и плоскости σ: 2x +2y −1 = 0 . |
−1 |
|
|
|||
|
3 |
|
|
||
Решение. Выписываем направляющий вектор прямой и нормальный вектор плоскости:
s = (1; −1; 3) , n = (2; 2; 0) .
Вычисляем их скалярное произведение s n = 2 −2 = 0 , следовательно, или прямая параллельная плоскости или прямая лежит на плоскости. Если прямая лежит на плоскости, то точка Mo (−4; 7; 2) L удовлетворяет уравнению
плоскости:
2 (−4) + 2 7 −1 = 5 ≠ 0 .
В данном случае координаты точки Mo (−4; 7; 2) L не
удовлетворяют уравнению плоскости, поэтому прямая L не лежит на плоскости. Остается последний случай – прямая параллельна плоскости.
Ответ: прямая и плоскость параллельны. 127
Замечание. Если прямая задана в виде пересечения двух плоскостей:
L : A1x +B1y +C1z +D1 = 0 ,A2x +B2 y +C2z +D2 = 0
то можно найти ее канонические уравнения и решать задачу как выше. Но можно поступить иначе.
Пусть плоскость α задана общим уравнением
α: Ax +By +Cz + D = 0 .
|
|
A x +B y +C z +D = 0 |
|||
|
|
1 |
1 |
1 |
1 |
Решим систему |
|
A2x +B2 y +C2z +D2 = 0 . |
|||
|
|
Ax +By +Cz +D = 0 |
|||
|
|
||||
Если система имеет единственное решение, то это решение дает координаты точки встречи прямой с плоскостью.
Если система не имеет решений, то прямая и плоскость параллельные.
Если система имеет бесконечно много решений, то прямая лежит на плоскости.
Пример 3. Определить взаимное расположение прямой
2x + y +z +1 = 0
L : и плоскости σ: x − y + 2z + 2 = 0 .
5x + y +4z −2 = 0
2x + y +z +1 = 0
Решение. Решим систему 5x + y +4z −2 = 0 .
x −y +2z +2 = 0
К третьему уравнению прибавим первое. Получаем
2x + y +z +1 = 0 |
|
2x + y +1−x +1 = 0 |
||
|
5x + y +4z −2 = 0 |
или |
|
5x + y +4(1−x) −2 = 0 |
|
|
|||
|
3x +3z +3 = 0 |
|
|
z = −1−x |
|
|
|
||
|
|
128 |
|
|
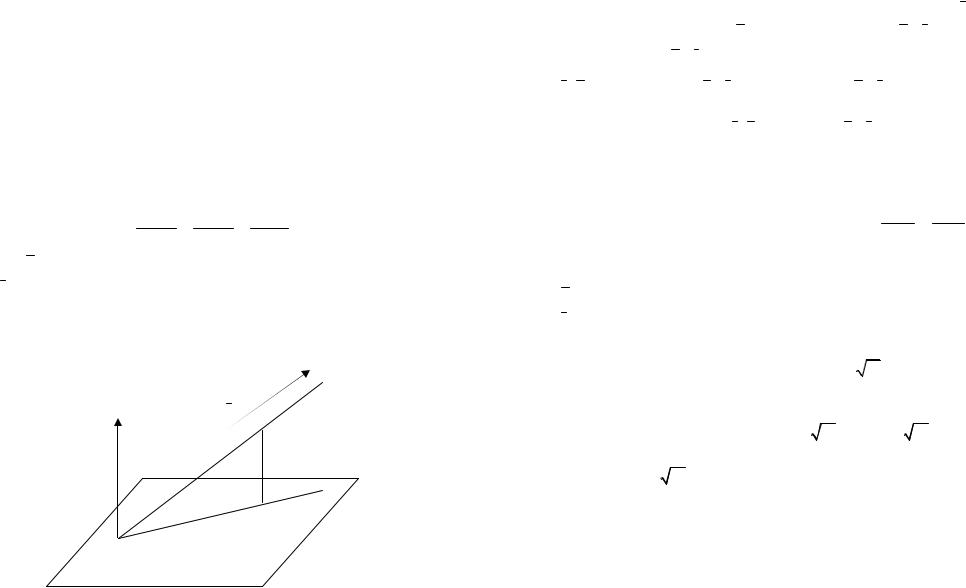
x + y = −2 |
|
или x + y = −2 |
. Система имеет бесконечно много реше- |
|
|
z = −1−x |
|
ний (x, −2 − x, −1− x), x R .
Ответ: прямая лежит на плоскости.
Задача 152. Найти угол между прямой и плоскостью.
Решение. Пусть плоскость α задана общим уравнением
α: Ax +By +Cz + D = 0 ,
апрямая L задана каноническим уравнением
L : x −mxo = y −nyo = z −pzo ,
где n = (A, B, C) – нормальный вектор плоскости α, s = (m, n, p) – направляющий вектор прямой L.
Определение. Углом между прямой и плоскостью называется острый угол между прямой и ее проекцией на эту плоскость.
s
|
|
|
L |
n |
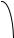 ϕ
ϕ
α
Рис. 51. 129
Обозначим угол между направляющим вектором прямой s и нормальным вектором n плоскости α через (n ^ s) . Тогда, если угол (n ^ s) острый, т.е. скалярное произведение
s n > 0 , то ϕ = π2 −(n ^ s) ; если же угол (n ^ s) тупой, т.е.
скалярное произведение s n < 0 , то ϕ = (n ^ s) − π2 . То есть,
в любом случае ϕ = |
|
π |
|
|
|
|
. |
|
|
|
|
|
|
|
|||
−(n |
^ s) |
|||||||
|
|
2 |
|
|
|
|
|
|
Пример. Найти угол между прямой L : x + 4 = y−−17 = z −3 2 и плоскостью σ: 2x −2y + z +6 = 0 .
Решение. Вычисляем угол между нормальным вектором n = (2; −2;1) плоскости и направляющим вектором прямой s = (1;−1;3) :
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
n |
|
s |
|
|
= arccos |
|
7 |
. |
|
|
|
||||||
(n |
s) = arccos |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| n | | s | |
|
|
|
3 |
11 |
|
|
|
|
|||||||||
Искомый угол между прямой и плоскостью равен |
|
|
|||||||||||||||||||||||||||||
(L ^ σ) = |
π |
|
|
|
|
|
|
π |
−arccos |
|
7 |
= arcsin |
|
7 |
. |
||||||||||||||||
−(n |
^ s) = |
||||||||||||||||||||||||||||||
2 |
2 |
|
11 |
|
11 |
||||||||||||||||||||||||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|||||||||||||
Ответ: arcsin |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 153. Найти точку встречи прямой с плоскостью.
Решение. Решение задачи вытекает из теоремы, сформулированной в предыдущей задаче.
Пусть плоскость α задана общим уравнением
α: Ax +By +Cz + D = 0 ,
апрямая L задана параметрическими уравнениями
130
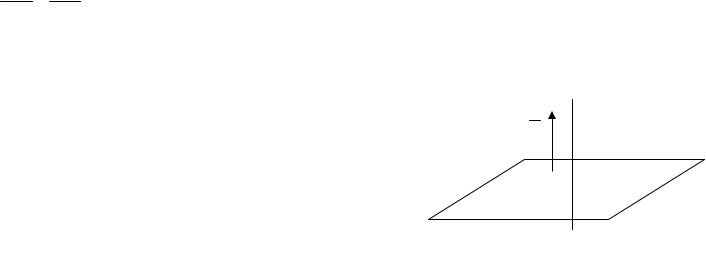
|
x = xo +mt |
|
L : |
|
y = yo +nt , t R . |
|
||
|
|
z = zo +pt |
|
|
|
Подставляем х, у и z из параметрических уравнений в уравнение плоскости:
A (xo +mt) +B(yo +nt) +C(zo +pt) +D = 0 .
Решаем это уравнение относительно t. Если прямая пересекается с плоскостью, то данное уравнение имеет единственное решение.
Подставляем найденное значение t в параметрические уравнения и вычисляем координаты искомой точки.
Пример 1. Найти точку встречи прямой
L : x +4 = y−−17 = z −3 2
с плоскостью σ: 2x −2y + z +6 = 0 .
Решение. Запишем параметрические уравнения данной прямой:
x = −4 + t |
|
|
y = 7 −t , t R . |
L : |
|
|
z = 2 +3t |
|
|
Подставляем x = t −4, y = 7 − t, z = 2 +3t в уравнение плос-
кости: 2(t − 4) − 2(7 − t) + 2 + 3t + 6 = 0 .
Решаем это уравнение и находим t = −2 . Подставляем это значение t в параметрические уравнения прямой:
|
x = −4 |
−2 |
= −6 |
|
y = 7 |
+2 |
= 9 . |
|
z = 2 +3 (−2) = −4
Ответ: (– 6; 9; – 4).
131
Пример 2. Убедиться, что прямая
2x + y +z +1 = 0 L : 5x + y +4z −2 = 0
пересекает плоскость σ: 2x −2y + z +5 = 0 , и найти коор-
динаты точки пересечения. Решение. Решим систему
2x + y +z +1 = 0
5x + y +4z −2 = 0 .2x +2y +z +5 = 0
Из третьего уравнения вычтем первое. Получаем y = −4 .
2x +z = 3
Подставляем у в первое и второе уравнения: .
5x +4z = 6
|
z = 3 − 2x |
или |
z = 3 −2x |
, или |
x = 2 |
. |
||
Отсюда, |
+ 4(3 −2x) = 6 |
|
−3x |
= −6 |
|
|||
5x |
|
|
|
z = −1 |
|
|||
Ответ: (2; – 4; – 1).
Задача 154. Найти проекцию точки на плоскость.
Mo
n
M1
α
L
Рис. 52.
Решение. Пусть дана точка Mo (xo , yo , zo ) и плоскость
α: Ax +By +Cz + D = 0 . 132
Проведем через точку Mo прямую L перпендикулярно данной плоскости α и найдем их точку встречи M1 (x1 , y1 , z1 ) = L ∩α. Точка M1 будет искомой проекцией точки Mo на плоскость α.
Из построения следует, что нормальный вектор n плоскости α является в то же время направляющим вектором прямойL. Пишем параметрическое уравнение прямой L:
|
x = xo +At |
||
L : |
|
|
+Bt , t R . |
y = yo |
|||
|
|
z = zo |
+Ct |
|
|
||
Осталось, как в предыдущей задаче, найти точку встречи M1 прямой L с плоскостью α, т.е. решить систему уравнений:
Ax +By +Cz +D = 0 |
|
|
|
x = xo +At |
|
|
, t R . |
|
|
y = yo +Bt |
|
|
|
|
|
z = zo +Ct |
|
|
|
|
Замечание. Попутно мы решили задачу: через данную точку провести прямую перпендикулярно данной плоскости.
Пример. Найти проекцию точки P(1; 2; −3) на плоскость x + y − z + 6 = 0 .
Решение. Составляем и решаем систему уравнений:
|
x =1 |
+ t |
|
|
y = 2 |
+ t |
|
|
, t R . |
||
|
z = −3 −t |
||
|
|
||
|
|
|
|
x + y −z +6 = 0 |
|
||
Подставляем х, у, z из первых трех уравнений в четвертое: 133
1 + t + 2 + t +3 + t + 6 = 0, t = −4 , x = −3, y = −2, z =1. Ответ: (−3;−2;1) .
Задача 155. Найти точку симметричную данной относительно плоскости.
Решение. Пусть дана точка Mo (xo , yo , zo ) и плоскость
α: Ax +By +Cz + D = 0 .
Сначала, как в предыдущей задаче, находим проекцию M1 (x1 , y1 ,z1 ) точки Mo (xo , yo , zo ) на плоскость α. Иско-
мая точка M2 (x2 , y2 ,z2 ) является концом отрезка Mo M2 , для которого точка M1 является его серединой. Ситуация схематически изображена на следующем рисунке:
Mo
α
M1
M2
Рис. 53.
Для вычисления координат точки M2 используем формулы середины отрезка.
Пример. Найти точку симметричную точке P(1; 2; −3) относительно плоскости x + y − z + 6 = 0 .
Решение. Проекцию точки Р на данную плоскость мы уже нашли (см. пример предыдущей задачи). Обозначим эту точку через S(−3; −2;1) . Пусть Q(x, y, z) – искомая точка.
Тогда в векторной форме:
|
= |
|
rP |
+ |
rQ |
или |
|
= 2 |
|
− |
|
, |
r |
|
r |
r |
r |
||||||||
|
|
|
|
|||||||||
S |
2 |
|
|
Q |
|
S |
|
P |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
134 |
|
|
|
|
|
|

где rP , rS , rQ – радиус-векторы точек P, S, Q:
|
P |
|
|
|
S |
|
|
Q |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rS |
|
|
|
|
|||
|
rP |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rQ |
||||
|
|
|
|
|
|
|
||||
О
Рис. 54.
Координаты точки Q удобнее вычислять, записывая их не в строчку, а в столбец:
xy =z
Ответ: (−7; −6;5)
|
|
|
|
|
−3 |
|
1 |
|
−7 |
||||||
2 |
|
− |
|
= 2 |
|
−2 |
|
− |
|
2 |
|
= |
|
−6 |
. |
r |
r |
||||||||||||||
|
S |
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 156. Найти расстояние между параллельными прямой и плоскостью.
Решение. Пусть прямая L параллельна плоскости α.
L : |
x −xo |
= |
y − yo |
= |
z −zo |
, |
α: Ax + By +Cz + D = 0 . |
m |
n |
|
|||||
|
|
|
p |
|
|||
Тогда расстояние между ними равно расстоянию от точки Mo (xo , yo , zo ) L до плоскости α:
d (L, α) = d (Mo , α) .
Таким образом, данная задача сводится к задаче 129. Однако можно решать эту задачу и задачу 129 по-другому.
Найдем, как в задаче 154, проекцию M1 (x1 , y1 ,z1 ) точки Mo (xo , yo , zo ) L на плоскость α и тогда
135
d (L, α) = MoM1 = (x −x1)2 +(y −y1)2 +(z −z1)2 .
Пример. Убедиться, что прямая L : x +4 = |
y −7 |
= |
z − |
2 |
−1 |
|
|
||
|
3 |
|
||
параллельна плоскости σ: x + y +1 = 0 , и найти расстояние
между ними.
Решение. Вычисляем скалярное произведение направляющего вектора данной прямой и нормального вектора данной плоскости:
s = (1, −1, 3) , n = (1, 1, 0) и s n =1−1 = 0 .
Так как скалярное произведение равно нулю, то s n и, следовательно, либо прямая лежит на плоскости, либо она параллельна ей. Так как Mo (−4;7;2) σ, то имеет место
второй случай, т.е. L || σ.
Искомое расстояние можно найти двумя способами.
1-й способ. Через точку Mo (−4, 7, 2) L проводим прямую
L σ: |
L : |
x +4 |
= |
y −7 |
= z −2 , |
|
|
||||
1 |
1 |
1 |
1 |
0 |
|
|
|
||||
где s1 = n = (1, 1, 0) || L1 – направляющий вектор L1 . Находим параметрические уравнения L1 и подставляем их в уравнение плоскости:
|
|
x = −4 + t |
|||
|
L1 : |
|
y = 7 + t |
, −4 + t +7 + t +1 = 0 , откуда t = −2 и |
|
|
|
||||
|
|
|
z = 2 |
|
|
|
|
|
|
||
x = −4 −2 |
= −6 |
|
|||
|
y = 7 |
−2 |
=5 |
– координаты точки M1 = L1 ∩σ. |
|
|
|||||
|
|
z |
= 2 |
|
|
|
|
|
|
||
|
|
|
|
|
136 |

Теперь, расстояние d от прямой L до плоскости σ равно длине отрезка Mo M1 :
d = M M = (−6 +4)2 |
+(5 −7)2 |
+(2 −2)2 |
= 2 2 . |
o 1 |
|
|
|
2-й способ. Искомое расстояние d можно найти по формуле расстояния от точки до плоскости:
d = |
| Axo |
+ Byo |
+ Czo |
+ D | |
= |
|1 (−4) +1 7 + 0 2 +1| |
= 2 2 . |
|
A2 + B2 + C2 |
12 +12 + 02 |
|||||
|
|
|
|
||||
Ответ: 2 |
2 . |
|
|
|
|
|
|
Задача 157. Найти уравнение пучка плоскостей с заданной осью пучка.
Решение. Пусть ось пучка задана каноническим уравнением:
L : x −mxo = y −nyo = z −pzo
Запишем каноническое уравнение данной прямой в виде равносильной системы:
|
|
x −x |
o |
|
= |
|
y − y |
o |
|
||
|
|
|
|
|
|
|
|
||||
|
|
m |
|
|
n |
|
|
|
|||
L : |
|
|
|
|
|
|
|
|
. |
||
|
|
y −yo |
|
|
z −zo |
|
|||||
|
|
|
= |
|
|
|
|||||
|
|
|
n |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Каждое уравнение этой системы есть уравнение плоскости:
L : |
nx −my +(myo |
−nxo ) = 0 |
. |
|
|
py −nz +(nzo −pyo ) = 0 |
|||
|
|
|
||
Ясно, что последняя система равносильна каноническим уравнениям, следовательно, мы имеем две плоскости из искомого пучка плоскостей, причем эти плоскости пересекаются по данной прямой, т.е. любое решение последней системы есть координаты точки, лежащей на прямой L, и,
137
обратно, координаты любой точки, лежащей на прямой L, удовлетворяют обоим уравнения системы. В соответствии с теорией, уравнение искомого пучка плоскостей имеет вид:
α(nx −my +myo −nxo ) +β(py −nz +nzo −pyo ) = 0 .
Пример. Найти уравнение пучка плоскостей с осью пучка
L : x−−32 = y6+1 = z +2 3 .
Решение. Запишем канонические уравнения данной прямой в виде системы:
x −2 |
= |
y +1 |
|
|
6x |
+3y −9 |
= 0 |
|
2x |
+ y −3 |
= 0 |
|
||||
|
−3 |
|
|
|
|
|||||||||||
|
6 |
|
или |
, или |
. |
|||||||||||
|
|
|
|
−6z −16 |
= 0 |
|
|
−8 |
= 0 |
|||||||
|
y +1 |
= |
z +3 |
|
2y |
|
y −3z |
|
||||||||
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
α(2x + y −3) +β(y −3z −8) = 0 . |
|
|
|
|
|
||||||||||
Задача 158. Определить взаимное расположение двух прямых в пространстве, одна из которых или обе заданы в виде пересечения двух плоскостей.
Решение. 1) Пусть одна прямая задана в канонической форме, другая в виде пересечения двух плоскостей:
L1 : |
x − x |
1 |
|
y − y |
|
z −z |
|
A1x + B1 y +C1z + D1 |
= 0 |
|
|
|
= |
1 |
= |
1 |
, |
L2 |
: |
= 0 |
. |
||
m1 |
|
n1 |
|
||||||||
|
|
|
|
p1 |
|
A2 x + B2 y +C2 z + D2 |
|
||||
Запишем уравнения прямой L1 в параметрической форме и решим систему:
|
|
|
x = x1 +mt |
|
|
|
||
|
|
|
y = y1 +nt |
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
z = z1 +pt |
|
. |
(1) |
||
|
|
|
|
|||||
|
A x +B y +C z +D |
|
= 0 |
|
||||
|
1 |
1 |
1 |
1 |
= 0 |
|
||
A |
x +B |
y +C |
z +D |
2 |
|
|||
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
138 |
|
|
|
|
Исключаем переменные х, у, z, подставляя их из первых трех уравнений системы в четвертое и пятое уравнения:
A1 (x1 +mt) +B1(y1 +nt) +C1 (z1 +pt) +D1 = 0A2 (x1 +mt) +B2 (y1 +nt) +C2 (z1 +pt) +D2 = 0
и решаем каждое уравнение этой системы:
a |
t = b |
(2) |
1 |
1 |
|
a2t = b2 |
|
|
Если эта система имеет единственное решение t = t0 ,
то, подставляя его в первые три уравнения системы (1), находим точку пересечения данных прямых.
Если каждое уравнение системы (2) верно при любых значениях параметра t, т.е. a1 = a2 = b1 = b2 = 0 , то прямые
совпадают.
Если каждое уравнение системы (2) не имеет решений, т.е. a1 = a2 = 0, b1 ≠ 0 ≠ b2 , то прямые параллельные.
Во всех остальных случаях прямые скрещивающиеся.
Пример 1. Определить взаимное расположение двухпрямых:
|
|
y −7 |
= z −2 |
и |
|
x +3y −z = 0 |
|
. |
|
|||
L1 |
: x +4 = |
L2 : |
|
|
|
|
|
|
||||
−1 |
|
|
|
|
|
|
||||||
|
|
3 |
|
2x −y +z −4 = 0 |
|
|
||||||
Решение. Запишем параметрические уравнения прямой L |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
и подставим их в уравнения прямой L2 : |
|
|
|
|
|
|
|
|||||
|
x = −4 + t |
|
t −4 +3(7 −t) −(2 +3t) = 0 |
|
|
|
||||||
L1 : |
|
|
|
. |
||||||||
y = 7 −t , |
L2 : |
|
|
|
|
|
|
0 |
||||
|
|
2(t −4) −(7 −t) +2 +3t −4 = |
|
|||||||||
|
z = 2 +3t |
|
|
|
|
|
|
|
|
|
|
|
Решая |
последнюю |
систему, |
получаем |
t |
= |
3 |
. Отсюда |
|||||
|
= |
17 |
||||||||||
|
|
|
|
|
|
6t |
|
|
|
|
||
следует, что прямые не пересекаются, так как система не
139
имеет решений, не параллельные, ибо в противном случае каждое уравнение системы не имело бы решений, а следовательно, прямые скрещивающиеся.
Ответ: прямые скрещивающиеся.
2) Пусть теперь обе прямые заданы в виде пересечения двух плоскостей:
|
A x +B y +C z +D = 0 |
, |
|
A |
x +B y +C |
z +D |
|
= 0 |
. |
|
1 1 1 1 |
|
3 |
3 3 |
|
3 |
|
||
A2x +B2 y +C2z +D2 = 0 |
|
A4x +B4 y +C4z +D4 = 0 |
|
||||||
Решим систему изчетырехуравнений с тремя неизвестными:
|
A x +B y +C z +D = 0 |
|
||||||
|
1 |
1 |
1 |
1 |
|
|
||
|
A2x +B2 y +C2z +D2 = 0 |
|
||||||
|
A |
x +B y +C |
3 |
z +D |
3 |
= 0 . |
(2) |
|
|
3 |
3 |
|
|
|
|
||
|
A4x +B4 y +C4z +D4 = 0 |
|
||||||
|
|
|||||||
Если система имеет единственное решение, то прямые пересекаются в точке, координаты которой являются решением системы.
Если система допускает бесконечное множество решений, то прямые совпадают.
Если система не имеет решений, то прямые скрещивающиеся или параллельные. Найдем каноническое уравнение одной из прямых. Тогда вопрос решается как в предыдущем случае.
Пример 2. Определить взаимное расположение двух пря-
мых: |
L1 : |
2x + y +z −1 = 0 |
и |
L2 : |
x +z −1 = 0 |
. |
||||
|
5x |
+ y +4z −4 |
= 0 |
|
x + y = 0 |
|||||
|
|
|
|
|
|
|
||||
Решение. Решаем систему
140
