
методичка + кр по теории вероятности
.pdfЗадача 2.
Электролампы изготавливаются на трех заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа стандартная.
Решение.
А = {купленная в магазине лампа стандартная}, Н1 = {лампа с первого завода}, Н2 = {лампа со второго завода}, Н3 = {лампа с третьего завода}.
Р(Н1) = 0,45; Р(Н2) = 0,4; Р(Н3) = 0,15.
Р(А/Н1) = 0,7; Р(А/Н2) = 0,8; Р(А/Н3) = 0,81.
P( A) = 0,45× 0,7 + 0,4× 0,8 + 0,15× 0,81 = 0,7565.
Задача 3.
Агентство по страхованию автомобилей разделяет водителей по трем классам: 1 класс – мало рискуют, 2 класс – рискуют средне, 3 класс – сильно рискуют. Из всех водителей, застраховавших автомобили, 30% принадлежат к классу 1, 50% - к классу 2 и 20% - к классу 3. Вероятность того, что в течение года водитель класса 1 попадет хотя бы в одну аварию, равна 0,01; для водителя класса 2 вероятность равна 0,02; для водителя третьего класса – 0,08. Водитель страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу 1? К классу 2? К классу 3?
Решение.
А = {водитель попадает в аварию}. Н1 = {водитель относится к 1 классу}, Н2 = {водитель относится к 2 классу}, Н3 = {водитель относится к 3 классу}. Р(Н1) = 0,3; Р(Н2) = 0,5; Р(Н3) = 0,2;
Р(А/Н1) = 0,01; Р(А/Н2) = 0,02; Р(А/Н3) = 0,08;
P( A) = 0,3× 0,01+ 0,5× 0,02 + 0,2× 0,08 = 0,029 .
По формуле Байеса пересчитаем вероятности гипотез, после того, как событие А произошло:
P(H1 | A) = |
0,3× 0,01 |
» 0,1035 ; |
|
|
|
0,029 |
|
P(H 2 |
| A) = |
0,5× 0,02 |
» 0,3448 ; |
|
|
0,029 |
|
P(H3 |
| A) = |
0,2× 0,08 |
» 0,5517 . |
|
|
0,029 |
|
11

6. Формула Бернулли.
Рассматривается последовательность независимых испытаний, в каждом из которых вероятность наступления события А одинакова и равна р (условно это событие
рассматривается как успех, а его ненаступления ( A ) как неудача, причем p( A) = 1- p = q ).
Вероятность того, что в n испытаниях успех наступит ровно m раз, обозначим через
Pn(m).
Имеет место формула Бернулли:
Pn (m) = Cnm p m q n− m .
Задача 1.
Что вероятнее выиграть у равносильного противника а) три партии из четырех или пять партий из восьми? б) не менее трех партий из четырех или не менее пяти партий из восьми?
Решение.
Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = ½.
а) Найдем вероятность выигрыша трех партий из четырех:
P (3) = C 3 |
× |
æ |
1 ö |
3 × |
æ 1 |
ö 1 |
= 1 . |
|
|
|
|
|
|
|
|
||||
4 |
4 |
|
ç |
÷ |
|
ç |
÷ |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
è |
2 ø |
|
è 2 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, P (5) = |
C 5 |
× |
æ |
1 |
ö 5 |
× |
æ |
1 |
ö 3 |
= |
7 |
. |
|||||||
ç |
|
÷ |
ç |
|
÷ |
|
|||||||||||||
|
|
|
|
|
8 |
|
|
8 |
|
2 |
|
2 |
|
32 |
|
||||
|
1 |
|
|
7 |
|
|
|
|
|
è |
ø |
|
è |
ø |
|
|
|||
Так как |
> |
|
, то вероятнее выиграть три партии из четырех. |
||||||||||||||||
4 |
|
32 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) Вероятность выиграть не менее 3-хпартий их четырех (обозначим ее R4 (3) ). R4 (3) = P4 (3) + P4 (4) = 14 + 161 = 165 ;
Вероятность выиграть не менее пяти партий из восьми ( R8 (5) ):
R8 (5) = P8 (5) + P8 (6) + P8 (7) + P8 (8) = 25693 .
Так как 25693 > 165 , то вероятнее выиграть не менее пяти партий из восьми.
Задача 2.
Всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из семи посеянных семян взойдут пять?
Решение.
Вероятность всхожести отдельно взятого семени р=0,9; q=1-0,9=0,1. По формуле Бернулли:
P7 (5) = C75 p5 q 2 = C75 × (0,9)5 × (0,1)2 = 0,124 .
Таким образом, в среднем в 124 случаях из 1000 из 7 посеянных семян взойдут 5.
12

7. Дискретные и непрерывные случайные величины.
Величина, которая в зависимости от случай принимает различные числовые значения, называется случайной. Обозначаются они буквами Х, У и т.п.
Вероятность того, что случайная величина Х примет значение, меньшее х, называется функцией распределения случайной величины Х:
F(x)=P(X<x).
Основные свойства функции распределения: 1. Если a<b, то P(a ≤ X < b) = F(b) − F(a) .
2.Функция распределения – неубывающая функция.
3.Функция распределения непрерывна слева, то есть
|
|
|
lim F( x) = F(a) . |
|
|
|
|
x→ a− |
0 |
4. |
lim F( x) = 1 |
; |
lim F( x) = 0. |
|
|
x→ + ∞ |
|
x→ − ∞ |
|
7.1. Дискретная случайная величина.
Случайная величина называется дискретной, если ее значения можно перенумеровать.
Функция распределения дискретной случайной величины определяется посредством
равенства: F( x) = å pi , где суммирование распространяется на все индексы, для которых
i
xi<x.
Дискретная случайная величина может быть задана: 1) рядом распределения, 2) многоугольником распределения, 3) функцией распределения.
Рядом распределения называется совокупность всех частных значений, которые принимает случайная величина xi, и соответствующих им вероятностей pi = P{X = xi } . Ряд распределения обычно задается в виде таблицы:
Х |
|
х1 |
x2 |
… |
xn |
… |
Р |
|
Р1 |
р2 |
… |
pn |
… |
å |
pi = 1. |
|
|
|
|
|
i |
|
|
|
|
|
|
Многоугольником распределения называется графическое изображение ряда. |
||||||
Откладываются точки Ai ( xi , pi ) |
и соединяются ломанной. |
|
|
|||
Напоминаем схему решения задач на построение законов распределения.
1)Необходимо обозначить и описать случайную величину, о которой идет речь в задаче.
2)Описать множество ее возможных значений xi.
3)Рассмотреть каждое из событий {X=xi}, i=1,2,…, n.
4)Вычислить вероятность каждого из событий {X=xi} с помощью основных теорем и формул.
5) Проверить правильность составленного распределения с помощью равенства
ån pi = 1. i= 1
13
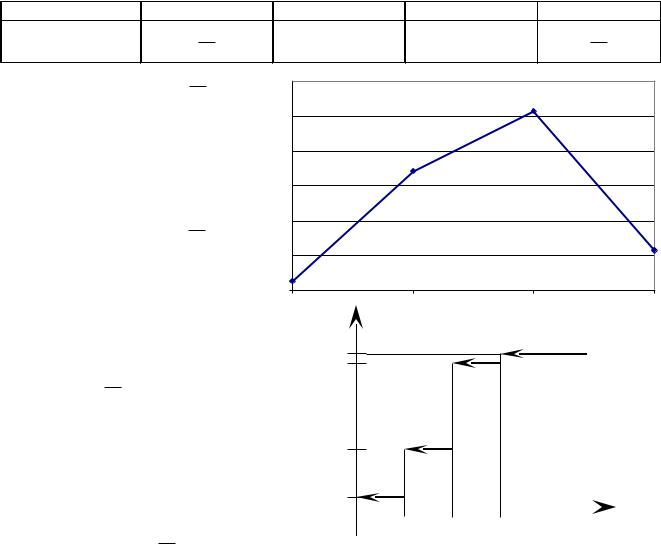
Задача 1.
В урне 7 шаров, из которых 4 белых, а остальные черные. Из урны наудачу извлекаются 3 шара. Х – число извлеченных белых шаров. Найти а) закон распределения;
б) построить многоугольник распределения; в) найти и F(x); г)Найти вероятность
события X ³ 2 .
Решение.
Возможные значения случайной величины Х: 0, 1, 2, 3. Заполняем таблицу:
Х |
|
|
|
|
|
0 |
|
1 |
|
|
2 |
3 |
|
Р |
|
|
|
|
|
1 |
|
12 |
|
|
18 |
4 |
|
|
|
C40 × C33 |
|
|
35 |
|
35 |
|
|
35 |
35 |
||
P{X = 0} = |
|
= |
1 |
, |
|
3/5 |
|
|
|
|
|||
C73 |
|
35 |
|
1/2 |
|
|
|
18/35 |
|||||
P{X = 1} = |
C41 × C32 |
|
|
12 |
|
|
|
|
|
||||
= |
, |
|
|
|
|
|
|||||||
C73 |
35 |
|
2/5 |
|
|
|
|
||||||
P{X = 2} = |
C42 × C31 |
|
= |
18 |
, |
P |
3/10 |
|
12/35 |
|
|
||
C73 |
|
35 |
|
|
|
|
|||||||
P{X = 3} = |
C43 × C30 |
|
= |
4 |
|
|
1/5 |
|
|
|
|
||
C 3 |
|
35 . |
|
|
|
|
|
4/35 |
|||||
|
|
7 |
|
|
|
|
|
1/10 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
3 |
Найдем F(x). |
|
|
|
|
|
|
F(x) |
|
|
X |
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|||
ì |
0, x £ |
0; |
|
|
|
|
|
|
|
|
|
||
ï |
1 |
,0 < |
x £ |
1; |
|
|
|
31/35 |
|
|
|
|
|
ï |
35 |
|
|
|
|
|
|
|
|
||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
F( x) = íï |
13 |
,1 < x £ 2; |
|
|
|
|
|
|
|
|
|||
ï |
35 |
|
|
|
|
|
|
|
13/35 |
|
|
|
|
ï |
31 |
,2 < |
x £ |
|
3; |
|
|
|
|
|
|
||
ï |
35 |
|
|
|
|
|
|
|
|
||||
ï |
1, x > |
3. |
|
|
|
|
|
1/35 |
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
||||
P{ X ³ 2} = |
18 + |
4 |
|
|
22 . |
|
0 |
1 |
2 |
3 |
x |
||
|
= |
|
|
|
|
|
|
||||||
|
|
35 |
35 |
|
35 |
|
|
|
|
|
|
||
Задача 2.
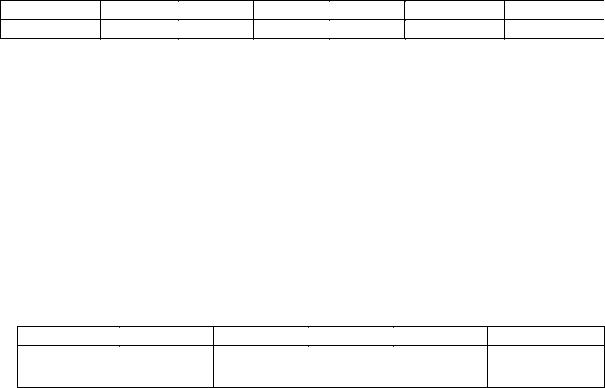
Пусть ведется стрельба по цели до первого попадания с конечным запасом «k». Пусть Х – число израсходованных патронов до первого попадания. Составить закон распределения случайной величины Х.
14
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
1 |
|
2 |
3 |
… |
k-1 |
k |
P |
|
p |
|
qp |
q2p |
|
qk-2p |
qk-1p+qk |
P{ X = 1} = |
p; |
|
|
|
|
|
|
|
P{ X = 2} = q × p; |
|
|
|
|
|
|
||
P{ X = 3} = q2 × p; |
|
|
|
|
|
|
||
… |
|
|
|
|
|
|
|
|
P{ X = k - 1} = qk − 2 × p. |
|
|
|
|
||||
Событие { X = k} |
означает, что израсходован весь запас патронов. |
|
||||||
P{ X = k} = qk − 1 × p + q k .
Задача 3.
Имеется 5 ключей, из которых только один подходит к замку. Найти закон распределения случайной величины Х – числа проб при открывании замка, если испробованный ключ в следующих опробываниях не участвует.
Решение.
Х |
|
|
|
|
1 |
|
|
|
|
2 |
3 |
4 |
5 |
Р |
|
|
|
|
1 |
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
5 |
|
|
|
|
5 |
5 |
5 |
5 |
P{ X = 1} = |
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
P{ X = 2} = |
4 |
× |
1 |
= 1 |
; |
|
|
|
|
|
|
||
|
5 |
|
4 |
|
5 |
|
|
|
|
|
|
|
|
P{ X = 3} = |
4 |
× |
3 |
× |
1 |
= |
1 ; |
|
|
|
|
|
|
|
5 |
|
4 |
|
3 |
|
5 |
|
|
|
|
|
|
P{ X = 4} = |
4 |
× |
3 |
× |
2 |
× |
1 |
= |
1 |
; |
|
|
|
|
5 |
|
4 |
|
3 |
|
2 |
|
5 |
|
|
|
|
P{ X = 5} = |
4 |
× |
3 |
× |
2 |
× |
1 |
×1 = |
1 . |
|
|
|
|
|
5 |
|
4 |
|
3 |
|
2 |
|
|
5 |
|
|
|
7.2. Непрерывная случайная величина.
Непрерывной случайной величиной называется такая величина, которая может принимать любые числовые значения из некоторого интервала (конечного и бесконечного). Задать ее можно с помощью функции распределения F(x) или плотности распределения f(x) (дифференциальной функции распределения). Дифференциальной
функцией распределения f(x) называется функция |
f ( x) = lim |
P( x < |
X < x + x) |
. |
|
|
|||
|
x→ 0 |
D x |
||
График функции f(x) называется кривой распределения.
15

Свойства дифференциальной функции распределения.
1. f ( x) ³ 0 для любого х.
β
2. P(α < X < β ) = ò f ( x)dx (см. рис.).
α
f(x)
|
|
|
|
|
x |
|
|
|
|
|
|
|
+ò∞ |
|
α |
β |
|
|
|
|
|||
3. |
f ( x)dx = 1. |
|
|
||
−∞
4.Связь между дифференциальной и интегральной функциями распределения:
F( x) = òx f (t)dt ,
− ∞
F ′( x) = f ( x) , если в точке х функция f(x) непрерывна.
Пример непрерывного распределения.
Равномерное распределение.
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность вероятности случайной величины постоянна, то есть
ì |
0, x < |
a; |
f ( x) = íï c, a £ x £ b; |
||
ï |
0, x > |
b. |
î |
||
Найдем параметр с. Так как +ò∞ f ( x)dx = 1, то имеем:
|
− ∞ |
|
òa 0× dx + òb c × dx + |
+ò∞ 0× dx = 1; |
|
− ∞ |
a |
b |
Следовательно, c = Таким образом,
с(b-a)=1,
1 . b - a
ì |
|
0, x |
|
f ( x) = íï |
1 |
|
, a |
|
a |
||
ï b - |
|
||
î |
|
0, x |
|
<a;
£x £ b;
>b.
16
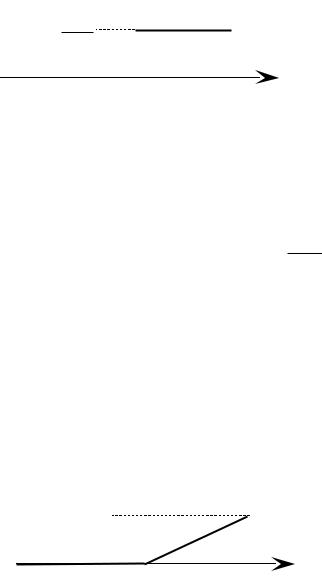
Построим график f(x).
f(x)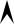
1
b − a
|
|
a |
b |
x |
Найдем функцию распределения F(x): |
|
|
||
F( x) = òx f ( x)dx .
− ∞
Если x<a, то F( x) |
= |
òx |
0 × dx = |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
x |
1 |
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
Если a £ x £ b , то F( x) = ò 0 × dx + |
ò |
|
|
|
|
|
× dx = |
|
|
x |
||||||||
|
|
b - |
a |
b - a |
||||||||||||||
Если x>b, то F( x) |
|
a |
− ∞ |
b |
1 |
a |
|
|
|
x |
|
|
|
|
||||
= |
0× dx + |
|
|
× dx + |
0× dx = 1. |
|||||||||||||
ò |
ò |
b - |
a |
ò |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, |
|
− ∞ |
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
||
|
|
|
|
|
|
|
|
ì |
|
0, x < |
a; |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
F( x) = íï |
x - a |
, a £ x £ b; |
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ï b - |
a |
|
b. |
||||||
|
|
|
|
|
|
|
|
|
î |
|
1, x > |
|||||||
График F(x) представим на рисунке:
x
a
=x - a . b - a
F(x)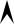
|
|
1 |
|
x |
|
|
|
||
|
|
a |
b |
|
Задача 1. |
f ( x) = íì |
0, x < 0; |
|
|
Дана функция |
|
|
||
|
î |
Cxe− x , x ³ 0. |
|
|
При каком С она является плотностью вероятности?
Решение.
Во-первых, f ( x) ³ 0 , если f(x) – плотность вероятности, то есть C ³ 0 . Во-вторых, +ò∞ f ( x)dx = 1.
− ∞
17

0 |
|
|
+ ∞ |
|
+ ∞ |
A |
|
ç |
|
|
A |
÷ |
|
|
. |
ò |
|
|
ò |
|
ò |
|
|
|
|
|
|||||
|
0 |
× dx + |
|
Cxe− x dx = C |
|
xe− x dx = C lim |
æ |
- |
A |
- e− A + 1ö |
= |
C = 1 |
|
||
|
|
|
|
e |
|
|
|||||||||
− ∞ |
|
|
0 |
|
0 |
|
→ ∞ |
è |
|
|
ø |
|
|
|
|
Ответ: С=1.
8. Числовые характеристики случайной величины.
Пусть Х – случайная дискретная величина, закон распределения которой имеет вид:
X |
x1 |
x2 |
… |
xk |
… |
xn |
P |
p1 |
p2 |
… |
pk |
… |
pn |
Математическим |
ожиданием |
МХ случайной |
величины |
Х |
называется сумма |
|
произведений значений случайной величины на вероятности, с которыми она принимает эти значения:
MX = ån xi pi .
i= 1
Математическим ожиданием непрерывной случайной величины с плотностью f(x) называется
MX = +ò∞ x × f ( x) × dx ,
− ∞
при условии, что интеграл сходится.
Свойства математического ожидания.
1.M[C]=C, где С – постоянная.
2.M[CX]=CM[X], где С – постоянная.
3.M[X1+X2+…+Xn]=M[X1]+M[X2]+…+M[Xn].
4.Если - независимы, то M[X1×X2×…×Xn]=M[X1] ×M[X2] ×…×M[Xn]. Дисперсией случайной величины Х называется число DX
DX=M[(X-MX)2].
Число σ ( x) = 
 DX называется средним квадратическим отклонением случайной
DX называется средним квадратическим отклонением случайной
величины Х.
Справедлива формула
DX=M[X2]-(M[X])2 (*), Этой формулой удобно пользоваться на практике.
Формула нахождения дисперсии для дискретной случайной величины
DX = å (xi - MX )2 pi ,
i
или с учетом формулы (*):
DX = å xi2 pi - (MX ) 2 .
i
Формула нахождения дисперсии непрерывной случайной величины:
DX = +ò∞ ( x - MX ) 2 f ( x) × dx , или
− ∞
18

DX = +ò∞ x 2 f ( x) × dx - (MX ) 2 .
− ∞
Свойства дисперсии.
1.D[C]=0, где С – постоянная.
2.D[CX]=C2D[X], где С – постоянная.
3.D[X ± Y]=D[X] + D[Y], где X, Y – независимые случайные величины.
Задача 1.
Случайная величина Х задана плотностью f(x):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
0, x £ 0; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x) = íï |
2x,0 < x < 1; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
0, x ³ 1. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|||
Найти MX, DX, σX. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
MX = |
+ò∞ x × f ( x) × dx = ò1 |
x × 2x × dx = |
2x3 |
|
= |
2 , |
||||||||||||||||||
|
||||||||||||||||||||||||
|
− ∞ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
0 |
|
3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
DX = M [X 2 ]- (M [X ])2 , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
M [X 2 ] = ò1 x2 × 2x × dx = |
x4 |
|
1 |
= |
1 |
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
DX = |
1 - |
4 |
= |
9 − 8 = |
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|||||||
9 |
18 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
σ X = |
|
1 |
|
= |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 2.
Пусть задан закон распределения некоторой случайной величины Х:
Х |
|
2 |
4 |
Р |
|
0,6 |
0,4 |
Найти МХ и DX. |
|
||
Решение. |
|
|
|
MX = å xi |
pi = 2× 0,6 + 4× 0,4 = 2,8. |
|
|
i |
|
|
|
DX = M [X 2 ]- (M [X ])2
Напишем закон распределения случайной величины Х2:
19
Х2 |
4 |
16 |
Р |
0,6 |
0,4 |
М[X2]=4×0,6+16×0,4=8,8; DX=8,8-(2,8)2=0,96.
Задача 3.
Согласно таблицам смертности, вероятность того, что 25-летний человек проживет еще один год равна 0,992; а вероятность того, что он умрет в течение года равна 0,008. Страховая компания предлагает застраховать жизнь на 10000 рублей. Какова должна быть величина годового взноса, чтобы подобная страховка не была для страховых органов убыточной?
Решение.
Пусть Х – случайная величина, равная выплате застрахованному лицу страховой суммы (за вычетом страхового взноса а). Тогда закон распределения случайной величины Х будет таким:
Х |
а-10000 |
а |
Р |
0,008 |
0,992 |
х1=а-10000, если застрахованный умрет и х2=а, если застрахованный проживет еще
год.
МХ=(а-10000)×0,008+а×0,992=(а-80).
Чтобы страховые органы в среднем не терпели убытка, необходимо, чтобы МХ³0, следовательно, а³80 рублей.
Задача 4
Дискретная случайная величина X может принимать только два значения x1 и x2 , причем x1 < x2 . Известна вероятность p1 = P{ X = x1} = 0,1, MX = 3,9, DX = 0,09 . Написать закон распределения дискретной случайной величины.
Решение.
Составим таблицу: в первом ряду возможные значения случайной величины, во втором – вероятности, с которыми она эти значения принимает:
Х |
x1 |
x2 |
Р |
p1 = 0,1 |
p |
|
|
2 |
Т.к. p1 + p2 = 1, то |
p2 = 1− 0,1 = 0,9 . |
|
Запишем MX :
MX = x1 Ч0,1+ x2 Ч0,9 = 3,9 . Найдем DX :
20
