Вопросы для самопроверки (знать).
Пороговый уровень:
Запишите различные виды уравнений плоскости в пространстве и поясните смысл параметров, входящих в уравнения.
Как определяется взаимное расположение плоскостей? Запишите условия параллельности и перпендикулярности плоскостей.
Как вычисляется расстояние от точки до плоскости?
Запишите различные виды уравнений прямой в пространстве и поясните смысл параметров, входящих в уравнения.
Как определить взаимное расположение прямых в пространстве?
Как вычисляется расстояние от точки до прямой в пространстве?
Как определить взаимное расположение прямой и плоскости?
Как находится точка пересечения прямой и плоскости?
Повышенный уровень:
Дайте развернутые ответы на следующие вопросы (доказательства свойств или теорем, встречающихся в данном вопросе, являются обязательными):
Расстояние между прямыми в пространстве.
Нахождение общего перпендикуляра к двум скрещивающимся прямым.
Взаимное расположение прямой и плоскости.
Взаимное расположение трёх плоскостей.
Связка плоскостей.
Пучок плоскостей.
Решение типовых задач (уметь). Лабораторная работа №3.
Вариант 1.
1.
Составить уравнение плоскости, проходящей
через точки
и
и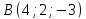 перпендикулярной плоскости
.
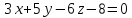2.
Дана пирамида
.
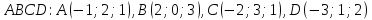Найти угол между гранями
и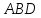
.
3.
Дан тетраэдр
с вершинами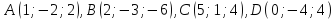
.
Написать уравнение плоскости
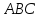и найти уравнение высоты, проведенной
из вершины
.
4.
Составить каноническое уравнение
прямой, которая является линией
пересечения двух плоскостей:
.
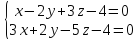5.
Найти проекцию точки
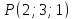на прямую
.
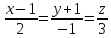6. Вычислить кратчайшее расстояние между двумя прямым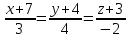и:
и
.
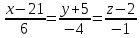7.
Найти угол между прямой
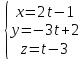и плоскостью
.
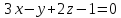Вариант 2.
1.
Составить уравнение плоскости,
параллельной оси
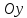и проходящей через точки
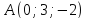и
.
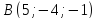2.
Дана пирамида
.
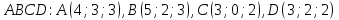Найти угол между гранями
и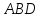
.
3.
Даны 3 точки:
.
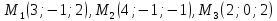Составить уравнение плоскости
,
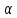проходящей через эти точки.Записать каноническое уравнение прямой, перпендикулярной плоскости α и проходящей через точку
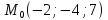.Найти точку пересечения найденной прямой и плоскости α.
4.
Составить каноническое уравнение
прямой, которая является линией
пересечения двух плоскостей:
.
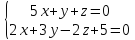5.
Найти проекцию точки
на прямую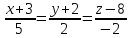
.
6.
Вычислить кратчайшее расстояние между
двумя прямыми:
.
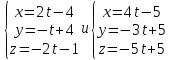7.
Найти угол между прямой
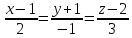и плоскостью
.
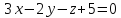Вариант 3.
1.
Составить уравнение плоскости,
параллельной оси
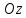и проходящей через точки
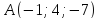и
.
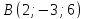2.
Дана пирамида
.
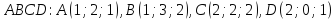Найти угол между гранями
и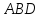
.
3.
Дан тетраэдр
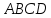с вершинами
.
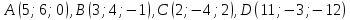Написать уравнение плоскости
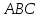и найти уравнение высоты, проведенной
из вершины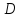
.
4.
Составить каноническое уравнение
прямой, которая является линией
пересечения двух плоскостей:
.
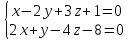5.
Найти проекцию точки
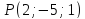на прямую, проходящую через точки
.
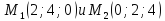6. Вычислить кратчайшее расстояние между двумя прямым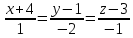и:
и
.
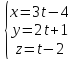7.
Найти угол между прямой
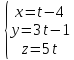и плоскостью
.
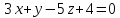Вариант 4.
1.
Составить уравнение плоскости, проходящей
через точки
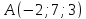и
и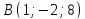 перпендикулярной плоскости
.
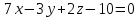2.
Дана пирамида
.
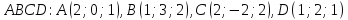Найти угол между граням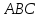и
и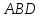
.
3.
Дан тетраэдр
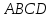с вершинами
.
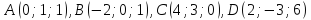Написать уравнение плоскости
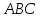и найти уравнение высоты, проведенной
из вершины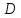
.
4.
Составить параметрическое уравнение
прямой, которая является линией
пересечения двух плоскостей:
.
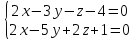5.
Найти расстояние от точки
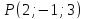до прямой
.
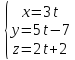6. Вычислить кратчайшее расстояние между двумя прямым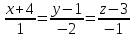и:
и
.
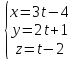7.
Найти угол между прямой
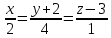и плоскостью
.
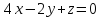Вариант 5.
1.
Составить уравнение плоскости, проходящей
через точки
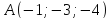и
и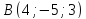 перпендикулярной плоскости
.
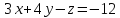2.
Дана пирамида
.
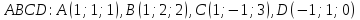Найти угол между граням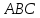и
и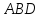
.
3.
Дан тетраэдр
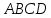с вершинами
.
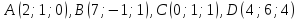Написать уравнение плоскости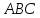
и найти уравнение высоты, проведенной
из вершины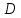
.
4.
Составить параметрическое уравнение
прямой, которая является линией
пересечения двух плоскостей:
.
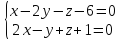5.
Найти расстояние от точки
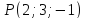до прямой
.
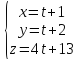6. Вычислить кратчайшее расстояние между двумя прямым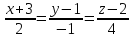и:
и
.
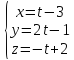7.Найти
угол между прямой
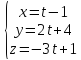и плоскостью
.
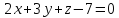Вариант 6.
1.
Составить уравнение плоскости, проходящей
через точку
,
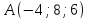параллельной вектору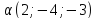
и перпендикулярной плоскости
.
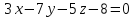2.
Дана пирамида
.
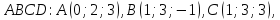
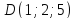Найти угол между гранями
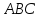и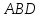
.
3.
Дан тетраэдр
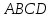с вершинами
.
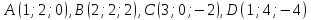Написать уравнение плоскости
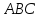и найти уравнение высоты, проведенной
из вершины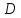
.
4.
Доказать перпендикулярность прямых:
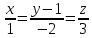и
.
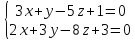5.
Найти расстояние от точки
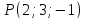до прямой
.
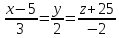6. Вычислить кратчайшее расстояние между двумя прямым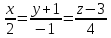и:
и
.
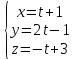7.
При каком значении m
прямая
параллельна плоскости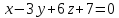
?
Вариант 7.
1.
Составить уравнение плоскости, проходящей
через точки
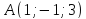и
и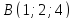 перпендикулярной плоскости
.
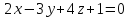2.
Дана пирамида
.
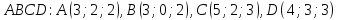Найти угол между граням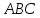и
и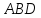
.
3.
Дан тетраэдр
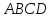с вершинами
.
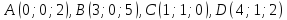Написать уравнение высоты, проведенной
из вершины
и найти ее основание.
4.
Доказать параллельность прямых:
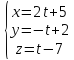и
.
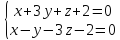5.
Найти расстояние от точки
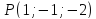до прямой
.
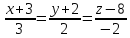6. Вычислить кратчайшее расстояние между двумя прямым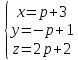и:
и
.
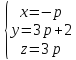7.
При каких значениях
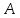и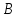
плоскость
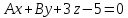перпендикулярна прямой
.
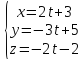Вариант 8.
1.
Составить уравнение плоскости, проходящей
через точк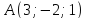и
и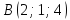
параллельно оси
.
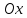2.
Дана пирамида
.
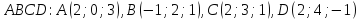Найти угол между гранями
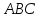и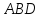
.
3.
Дан тетраэдр
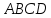с вершинами
.
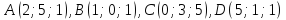Написать уравнение плоскости
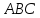и найти уравнение высоты, проведенной
из вершины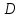
.
4.
Найти каноническое уравнение прямой
.
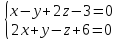5.
Найти проекцию прямой
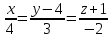на плоскость
.
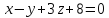6.
Вычислить кратчайшее расстояние между
двумя прямыми:
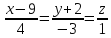и
.
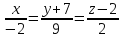7.
При каких значениях
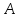и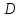
прямая
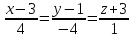лежит в плоскости
.
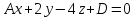Пороговый уровень:
Достаточно правильно решить 70 % задач лабораторной работы №3.
Повышенный уровень:
Необходимо правильно решить все задачи лабораторной работы №3.
Кейс-задание предполагает готовность к педагогической деятельности, владение компьютерными технологиями и демонстрирует возможность использования идей аналитической геометрии для решения ряда стереометрических задач и заключается в следующем:
Используя компьютерные технологии проиллюстрировать решение стереометрических задач (нахождение расстояний между скрещивающимися прямыми, от точки до прямой, от точки до плоскости; вычисление угла между плоскостями, между скрещивающимися прямыми и др.).
При этом для порогового уровня достаточно иллюстрации 5 задач и в качестве примера может рассматриваться только куб.
Для продвинутого уровня необходима иллюстрация хотя бы 10 задач и фигуры в условиях задач должны быть разнообразны.