
- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
Вопросы для самопроверки (знать).
Пороговый уровень:
Прямая линия на плоскости, её общее уравнение
Понятие нормального и направляющего векторов прямой на плоскости, углового коэффициента.
Различные виды уравнений прямой и геометрический смысл параметров уравнения.
Угол между прямыми. Условия параллельности и перпендикулярности прямых на плоскости в случае различных видов уравнений прямых.
Формула расстояния от точки до прямой на плоскости?
Повышенный уровень:
Дайте развернутые ответы на следующие вопросы (доказательства свойств, встречающихся в данном вопросе являются обязательными):
Линия как геометрическое место точек, обладающих каким-либо определенным свойством. Уравнение линии как связь между координатами произвольной ее точки, выраженная аналитически.
Прямая линия. Общее уравнение прямой. Взаимно однозначное соответствие между уравнением первой степени с двумя переменными
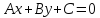 и прямой линией.
и прямой линией.Различные виды уравнений прямой и их выводы. Записать различные виды уравнений прямой по одному из заданных.
Пучок прямых.
Отклонение точки от прямой. Применение в решении задач.
Решение типовых задач (уметь). Лабораторная работа №2.
Вариант 1
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
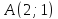 и
и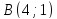 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Дана прямая
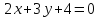 .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку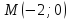 :
а) параллельно данной прямой; б)
перпендикулярно данной прямой.
:
а) параллельно данной прямой; б)
перпендикулярно данной прямой.Найти точку пересечения двух прямых
 и
и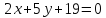 и угол между ними.
и угол между ними.При каких
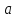 и
и прямые
прямые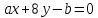 и
и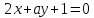 :
:
1) параллельны; 2) совпадают; 3) перпендикулярны?
Составить уравнение прямой, если точка
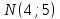 служит основанием перпендикуляра,
опущенного из начала координат на
эту прямую.
служит основанием перпендикуляра,
опущенного из начала координат на
эту прямую.Докажите, что данные прямые параллельны и найдите расстояние между ними:
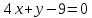 и
и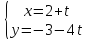 .
.
Дано уравнение пучка прямых
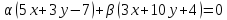 .
Найти все значенияа,
при которых прямая
.
Найти все значенияа,
при которых прямая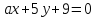 не принадлежит данному пучку.
не принадлежит данному пучку.Диагональ квадрата расположена на прямой
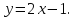 Одна из его вершин находится в точке
Одна из его вершин находится в точке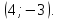 Составить уравнения его сторон и второй
диагонали.
Составить уравнения его сторон и второй
диагонали.
Вариант 2
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
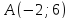 и
и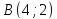 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Составьте общее уравнение прямой, проходящей через точку
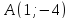 :
а) перпендикулярно; б) параллельно
прямой
:
а) перпендикулярно; б) параллельно
прямой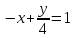 .
.Докажите, что прямые
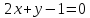 и
и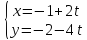 параллельные и найдите расстояние
между ними.
параллельные и найдите расстояние
между ними.При каких
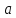 и
и прямые
прямые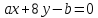 и
и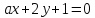 :
:
1) параллельны; 2) совпадают; 3) перпендикулярны?
Найти проекцию точки
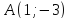 на прямую
на прямую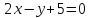 .
.Составить уравнение биссектрисы угла между прямыми
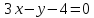 и
и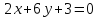 ,
в котором лежит начало координат.
,
в котором лежит начало координат.Найти уравнение прямой, принадлежащей пучку
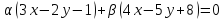 и проходящей через середину отрезка
прямой
и проходящей через середину отрезка
прямой ,
заключенного между прямыми
,
заключенного между прямыми и
и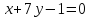 .
.Центр симметрии квадрата находится в точке
 уравнение одной из его сторон
уравнение одной из его сторон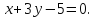 Составить уравнения трех других сторон
квадрата.
Составить уравнения трех других сторон
квадрата.
Вариант 3
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
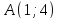 и
и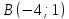 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Найдите параметрические уравнения прямой, проходящей через вершину
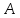 треугольника
треугольника :
а) параллельно; б) перпендикулярно
стороне
:
а) параллельно; б) перпендикулярно
стороне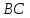 ,
если
,
если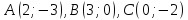 .
.Написать уравнение прямой, проходящей через точку
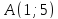 на расстоянии пять единиц от начала
координат.
на расстоянии пять единиц от начала
координат.При каких
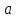 и
и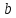 прямые
прямые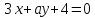 и
и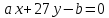 :
:
1) параллельны; 2) совпадают; 3) перпендикулярны?
Найти координаты точки
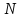 ,
симметричной точке
,
симметричной точке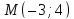 относительно прямой
относительно прямой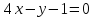 .
.Составить уравнение биссектрисы угла между прямыми
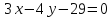 и
и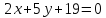 ,
в котором лежит начало координат.
,
в котором лежит начало координат.Из пучка прямых
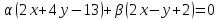 выберите прямую, проходящую через
точку
выберите прямую, проходящую через
точку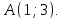
Известны координаты точек
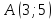 и
и На прямой
На прямой найти такую точку
найти такую точку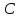 ,
что площадь треугольника
,
что площадь треугольника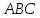 равна
равна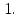
Вариант 4
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
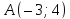 и
и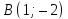 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Найдите уравнение прямой в отрезках, проходящей через вершину
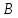 треугольника
треугольника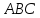 :
а) параллельно; б) перпендикулярно
стороне
:
а) параллельно; б) перпендикулярно
стороне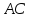 ,
если
,
если
Найти расстояние между параллельными прямыми:
 и
и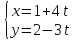 .
.При каких
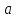 и
и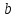 прямые
прямые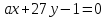 и
и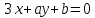 :
:
1) параллельны; 2) совпадают; 3) перпендикулярны?
Даны уравнения сторон треугольника
 .
Найти уравнение перпендикуляра,
опущенного из вершины
.
Найти уравнение перпендикуляра,
опущенного из вершины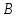 на медиану, проведенную из вершины
на медиану, проведенную из вершины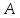 .
.Определить высоту
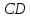 в треугольнике
в треугольнике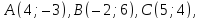 вычислив расстояние от точки
вычислив расстояние от точки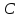 до прямой
до прямой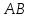 .
.Из пучка прямых
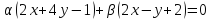 выберите прямую параллельную прямой
выберите прямую параллельную прямой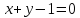 .
.Составьте уравнения сторон треугольника, если его вершина
 ,
а биссектриса
,
а биссектриса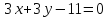 и медиана
и медиана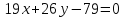 ,
проведены из другой его вершины.
,
проведены из другой его вершины.
Вариант 5
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
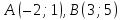 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Составьте общее уравнение прямой, проходящей через точку
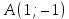 а)
перпендикулярно; б) параллельно прямой
а)
перпендикулярно; б) параллельно прямой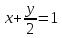 .
.Найти расстояние между прямыми:
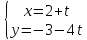 и
и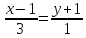 .
.При каких
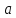 и
и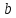 прямые
прямые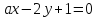 и
и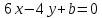 :
:
1) имеют одну общую точку; 2) параллельны; 3) совпадают; 4) перпендикулярны?
Даны две противоположные вершины квадрата
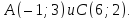 Найти уравнения его сторон.
Найти уравнения его сторон.Определить высоту
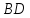 в треугольнике
в треугольнике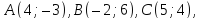 вычислив расстояние от точки
вычислив расстояние от точки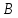 до прямой
до прямой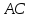 .
.Из пучка прямых
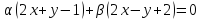 выберите прямую перпендикулярную
прямой
выберите прямую перпендикулярную
прямой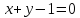 .
.Составить уравнения сторон ромба, зная две противоположные вершины
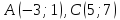 и площадь
и площадь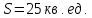
Вариант 6
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
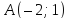 и
и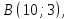 ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Найдите параметрические уравнения прямой, проходящей через вершину
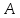 треугольника
треугольника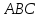 и а) параллельно; б) перпендикулярно
стороне
и а) параллельно; б) перпендикулярно
стороне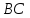 ,
если
,
если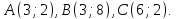
Точка
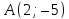 является вершиной квадрата, одна из
сторон которого лежит на прямой
является вершиной квадрата, одна из
сторон которого лежит на прямой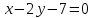 .
Найти площадь этого квадрата.
.
Найти площадь этого квадрата.При каких
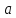 и
и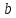 прямые
прямые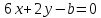 и
и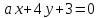 :
:
имеют одну общую точку;
параллельны;
совпадают;
перпендикулярны?
Найти уравнение прямой, проходящей через точку с координатами
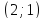 под углом
под углом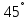 к прямой
к прямой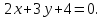
Найти точку
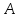 ,
симметричную точке
,
симметричную точке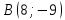 относительно
прямой
относительно
прямой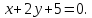
Докажите, что прямая
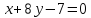 принадлежит пучку
принадлежит пучку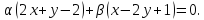
Дана вершина равнобедренного треугольника
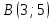 ,
уравнение его основания
,
уравнение его основания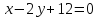 и площадь
и площадь Составить уравнения его боковых сторон.
Составить уравнения его боковых сторон.
Вариант 7
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
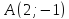 и
и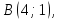 ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Составьте общее уравнение прямой, проходящей через точку
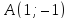 :
а) перпендикулярно; б) параллельно
биссектрисе второго и четвертого
координатных углов.
:
а) перпендикулярно; б) параллельно
биссектрисе второго и четвертого
координатных углов.Составить уравнение прямой, симметричной прямой
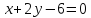 относительно точки
относительно точки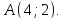
При каких
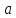 и
и прямые
прямые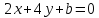 и
и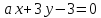 :
:
имеют одну общую точку;
параллельны;
совпадают;
перпендикулярны?
Составить уравнения сторон треугольника, зная координаты одной из его вершин
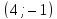 и уравнения двух биссектрис:
и уравнения двух биссектрис: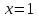 и
и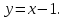
Даны уравнения оснований трапеции:
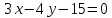 ,
,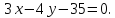 Найти высоту трапеции.
Найти высоту трапеции.Из пучка прямых
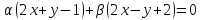 выберите две взаимно перпендикулярных
прямых.
выберите две взаимно перпендикулярных
прямых.Составьте уравнения сторон треугольника, если известны координаты двух его вершин
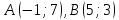 и точка пересечения медиан
и точка пересечения медиан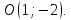
Вариант 8
Напишите все виды уравнений (канонические, параметрические, общее, в отрезках, с угловым коэффициентом) для прямой, проходящей через точки
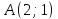 и
и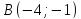 ,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.
,
ее угловой коэффициент, нормальный и
направляющий векторы, точки пересечения
с координатными осями. Сделайте чертеж.Составьте общее уравнение прямой, проходящей через точку
 а) перпендикулярно; б) параллельно
биссектрисе первого и третьего
координатных углов.
а) перпендикулярно; б) параллельно
биссектрисе первого и третьего
координатных углов.Даны 3 параллельные прямые
 .
Установить, что первая из них лежит
между двумя другими, и вычислить
отношение, в котором она делит расстояние
между ними.
.
Установить, что первая из них лежит
между двумя другими, и вычислить
отношение, в котором она делит расстояние
между ними.При каких
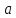 и
и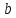 прямые
прямые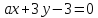 и
и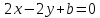 :
:
имеют одну общую точку;
параллельны;
совпадают;
перпендикулярны?
Составить уравнение прямой, проходящей через начало координат, зная, что длина её отрезка, заключённого между прямыми
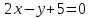 и
и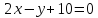 ,
равна
,
равна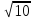 .
.Определить высоту
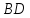 в треугольнике
в треугольнике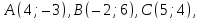 вычислив расстояние от точки
вычислив расстояние от точки до прямой
до прямой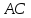 .
.При каком значении
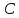 прямая
прямая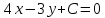 принадлежит пучку
принадлежит пучку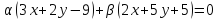 .
.Даны уравнения двух медиан треугольника
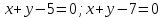 и уравнение одной из его сторон
и уравнение одной из его сторон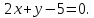 Составить уравнения двух других сторон
треугольника и найти его вершины.
Составить уравнения двух других сторон
треугольника и найти его вершины.
Пороговый уровень:
Достаточно правильно решить 70 % задач лабораторной работы №2.
Повышенный уровень:
Необходимо правильно решить все задачи лабораторной работы №2.
Кейс-задание диагностирует готовность к педагогической деятельности и заключается в следующем:
На основе предложенных в учебно-методическом пособии типовых задач составить систему тестовых заданий, позволяющих оценить когнитивную составляющую формируемых компетенций.
При этом для порогового уровня достаточно демонстрационного варианта теста.
Для продвинутого уровня необходимо создание хотя бы 5 вариантов с выделением уровня сформированности когнитивной составляющей формируемых компетенций.
