
- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
Вопросы для самопроверки (знать).
Пороговый уровень:
Как выполняются линейные операции над векторами? Каковы свойства этих операций?
Какие вектора называются линейно зависимыми, а какие линейно независимыми?
Что такое базис? Какие векторы образуют базис на плоскости и в пространстве?
Какой базис называют ортонормированным?
Что такое координаты вектора?
Что называется скалярным произведением векторов? Каковы его свойства? Для решения каких задач и как оно может быть использовано?
Что называется векторным произведением векторов? Каковы его свойства? Для решения каких задач и как оно может быть использовано?
Что называется смешанным произведением векторов? Каковы его свойства? Для решения каких задач и как оно может быть использовано?
Запишите в векторной и координатной формах условия коллинеарности, ортогональности и компланарности векторов.
Повышенный уровень:
Докажите свойства скалярного произведения векторов.
Докажите свойства векторного произведения векторов.
Докажите свойства смешанного произведения векторов.
Докажите выражение скалярного, векторного и смешанного произведения векторов через их координаты, заданных в ортонормированном базисе.
Для решения каких задач школьного курса геометрии и как используются свойства векторов?
Приведите примеры использования векторов в других областях науки, например в физике.
Решение типовых задач (уметь). Лабораторная работа №1.
Вариант 1.
Даны координаты вершин пирамиды
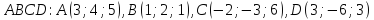 .
.
Задание:
найти координаты векторов

найти угол между векторами
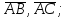
найти проекцию
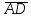 на вектор
на вектор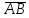 ;
;найти площадь грани ABD;
найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
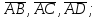
найти орт вектора
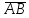 ;
;найти координаты центра тяжести треугольника
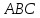 .
.
Дано:
 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины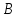 треугольника
треугольника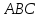 .
.Доказать, что векторы
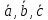 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора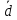 в этом базисе:
в этом базисе: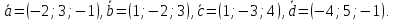
Даны векторы
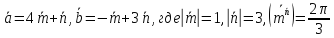 .
Найти проекцию
.
Найти проекцию
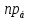 (
( ).
).Найти
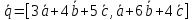 ,
если
,
если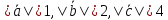 ,
причем
,
причем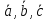 – взаимно перпендикулярны и образуют
правую тройку.
– взаимно перпендикулярны и образуют
правую тройку.Найти площадь параллелограмма, построенного на векторах
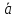 и
и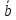 ,
если
,
если
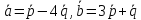 ,
,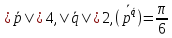 .
.Вектор
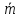 ,
перпендикулярный к векторам
,
перпендикулярный к векторам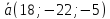 и
и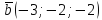 ,
образует острый угол с осьюOy.
Зная, что
,
образует острый угол с осьюOy.
Зная, что
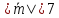 ,
найти его координаты.
,
найти его координаты.
Вариант 2.
Даны координаты вершин пирамиды
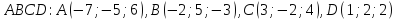 .
.
Задание:
найти координаты векторов
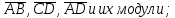
найти угол между векторами
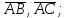
найти проекцию
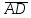 на вектор
на вектор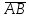 ;
;найти площадь грани
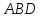 ;
;найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
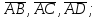
найти орт вектора
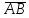 ;
;найти координаты центра тяжести треугольника
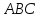 .
.
Дано:
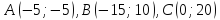 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины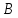 треугольника
треугольника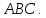
Доказать, что векторы
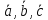 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора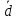 в этом базисе:
в этом базисе: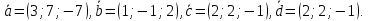
Даны векторы
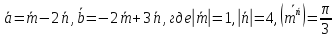 .
Найти проекцию
.
Найти проекцию
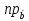 (
(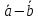 ).
).Найти
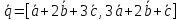 ,
если
,
если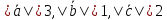 ,
причем
,
причем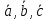 – взаимно перпендикулярны и образуют
правую тройку.
– взаимно перпендикулярны и образуют
правую тройку.Найти площадь параллелограмма, построенного на векторах
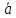 и
и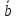 ,
если
,
если
 ,
,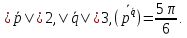
Вектор
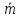 ,
перпендикулярный к осиOz
и к вектору
,
перпендикулярный к осиOz
и к вектору
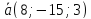 ,
образует острый угол с осьюOx.
Зная, что
,
образует острый угол с осьюOx.
Зная, что
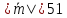 ,
найти его координаты.
,
найти его координаты.
Вариант 3.
Даны координаты вершин пирамиды
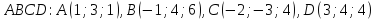 .
.
Задание:
найти координаты векторов
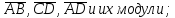
найти угол между векторами
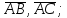
найти проекцию
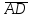 на вектор
на вектор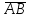 ;
;найти площадь грани
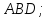
найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
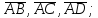
найти орт вектора
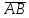 ;
;найти координаты центра тяжести треугольника
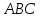 .
.
Дано:
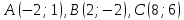 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины треугольника
треугольника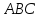
Доказать, что векторы
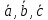 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора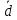 в этом базисе:
в этом базисе: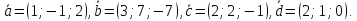
Даны векторы
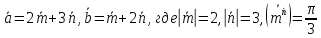 .
Найти проекцию
.
Найти проекцию
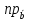 (2
(2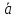 +
+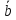 ).
).Найти
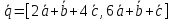 ,
если
,
если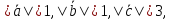 причем
причем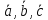 – взаимно перпендикулярны и образуют
правую тройку.
– взаимно перпендикулярны и образуют
правую тройку.Найти угол между векторами
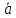 и
и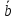 ,
если
,
если
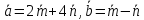 ,
,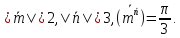
Найти вектор
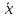 ,
зная, что он перпендикулярен к векторам
,
зная, что он перпендикулярен к векторам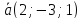 и
и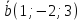 и удовлетворяет условию
и удовлетворяет условию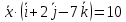 .
.
Вариант 4.
Даны координаты вершин пирамиды
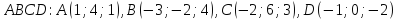 .
.
Задание:
найти координаты векторов
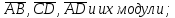
найти угол между векторами
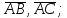
найти проекцию
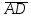 на вектор
на вектор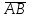 ;
;найти площадь грани
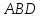 ;
;найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
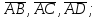
найти орт вектора
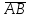 ;
;найти координаты центра тяжести треугольника
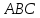 .
.
Дано:
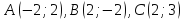 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины треугольника
треугольника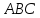 .
.Доказать, что векторы
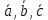 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора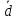 в этом базисе:
в этом базисе: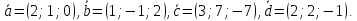
Даны векторы
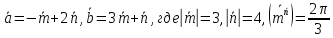 .
Найти проекцию
.
Найти проекцию
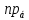 (
(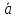 +2
+2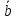 ).
).Найти
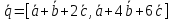 ,
если
,
если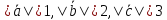 ,
причем
,
причем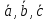 – взаимно перпендикулярны и образуют
правую тройку.
– взаимно перпендикулярны и образуют
правую тройку.Найти угол между векторами
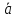 и
и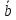 ,
если
,
если
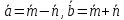 ,
,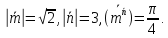
Даны координаты вершин пирамиды
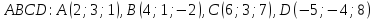 .
Найти длину его высоты, опущенной из
вершины
.
Найти длину его высоты, опущенной из
вершины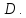
Вариант 5.
Даны координаты вершин пирамиды
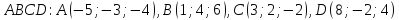 .
.
Задание:
найти координаты векторов
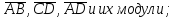
найти угол между векторами
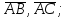
найти проекцию
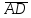 на вектор
на вектор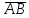 ;
;найти площадь грани
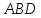 ;
;найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
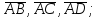
найти орт вектора
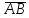 ;
;найти координаты центра тяжести треугольника
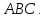
Дано:
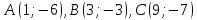 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины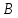 треугольника
треугольника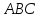
Доказать, что векторы
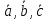 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора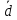 в этом базисе:
в этом базисе: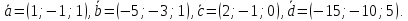
Даны векторы
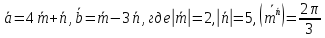 .
Найти проекцию
.
Найти проекцию
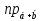 (
(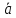 -3
-3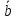 ).
).Найти объем параллелепипеда, построенного на векторах
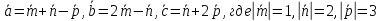 ,
причем
,
причем
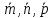 –
взаимно перпендикулярны и образуют
правую тройку.
–
взаимно перпендикулярны и образуют
правую тройку.Найти площадь параллелограмма, построенного на векторах
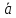 и
и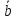 ,
если
,
если
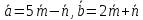 ,
,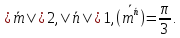
Объем тетраэдра
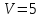 ,
координаты вершин находятся в точках
,
координаты вершин находятся в точках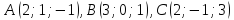 .
Найти координаты четвертой вершиныD,
если известно, что она лежит на оси Oy.
.
Найти координаты четвертой вершиныD,
если известно, что она лежит на оси Oy.
Вариант 6.
Даны координаты вершин пирамиды
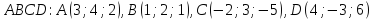 .
.
Задание:
найти координаты векторов
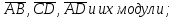
найти угол между векторами
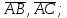
найти проекцию
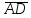 на вектор
на вектор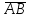 ;
;найти площадь грани
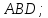
найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
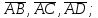
найти орт вектора
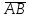 ;
;найти координаты центра тяжести треугольника
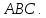
Дано:
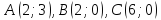 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины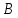 треугольника
треугольника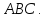
Доказать, что векторы
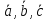 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора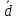 в этом базисе:
в этом базисе: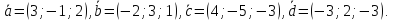
Даны векторы
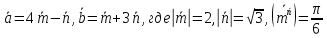 .
Найти проекцию
.
Найти проекцию
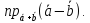
Найти объем параллелепипеда, построенного на векторах
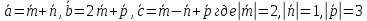 ,
причем
,
причем
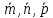 – взаимно перпендикулярны и образуют
правую тройку.
– взаимно перпендикулярны и образуют
правую тройку.Найти угол между векторами
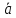 и
и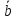 ,
если
,
если
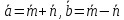 ,
,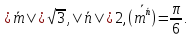
Вектор
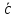 перпендикулярен к векторам
перпендикулярен к векторам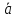 и
и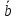 ,
угол между
,
угол между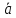 и
и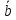 равен
равен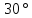 .
Зная, что
.
Зная, что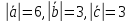 ,
вычислить
,
вычислить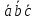 .
.
Вариант 7.
Даны координаты вершин пирамиды
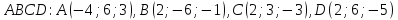 .
.
Задание:
найти координаты векторов
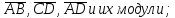
найти угол между векторами
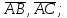
найти проекцию
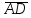 на вектор
на вектор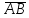 ;
;найти площадь грани
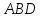 ;
;найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
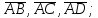
найти орт вектора
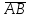 ;
;найти координаты центра тяжести треугольника
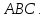
Дано:
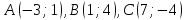 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины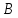 треугольника
треугольника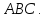
Доказать, что векторы
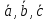 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора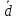 в этом базисе:
в этом базисе: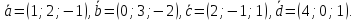
Даны векторы
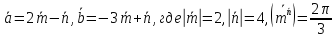 .
Найти проекцию
.
Найти проекцию
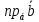 .
.Найти
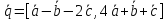 ,
если
,
если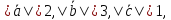 причем
причем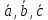 – взаимно перпендикулярны и образуют
правую тройку
– взаимно перпендикулярны и образуют
правую тройкуНайти площадь параллелограмма, построенного на векторах
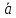 и
и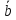 ,
если
,
если
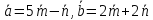 ,
,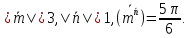
Найти вектор
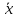 ,
зная,
что он перпендикулярен к векторам
,
зная,
что он перпендикулярен к векторам
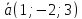 и
и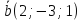 и удовлетворяет условию
и удовлетворяет условию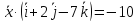 .
.
Вариант 8.
Даны координаты вершин пирамиды
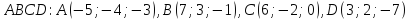 .
.
Задание:
найти координаты векторов
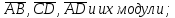
найти угол между векторами
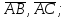
найти проекцию
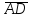 на вектор
на вектор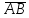 ;
;найти площадь грани
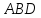 ;
;найти объем пирамиды;
определить, какой тройкой (левой или правой) являются векторы
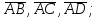
найти орт вектора
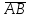 ;
;найти координаты центра тяжести треугольника
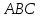 .
.
Дано:
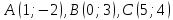 .
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины
.
Найти координаты высоты, биссектрисы
и медианы, проведенных из вершины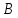 треугольника
треугольника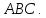
Доказать, что векторы
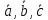 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора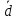 в этом базисе:
в этом базисе: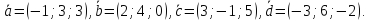
Даны векторы
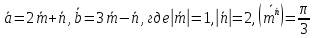 .
Найти проекцию
.
Найти проекцию
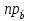 (
(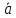 ).
).Найти объем параллелепипеда, построенного на векторах
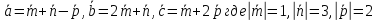 ,
причем
,
причем
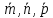 –
взаимно перпендикулярны и образуют
правую тройку.
–
взаимно перпендикулярны и образуют
правую тройку.Найти площадь параллелограмма, построенного на векторах
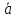 и
и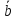 ,
если
,
если
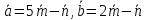 ,
,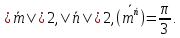
Найти вектор
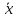 ,
зная, что он перпендикулярен к векторам
,
зная, что он перпендикулярен к векторам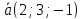 и
и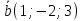 и удовлетворяет условию
и удовлетворяет условию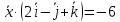 .
.
Пороговый уровень:
Достаточно правильно решить 70 % задач лабораторной работы №1.
Повышенный уровень:
Необходимо правильно решить все задачи лабораторной работы №1.
Кейс-задание диагностирует готовность к педагогической деятельности, а так же владение информационными технологиями и заключается в следующем:
Используя любой математический пакет и учебник по стереометрии для 10-11 классов создать презентации всех уроков по теме «Векторы».
При этом для достижения порогового уровня достаточно использование одного пакета и элементов презентаций на уроках по теме «Векторы».
Для продвинутого уровня необходим анализ возможностей использования компьютерных технологий в процессе изучения темы «Векторы» и создание электронного образовательного ресурса по данной теме.
