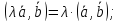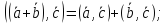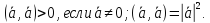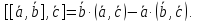- •Аналитическая геометрия
- •§1 Векторы………………………………………………………………..8
- •§1 Векторы.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №1.
- •§2 Прямая на плоскости.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №2.
- •§3 Прямая и плоскость в пространстве.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №3.
- •§4 Кривые 2-го порядка.
- •Вопросы для самопроверки (знать).
- •Решение типовых задач (уметь). Лабораторная работа №4.
- •Аналитическая геометрия практикум по решению задач
- •426034, Ижевск, Университетская, д. 1, корп. 4, каб. 207
§1 Векторы.
Определение. Вектором называется направленный отрезок. Координатами вектора называются проекции этого вектора на координатные оси.
Пусть
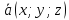 – произвольный вектор и известно, что
он образует с осями координат
– произвольный вектор и известно, что
он образует с осями координат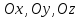 углы
углы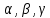 соответственно. Тогда числа
соответственно. Тогда числа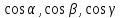 называютсянаправляющими
косинусами вектора.
Известно равенство:
называютсянаправляющими
косинусами вектора.
Известно равенство:
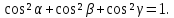
Определение.
Скалярным
произведением
двух векторов называется число, равное
произведению длин этих векторов на
косинус угла между ними:
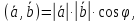 где
где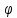 –
угол между векторами
–
угол между векторами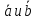 .
.
Свойства скалярного произведения:
Теорема.
Если векторы
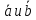 заданы декартовыми прямоугольными
координатами, то:
заданы декартовыми прямоугольными
координатами, то: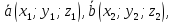 то
то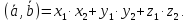
Из
теоремы и свойства (4) следует, что
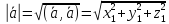 .
.
Определение.
Проекцией
вектора
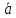 на вектор
на вектор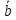 называется число:
называется число: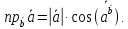
Определение.
Ортом
вектора
 называется вектор
называется вектор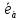 единичной длины, одинаково с ним
направленный.
единичной длины, одинаково с ним
направленный.
Применение скалярного произведения векторов:
Нахождение угла между векторами
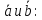
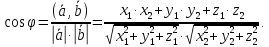
Вычисление проекции вектора
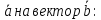
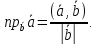
Для определения длины вектора:
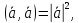 следовательно
следовательно
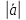 =
=
Для определения перпендикулярности векторов:
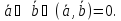
Определение.
Векторным
произведением вектора
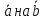 называется
вектор, обозначаемый символом [
называется
вектор, обозначаемый символом [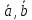 ]
и определяемый следующими тремя
условиями:
]
и определяемый следующими тремя
условиями:
Модуль вектора [
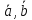 ]
равен
]
равен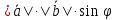 ,
гдеφ
–
угол между векторами
,
гдеφ
–
угол между векторами
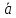 и
и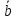 .
.Вектор [
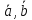 ]
перпендикулярен к каждому из векторов
]
перпендикулярен к каждому из векторов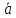 и
и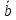 .
.Направление вектора [
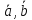 ]
соответствует «правилу правой руки».
]
соответствует «правилу правой руки».
Свойства векторного произведения:
Векторное произведение зависит от порядка сомножителей, именно:
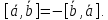
Модуль векторного произведения
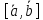 равен площадиS
параллелограмма, построенного на
векторах
равен площадиS
параллелограмма, построенного на
векторах
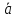 и
и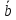 :
:
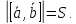
Векторное произведение может быть выражено формулой:
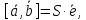 где
где
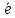 – орт векторного произведения.
– орт векторного произведения.
Векторное произведение [
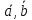 ]
обращается в нуль тогда и только тогда,
когда векторы
]
обращается в нуль тогда и только тогда,
когда векторы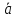 и
и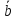 коллинеарны. В частности
коллинеарны. В частности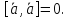
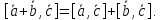
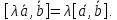
Теорема.
Если векторы
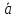 и
и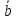 заданы декартовыми прямоугольными
координатами
заданы декартовыми прямоугольными
координатами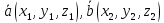 ,
то
векторное произведение вектора
,
то
векторное произведение вектора
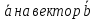 определяется формулой:
определяется формулой: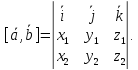
Применение векторного произведения векторов:
Для отыскания площади параллелограмма, построенного на векторах
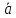 и
и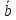 :
: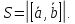
Для нахождения вектора
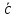 ,
перпендикулярного векторам
,
перпендикулярного векторам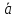 и
и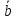 :
:
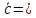 [
[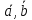 ].
].
Определение.
Если
вектор
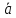 умножается векторно на вектор
умножается векторно на вектор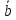 ,
и вектор [
,
и вектор [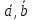 ]
также векторно умножается на вектор
]
также векторно умножается на вектор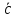 ,
то мы получаем вектор [[
,
то мы получаем вектор [[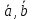 ]
]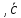 ],
который называетсядвойным
векторным произведением.
],
который называетсядвойным
векторным произведением.
Свойства:
Определение.
Смешанным
произведением
трех векторов
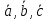 называется число, равное скалярному
произведению вектора [
называется число, равное скалярному
произведению вектора [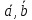 ]
на вектор
]
на вектор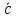 ,
т.е.
,
т.е.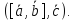
Свойство.
Имеет
место тождество:
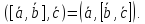
Теорема.
Смешанное произведение
 равно объему параллелепипеда, построенного
на векторах
равно объему параллелепипеда, построенного
на векторах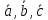 ,
взятому со знаком плюс, если тройка
,
взятому со знаком плюс, если тройка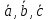 правая, и со знаком минус, если тройка
левая.
правая, и со знаком минус, если тройка
левая.
Теорема.
Векторы
 компланарны тогда и только тогда, когда
смешанное произведение
компланарны тогда и только тогда, когда
смешанное произведение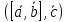 равно нулю; иначе говоря, равенство
равно нулю; иначе говоря, равенство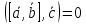 – есть необходимое и достаточноеусловие
компланарности
векторов
– есть необходимое и достаточноеусловие
компланарности
векторов
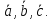
Теорема.
Если векторы
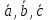 заданы декартовыми прямоугольными
координатами
заданы декартовыми прямоугольными
координатами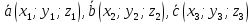 ,
то смешанное произведение
,
то смешанное произведение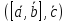 определяется формулой:
определяется формулой: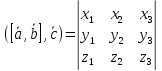 .
.
Напомним,
что система координатных осей
предполагается правой (вместе с тем
является правой и тройка векторов {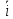 ,
,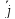 ,
,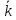 }).
}).
Применение смешанного произведения векторов:
Для отыскания объема параллелепипеда и тетраэдра, построенныхна векторах
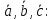
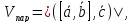
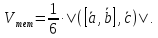
Для решения вопроса о компланарности векторов.
Для решения вопроса о линейной зависимости или независимости трех векторов.
Для решения вопроса об ориентации векторов.
Деление отрезка в данном отношении.
Пусть
на прямой заданы точки
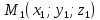 и
и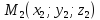 ,
а
,
а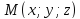 – произвольная точка прямой.
– произвольная точка прямой.
Обозначим
через
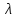 отношение
отношение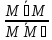 ;
будем говорить, что точка
;
будем говорить, что точка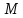 делит отрезок
делит отрезок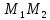 в отношении
в отношении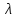 .
Известно, чтокоординаты
точки
.
Известно, чтокоординаты
точки
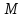 определяются по формулам:
определяются по формулам: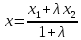 ;
;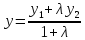 ;
;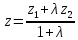 .
.
Если
точка
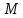 является серединой отрезка
является серединой отрезка 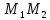 ,
то ее координаты определяются по
формулам:
,
то ее координаты определяются по
формулам:
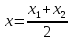 ;
;
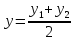 ;
;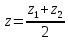 ;
;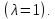
В
зависимости от положения точки
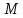 число
число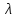 может принимать различные значения.
может принимать различные значения.
Решение типовых задач
Задача №1:
Даны
вершины треугольника
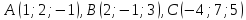 .
Вычислить координаты и длину биссектрисы
.
Вычислить координаты и длину биссектрисы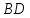 его внутреннего угла при вершине
его внутреннего угла при вершине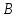 .
.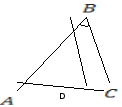
Решение:
Известно, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, т.е.
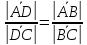 .
.Будем считать, что
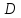 –
делящая точка отрезка АС,
–
делящая точка отрезка АС,
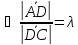 ;
;
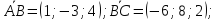 поэтому
поэтому
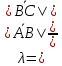

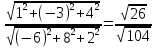
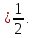 Итак,
Итак,
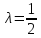 .
.
Найдем координаты т.D:
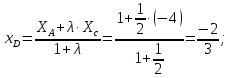
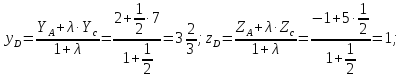
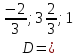 );
таким образом,
);
таким образом,
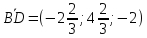 .
.
Найдем длину
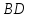 :
:
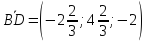 ⇒
⇒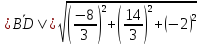
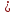
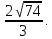
Ответ:
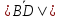
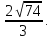
Задача №2:
Найти
направляющие косинусы биссектрисы
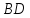 угла
угла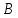 треугольника
треугольника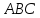 с вершинами
с вершинами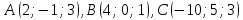 .
.
Решение:
Найдем координаты точки
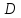 :
: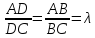 ;
;
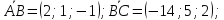
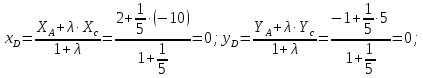
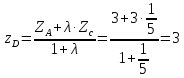 ;
таким образом,
;
таким образом,
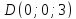 .
.
Найдем координаты
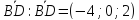 .
Пусть
.
Пусть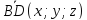 ,
тогда:
,
тогда: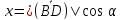 ⇒
⇒
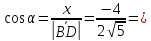
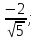
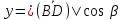 ⇒
⇒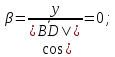
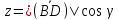 ⇒
⇒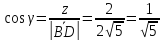 .
.
Найдем величину угла
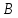 :
: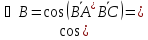
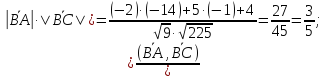
Ответ:
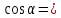
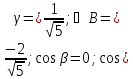 arccos
arccos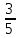 .
.
Задача №3:
Три
последовательные вершины трапеции
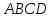 находятся в точках
находятся в точках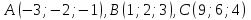 .
Найти четвертую вершину
.
Найти четвертую вершину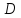 этой трапеции, зная, что длина основания
этой трапеции, зная, что длина основания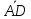 равна 15. Найти также точку
равна 15. Найти также точку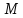 – пересечения диагоналей трапеции.
– пересечения диагоналей трапеции.
Решение: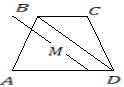
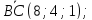
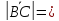 9;
9;
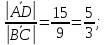 т.к.
т.к.
 и
и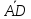 – сонаправлены⇒
– сонаправлены⇒
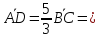 (
(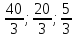 );
откуда
);
откуда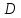 (
(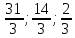 ).
).
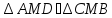 (они
подобны) ⇒
(они
подобны) ⇒
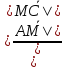
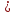
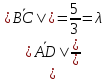 .
.
Тогда,
по формулам деления отрезка в данном
отношении,
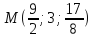 .
.
Ответ:
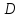 (
(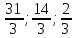 );
);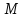 (
(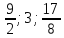 ).
).
Задача №4:
Одна
из вершин параллелепипеда
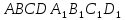 находится в точке
находится в точке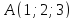 ,
а концы выходящих из нее ребер – в точках
,
а концы выходящих из нее ребер – в точках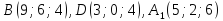 .
Найти: длину диагонали
.
Найти: длину диагонали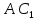 и угол
и угол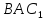 между ребром
между ребром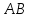 и диагональю
и диагональю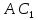 этого параллелепипеда.
этого параллелепипеда.
Решение: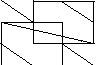
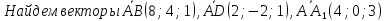 ,
,
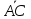 1
1
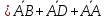 1
1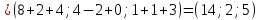 .
.
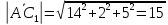 .
.
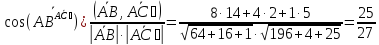 .
.
Ответ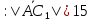 ;∠
;∠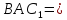 arccos
arccos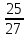 .
.
Задача №5:
Найти
проекцию вектора
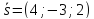 на ось, составляющую с координатными
осями равные острые углы.
на ось, составляющую с координатными
осями равные острые углы.
Решение:
Возьмём
на оси вектор
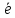 единичной
длины и найдём его координаты. Известно,
что
единичной
длины и найдём его координаты. Известно,
что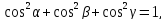 т.к.
т.к.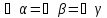 ,
то 3
,
то 3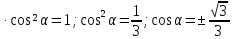 ,
берем
,
берем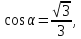 т.к. угол α острый. Итак,
т.к. угол α острый. Итак, (
(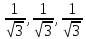 )⇒
)⇒
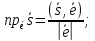
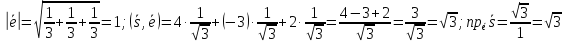 .
.
Ответ:
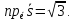
Задача №6:
Векторы
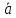 и
и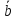 образуют угол
образуют угол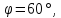 причем
причем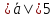 и
и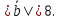
Определить
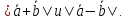
Решение:
1 способ:
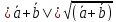 2
2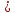
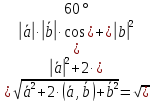
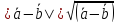 2
2
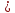
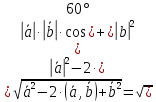
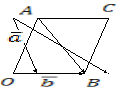
2 способ:
На
векторах
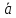 и
и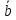 построили параллелограмм
построили параллелограмм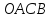 :
: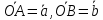 .
Очевидно, что
.
Очевидно, что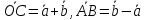 .
Из треугольника
.
Из треугольника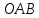 по теореме косинусов найдём
по теореме косинусов найдём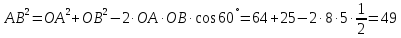 .
.
Итак,
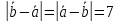 .
Из треугольника
.
Из треугольника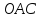 аналогично найдём
аналогично найдём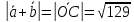 .
.
Ответ:
1)
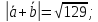 2)
2)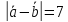 .
.
Задача №7:
Даны
векторы
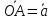 и
и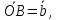 причем
причем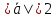 ,
,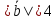 ,
угол между ними
,
угол между ними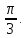 Найти угол между медианой
Найти угол между медианой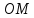 треугольника
треугольника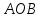 и стороной
и стороной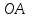 .
.
Решение:
1)
Достроим
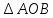 до параллелограмма
до параллелограмма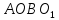 ,
для этого продолжим медиану
,
для этого продолжим медиану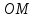 так, что
так, что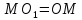 ,
,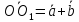 ⇒
⇒
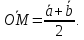
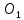
![]()
2)
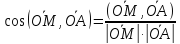 ;
;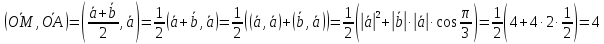 .
.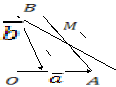
3)
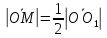 ,
,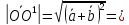
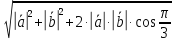
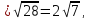
cледовательно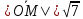 ,
,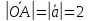 .
.
Тогда
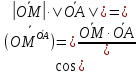
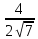
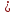
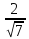 .
.
Ответ:
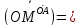 arccos
arccos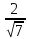 ..
..
Задача №8:
Вычислить
длину вектора
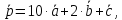 если
если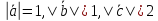 ,
,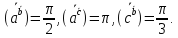
Решение:
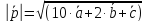 2
2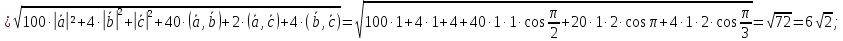
Ответ:
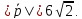
Задача №9:
Найти
угол между векторами
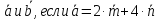 ,
,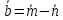 ,
,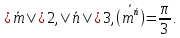
Решение:
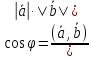 ;
;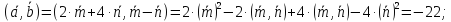
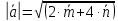 2
2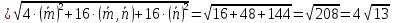 ;
;
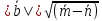 2
2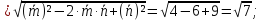
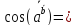
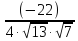
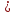
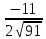 .
.
Ответ:
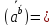 arccos(
arccos(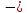
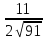 ).
).
Задача №10:
Найти
площадь параллелограмма, построенного
на векторах
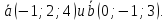
Решение:
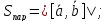
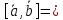

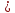
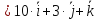
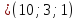 ;
;
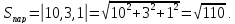
Ответ:
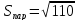 кв. ед.
кв. ед.
Задача №11:
Даны
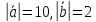 и
и .
Вычислить:
.
Вычислить: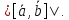
Решение:
Из определения векторного произведения следует:
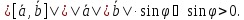
Найдем
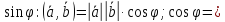
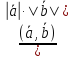 ;
;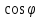
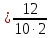 =
=
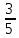 ;
;
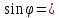
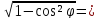
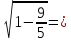
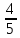 ;
поэтому
;
поэтому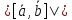 10
10 2
2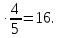
Ответ:
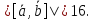
Задача №12:
Векторы
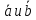 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что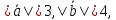 вычислить:
вычислить: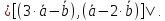
Решение:
Так
как
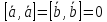 ,
то
,
то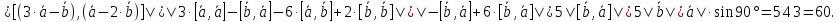
Ответ:
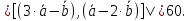
Задача №13:
Найти
площадь треугольника, построенного на
векторах
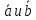 ,
если
,
если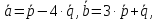
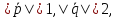 а угол между векторами
а угол между векторами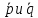 равен
равен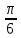 .
.
Решение:
Площадь
треугольника равна половине площади
параллелограмма построенного на векторах
 .
.
Найдём
площадь параллелограмма:
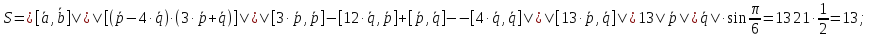
так
как
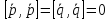 .
.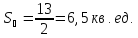
Ответ:
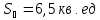 .
.
Задача №14:
Вектор
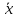 ,
перпендикулярный к векторам
,
перпендикулярный к векторам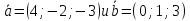 ,
образует с осью
,
образует с осью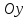 тупой угол. Зная, что
тупой угол. Зная, что ,
найти его координаты.
,
найти его координаты.
Решение:
1
способ:
Искомый вектор
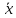 перпендикулярен
перпендикулярен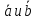 ,
поэтому мы можем его найти, как [
,
поэтому мы можем его найти, как [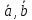 ],
но с точностью до длины.
],
но с точностью до длины.
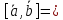
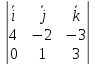
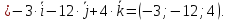
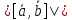
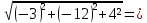
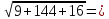
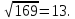
Т.к.
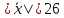 ,
а
,
а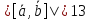 ,
мы делаем вывод, что
,
мы делаем вывод, что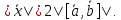 Из этого следует, что координаты вектора
Из этого следует, что координаты вектора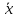 в два раза больше, чем у вектора [
в два раза больше, чем у вектора [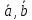 ];
];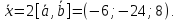
Найденный
вектор искомый, т.к. он образует с осью
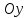 тупой угол.
тупой угол.
2
способ:
Искомый вектор
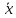 перпендикулярен к векторам
перпендикулярен к векторам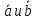 .
Значит
.
Значит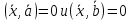 .
Также нам дано, что
.
Также нам дано, что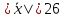 .
Обозначим координаты вектора
.
Обозначим координаты вектора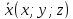 ,
тогда составим систему:
,
тогда составим систему: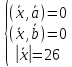 или
или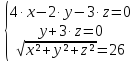 .
.
Решая
систему и зная, что вектор
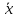 образует с осью
образует с осью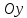 тупой угол, получаем
тупой угол, получаем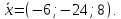
Ответ:
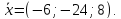
Задача №15:
Доказать,
что векторы
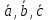 компланарны, если
компланарны, если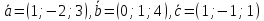 .
.
Доказательство:
([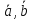 ]
]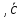 )
)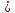
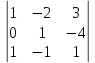
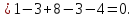
Т.к.
смешанное произведение равно нулю, то
векторы
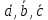 компланарны.
компланарны.
Что и требовалось доказать.
Задача №16:
Доказать,
что векторы
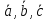 – линейно независимы, т.е. образуют
базис, если
– линейно независимы, т.е. образуют
базис, если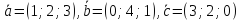 .
.
Доказательство:
([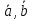 ]
]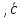 )
=
)
=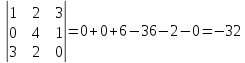 .
.
Т.к.
([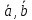 ]
]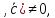 то
векторы
то
векторы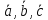 некомпланарны, а поэтому они линейно
независимы, следовательно, образуют
базис трёхмерного пространства.
некомпланарны, а поэтому они линейно
независимы, следовательно, образуют
базис трёхмерного пространства.
Что и требовалось доказать.
Задача №17:
Найти
объем параллелепипеда, построенного
на векторах
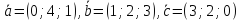 .
.
Решение:
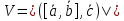
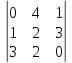
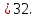
Ответ:
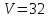 куб.ед.
куб.ед.
Задача №18:
Вычислить
объем тетраэдра, вершины которого
находятся в точках
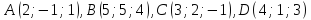 .
.
Решение:
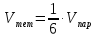 ;
([
;
([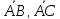 ]
]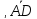 )
)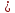
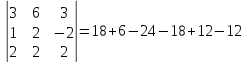
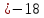 ⇒
⇒
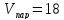 ;
;
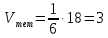 .
.
Ответ:
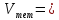
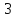 куб.
ед.
куб.
ед.
Задача №19:
Даны
вершины тетраэдра
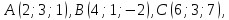
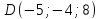 .
Найти длину его высоты, опущенной из
вершины
.
Найти длину его высоты, опущенной из
вершины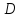 .
.
Решение:
Высота
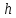 тетраэдра – это высота
тетраэдра – это высота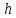 параллелепипеда, построенного на
векторах
параллелепипеда, построенного на
векторах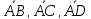 ,
поэтому найдём объём и площадь основания
параллелепипеда.
,
поэтому найдём объём и площадь основания
параллелепипеда.
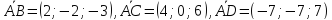 .
.
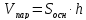 ;
следовательно
;
следовательно
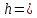
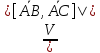 ;
;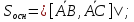
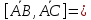
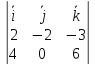
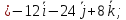
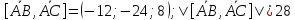 кв.
ед.;
кв.
ед.;
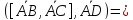

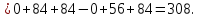
Итак,
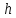 тетр
тетр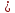
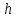 парал
парал
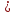
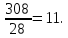
Ответ:
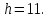
Задача №20:
Даны
три вектора
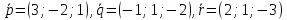 .
Найти разложение вектора
.
Найти разложение вектора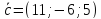 по базису
по базису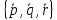 .
.
Решение:
Разложить
вектор
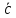 по векторам
по векторам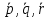 – это значит представить вектор
– это значит представить вектор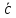 в виде линейной комбинации векторов
в виде линейной комбинации векторов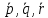 :
: ,
где
,
где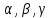 – координаты вектора
– координаты вектора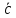 в базисе
в базисе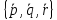 ,
то есть:
,
то есть:
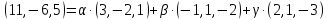 ,
,
или
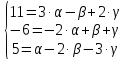 .
.
Решая
систему, находим
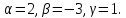
Поэтому
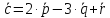 .
.
Ответ:
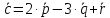 .
.
Задача №21:
Два
вектора
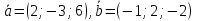 приложены к одной точке. Определить
координаты вектора
приложены к одной точке. Определить
координаты вектора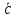 ,
направленного по биссектрисе угла между
векторами
,
направленного по биссектрисе угла между
векторами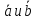 ,
при условии, что
,
при условии, что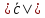 3
3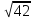 .
.
Решение:
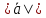
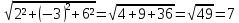 ;
;
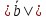
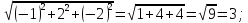
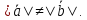
Найдем
орты векторов
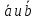 :
: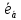
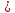
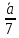
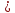 (
(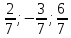 ),
),
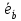
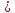
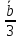
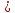 (
(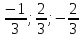 ).
).
Вектор
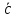 направлен по диагонали ромба, построенного
на векторах
направлен по диагонали ромба, построенного
на векторах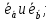
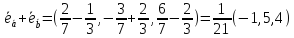 ;
;
|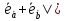
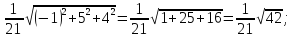
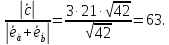
Следовательно,
длина вектора больше длины вектора в
63 раза, поэтому
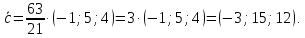
Ответ:
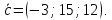
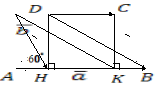
Задача №22:
В
равнобедренной трапеции
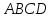 нижнее основание
нижнее основание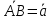 ,
боковая сторона
,
боковая сторона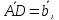 угол∠
угол∠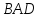 равен 60°. Выразить остальные стороны
и диагонали трапеции через векторы
равен 60°. Выразить остальные стороны
и диагонали трапеции через векторы
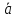 и
и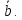
Решение:
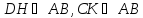 –высоты
трапеции.
–высоты
трапеции.
Тогда
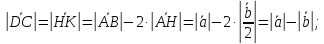
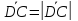

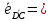
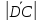

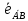
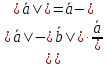
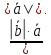
Из
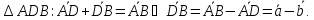
Из
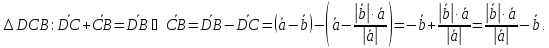
Из
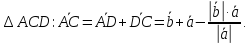
Ответ:
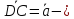
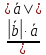 ;
;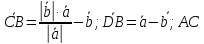 =
=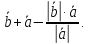
Образовательным результатом после изучения данной темы является сформированность компонент, заявленных во введении, совокупности компетенций (знать, уметь, владеть) на двух уровнях: пороговый и продвинутый. Пороговый уровень соответствует оценке «удовлетворительно», продвинутый уровень соответствует оценкам «хорошо» или «отлично» в зависимости от результатов защиты кейс-заданий.
Для самостоятельной диагностики данных компонент вам предлагаются следующие задания.