2. Уравнение нелинейной регрессии всегда дополняется показателем тесноты связи – индексом корреляции :

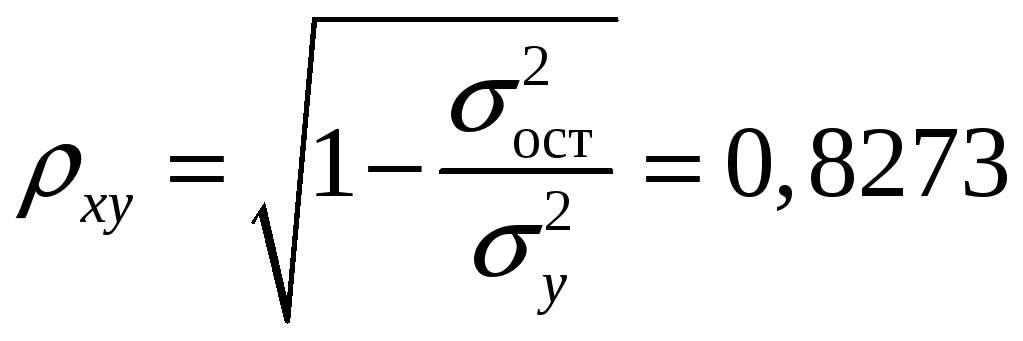
Данный индекс показывает, что связь существует, но она незначительная.

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:

,

где .

Соответственно величина характеризует долю дисперсии , вызванную влиянием остальных, не учтенных в модели, факторов.

Индекс детерминации , показывает, что уравнением регрессии объясняется 68,44% дисперсии результативного признака, а на долю прочих факторов приходится большая часть дисперсии результативного признака - 31,56%.

3. Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:

.

Так как коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора , то обычно рассчитывается средний коэффициент эластичности:

.

Для исследуемой модели . Т.е. при увеличении заработной платы на 1% от её среднего значения потребительские расходы уменьшается на -0,9938 % от своего среднего значения.

4. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

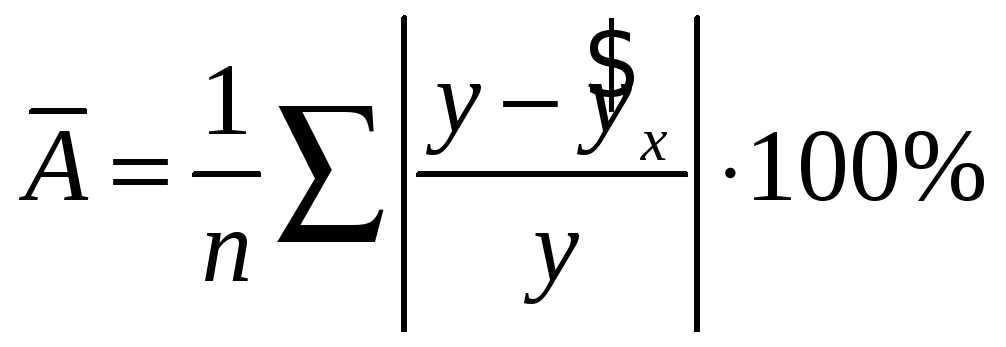. (8)

Средняя ошибка аппроксимации не должна превышать 8–10%.

Для нашей модели средняя ошибка аппроксимации составляет: , что недопустимо велико.

5. Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера. Величина -критерия связана с коэффициентом детерминации , и ее можно рассчитать по следующей формуле:

.

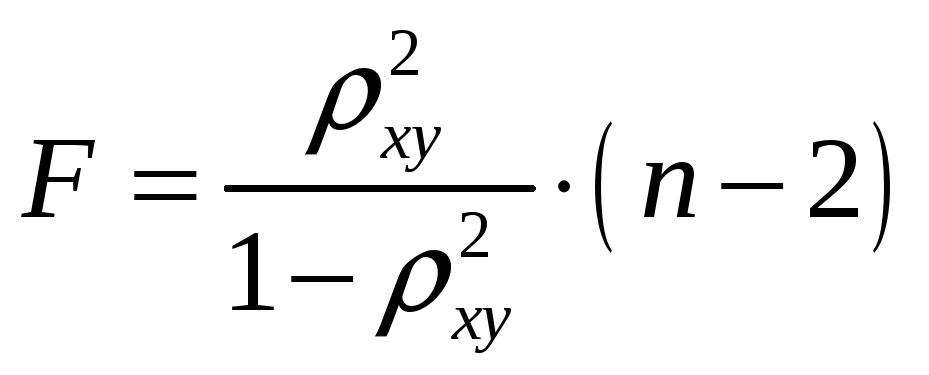Табличное значение . Так как , то признается статистическая значимость уравнения в целом.

ВЫВОД:

Сравним построенные модели по индексу детерминации и средней ошибке аппроксимации:

Таблица 6

Модель	Индекс детерминации, (, )	Средняя ошибка аппроксимации, , %
Линейная модель,	0,9648	10,13%
Степенная модель,	0,9649	12,39%
Гиперболическа модель:	0,6911	1,62%
Полулогарифмическая модель,	0,9023	0,10%
Экспоненциальная модель:	0,6844	30,83%

Из рассмотренных моделей хорошо исходные данные аппроксимирует полулогарифмическая модель, и её ошибка аппроксимации не превышает допустимый уровень. Так что можно сделать вывод о том, что полулогарифмическая модель является приемлемой.