2. Уравнение нелинейной регрессии всегда дополняется показателем тесноты связи – индексом корреляции :

Данный индекс показывает, что связь существует, но она незначительная.

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:

,

где .

Соответственно величина характеризует долю дисперсии , вызванную влиянием остальных, не учтенных в модели, факторов.

Индекс детерминации , показывает, что уравнением регрессии объясняется 90,23% дисперсии результативного признака, а на долю прочих факторов приходится малая часть дисперсии результативного признака 9,77%.

3. Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:

.

Так как коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора , то обычно рассчитывается средний коэффициент эластичности:

.

Для исследуемой модели . Т.е. при увеличении заработной платы на 1% от её среднего значения потребительские расходы увеличиваются на 1,6860% от своего среднего значения.

4. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

. (8)

Средняя ошибка аппроксимации не должна превышать 8–10%.

Для нашей модели средняя ошибка аппроксимации составляет: 0,10%, что является приемлемым.

5. Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера. Величина -критерия связана с коэффициентом детерминации , и ее можно рассчитать по следующей формуле:

.

Табличное значение . Так как , то признается статистическая значимость уравнения в целом.

1г. экспоненциальная модель: . Приведем данную модель к линейному виду: .

Таблица 4

	Y	x_t*Y_t	Y^2	Y_-	y-y_-	(y-y_-)^2
1	11,4863	81369,1611	131,9358	88093,1517	9282,3483	86161990,3395	0,0953
2	10,8179	66119,2774	117,0279	99194,9512	-49286,5512	2429164133,7684	-0,9875
3	10,9913	62485,4930	120,8085	104504,3507	-45149,3507	2038463869,7033	-0,7607
4	10,9783	77067,7177	120,5232	88784,3085	-30195,0085	911738540,6425	-0,5154
5	10,6340	47480,6718	113,0813	121292,4612	-79770,8612	6363390291,0928	-1,9212
6	11,2009	78339,2963	125,4608	89066,6376	-15868,2376	251800963,3664	-0,2168
7	11,0544	68846,7324	122,1995	97799,7666	-34578,9666	1195704934,2781	-0,5470
8	11,2009	75124,2632	125,4596	92243,4069	-19049,0069	362864662,8717	-0,2603
9	11,7208	90320,8497	137,3783	81649,9722	41461,7278	1719074869,3690	0,3368
10	11,5736	124972,2507	133,9493	55973,1941	50287,2059	2528803074,0900	0,4732
11	11,1446	65474,3470	124,2014	102107,6379	-32920,5379	1083761813,6928	-0,4758
12	11,1760	69012,0763	124,9040	98434,7702	-27035,3702	730911242,4193	-0,3786
13	11,1205	76408,9790	123,6656	90414,4892	-22872,5892	523155338,0213	-0,3386
14	10,9461	75199,7970	119,8174	90425,5305	-33692,4305	1135179876,1256	-0,5939
15	11,1123	81241,8407	123,4827	85684,8045	-18696,4045	349555539,7660	-0,2791
16	11,1198	73791,1397	123,6504	93046,6260	-25550,7260	652839600,1081	-0,3786
17	11,4950	93730,0371	132,1345	77303,2156	20917,8844	437557889,2964	0,2130
18	12,8599	383265,0360	165,3783	5496,6837	379099,1163	143716140008,0340	0,9857
сумма	202,6328	1690248,9662	2285,0585	1561515,9584	66382,2416	166516268636,9850	-5,5494
ср. знач	11,2574	93902,7203	126,9477	86750,8866	3687,9023	9250903813,1659	30,83%

Оценки параметров приведенной модели рассчитываются аналогично оценкам параметров линейной модели:

.

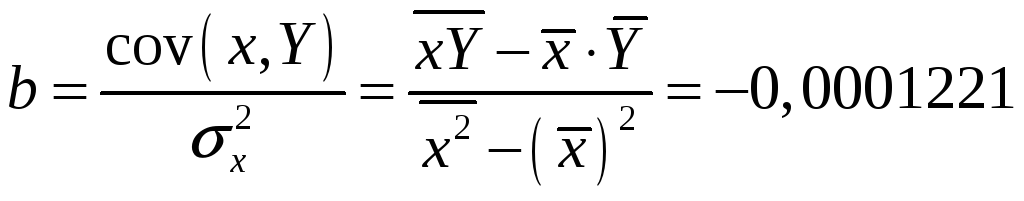
Т.е. получаем следующее уравнение: , которое после потенцирования примет вид: