Лабораторная работа №2
Тема: «Нелинейная регрессия»
Задание:
По данным первой лабораторной работы
-
Рассчитайте параметры уравнений степенной, экспоненциальной, полулогарифмической, обратной и гиперболической парной регрессии..
-
Оцените тесноту связи с помощью показателей корреляции и детерминации.
-
Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
-
Оцените качество уравнений с помощью средней ошибки аппроксимации.
-
Оцените статистическую надежность результатов регрессионного моделирования с помощью
- критерия Фишера. По значениям
характеристик, полученных в предыдущих
заданиях, выберите лучшее уравнение
регрессии и дайте его обоснование.
Решение:
1а. Среди нелинейных моделей наиболее
часто используется степенная функция
,
которая приводится к линейному виду
путем логарифмирования:
;
;
,
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
1 |
11,4863 |
8,8656 |
101,8331 |
131,9358 |
78,5988 |
74397,9004 |
22977,5996 |
527970085,1200 |
0,2360 |
|
2 |
10,8179 |
8,7180 |
94,3109 |
117,0279 |
76,0037 |
62785,2515 |
-12876,8515 |
165813304,4325 |
0,2580 |
|
3 |
10,9913 |
8,6456 |
95,0262 |
120,8085 |
74,7462 |
57768,3541 |
1586,6459 |
2517445,2862 |
0,0267 |
|
4 |
10,9783 |
8,8565 |
97,2296 |
120,5232 |
78,4379 |
73625,5275 |
-15036,2275 |
226088136,4719 |
0,2566 |
|
5 |
10,6340 |
8,4040 |
89,3681 |
113,0813 |
70,6276 |
43757,7708 |
-2236,1708 |
5000460,0199 |
0,0539 |
|
6 |
11,2009 |
8,8528 |
99,1597 |
125,4608 |
78,3722 |
73312,0518 |
-113,6518 |
12916,7363 |
0,0016 |
|
7 |
11,0544 |
8,7368 |
96,5801 |
122,1995 |
76,3319 |
64157,4160 |
-936,6160 |
877249,5263 |
0,0148 |
|
8 |
11,2009 |
8,8109 |
98,6899 |
125,4596 |
77,6321 |
69863,4913 |
3330,9087 |
11094952,6795 |
0,0455 |
|
9 |
11,7208 |
8,9498 |
104,8987 |
137,3783 |
80,0981 |
81957,7492 |
41153,9508 |
1693647669,1880 |
0,3343 |
|
10 |
11,5736 |
9,2871 |
107,4858 |
133,9493 |
86,2505 |
120799,9492 |
-14539,5492 |
211398491,7365 |
0,1368 |
|
11 |
11,1446 |
8,6785 |
96,7177 |
124,2014 |
75,3157 |
59993,9656 |
9193,1344 |
84513719,4336 |
0,1329 |
|
12 |
11,1760 |
8,7283 |
97,5475 |
124,9040 |
76,1826 |
63529,9991 |
7869,4009 |
61927470,7830 |
0,1102 |
|
13 |
11,1205 |
8,8351 |
98,2504 |
123,6656 |
78,0584 |
71831,4475 |
-4289,5475 |
18400217,8747 |
0,0635 |
|
14 |
10,9461 |
8,8349 |
96,7080 |
119,8174 |
78,0558 |
71819,4263 |
-15086,3263 |
227597240,0129 |
0,2659 |
|
15 |
11,1123 |
8,8971 |
98,8674 |
123,4827 |
79,1590 |
77145,7965 |
-10157,3965 |
103172704,0474 |
0,1516 |
|
16 |
11,1198 |
8,8003 |
97,8574 |
123,6504 |
77,4447 |
69013,7349 |
-1517,8349 |
2303822,9168 |
0,0225 |
|
17 |
11,4950 |
9,0063 |
103,5268 |
132,1345 |
81,1128 |
87460,2092 |
10760,8908 |
115796770,0816 |
0,1096 |
|
18 |
12,8599 |
10,3024 |
132,4879 |
165,3783 |
106,1387 |
388218,7980 |
-3622,9980 |
13126114,5334 |
0,0094 |
|
сумма |
202,6328 |
160,2099 |
1806,5451 |
2285,0585 |
1428,5666 |
|
|
3471258770,8806 |
2,2298 |
|
ср. знач |
11,2574 |
8,9005 |
100,3636 |
126,9477 |
79,3648 |
|
|
192847709,4934 |
12,39% |
Оценки параметров приведенной модели рассчитываются аналогично оценкам параметров линейной модели:
.
Т.е. получаем следующее
уравнение:
,
которое после потенцирования примет
вид:
2. Уравнение нелинейной регрессии всегда дополняется показателем тесноты связи – индексом корреляции :
Данный индекс показывает, что связь существует, но она незначительная.
Квадрат индекса корреляции носит
название индекса детерминации и
характеризует долю дисперсии
результативного признака
,
объясняемую регрессией, в общей дисперсии
результативного признака:
,
где
.
Соответственно величина
характеризует долю дисперсии
,
вызванную влиянием остальных, не учтенных
в модели, факторов.
Индекс детерминации
,
показывает, что уравнением регрессии
объясняется 96,49% дисперсии результативного
признака, а на долю прочих факторов
приходится малая часть дисперсии
результативного признака - 3,51%.
3. Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
.
Так как коэффициент эластичности не
является постоянной величиной, а зависит
от соответствующего значения фактора
,
то обычно рассчитывается средний
коэффициент эластичности:
.
Для исследуемой модели
.
Т.е. при увеличении заработной платы на
1% от её среднего значения потребительские
расходы увеличиваются на 1,1499% от своего
среднего значения.
4. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:
. (8)
Средняя ошибка аппроксимации не должна превышать 8–10%.
Для нашей модели средняя ошибка
аппроксимации составляет:
,
что недопустимо велико.
5. Оценка значимости уравнения регрессии
в целом производится на основе
-критерия
Фишера. Величина
-критерия
связана с индексом детерминации
,
и ее можно рассчитать по следующей
формуле:
.
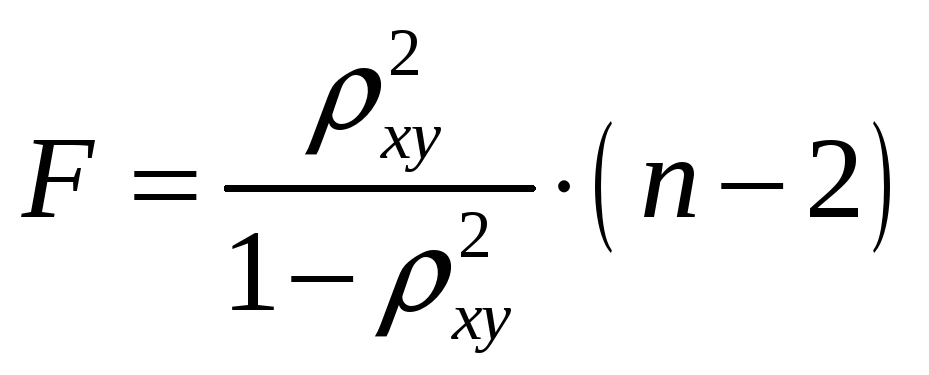Табличное значение
.
Так как
,
то признается статистическая значимость
уравнения в целом.
1б. Следующая модель – гиперболическая:
.
Сделаем замену
,
и приведем модель к линейному виду:
Таблица 2
|
|
|
|
|
|
|
|
|
|
|
1 |
0,000141 |
13,7458 |
0,0000000199 |
94881,29571 |
2494,204288 |
6221055,031 |
|
|
|
2 |
0,000164 |
8,1656 |
0,0000000268 |
57558,0121 |
-7649,612103 |
58516565,32 |
-0,153273038 |
|
|
3 |
0,000176 |
10,4406 |
0,0000000309 |
37127,01612 |
22227,98388 |
494083267,6 |
0,374492189 |
|
|
4 |
0,000142 |
8,3461 |
0,0000000203 |
92741,66025 |
-34152,36025 |
1166383711 |
-0,582911218 |
|
|
5 |
0,000224 |
9,2994 |
0,0000000502 |
-42779,71719 |
84301,31719 |
7106712080 |
2,030300306 |
|
|
6 |
0,000143 |
10,4659 |
0,0000000204 |
91861,24798 |
-18662,84798 |
348301894,7 |
-0,254962513 |
|
|
7 |
0,000161 |
10,1511 |
0,0000000258 |
62624,43593 |
596,3640664 |
355650,0996 |
0,009433036 |
|
|
8 |
0,000149 |
10,9131 |
0,0000000222 |
81689,31616 |
-8494,916162 |
72163600,59 |
-0,116059646 |
|
|
9 |
0,000130 |
15,9761 |
0,0000000168 |
113824,7121 |
9286,987895 |
86248144,16 |
0,075435461 |
|
|
10 |
0,000093 |
9,8407 |
0,0000000086 |
175603,9626 |
-69343,56265 |
4808529681 |
-0,652581419 |
|
|
11 |
0,000170 |
11,7765 |
0,0000000290 |
46584,82947 |
22602,27053 |
510862633,2 |
0,326683306 |
|
|
12 |
0,000162 |
11,5627 |
0,0000000262 |
60333,22126 |
11066,17874 |
122460311,9 |
0,1549898 |
|
|
13 |
0,000146 |
9,8300 |
0,0000000212 |
87605,90066 |
-20064,00066 |
402564122,4 |
-0,297060057 |
|
|
14 |
0,000146 |
8,2581 |
0,0000000212 |
87570,67989 |
-30837,57989 |
950956333,7 |
-0,543555348 |
|
|
15 |
0,000137 |
9,1627 |
0,0000000187 |
102168,2492 |
-35179,84922 |
1237621791 |
-0,5251633 |
|
|
16 |
0,000151 |
10,1712 |
0,0000000227 |
79037,15969 |
-11541,25969 |
133200675,2 |
-0,170992011 |
|
|
17 |
0,000123 |
12,0458 |
0,0000000150 |
125678,408 |
-27457,30797 |
753903761,1 |
-0,279545922 |
|
|
18 |
0,000034 |
12,9046 |
0,0000000011 |
273787,81 |
110807,99 |
12278410645 |
0,288115445 |
|
|
сумма |
0,002589 |
193,0559 |
0,000000397 |
1627898,20 |
|
30537495922,171300 |
-0,291041 |
|
|
ср. знач |
0,000144 |
10,7253 |
0,000000022 |
90438,788889 |
|
1696527551,231740 |
1,62% |
Оценки параметров приведенной модели рассчитываются аналогично оценкам параметров линейной модели:
.
Т.е. получаем следующее уравнение:
