
Операторы в квантовой механике
-
Найти собственные функции и собственные значения следующих операторов: а)
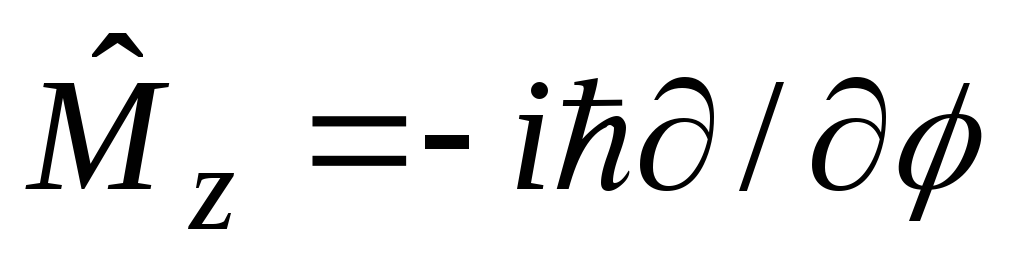 ,
(
,
( -
азимутальный угол); б)
-
азимутальный угол); б)
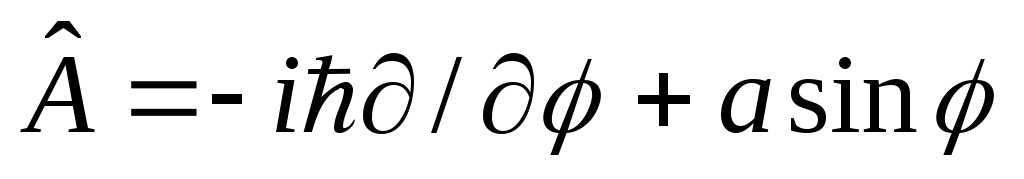 ;
в)
;
в)
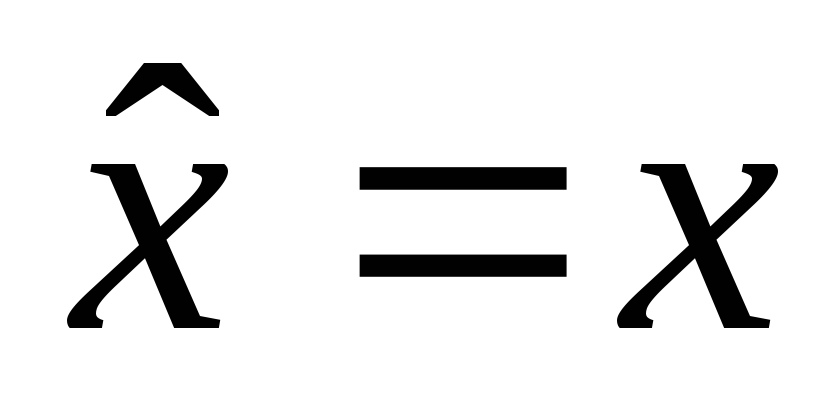 .
.
-
Найти собственные функции и собственные значения оператора отражения координат:
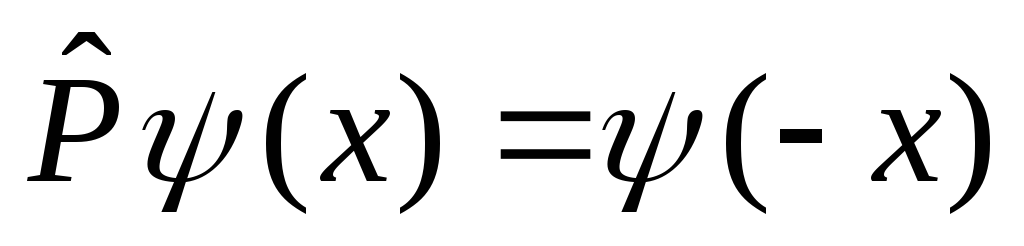 .
.
-
Найти явный вид оператора трансляции
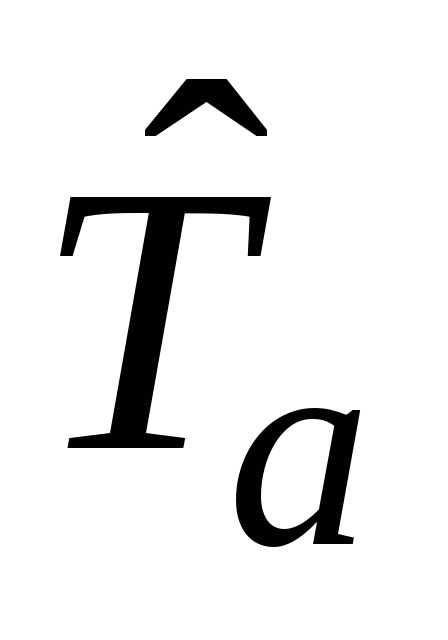 на конечное расстояние
на конечное расстояние
 :
:
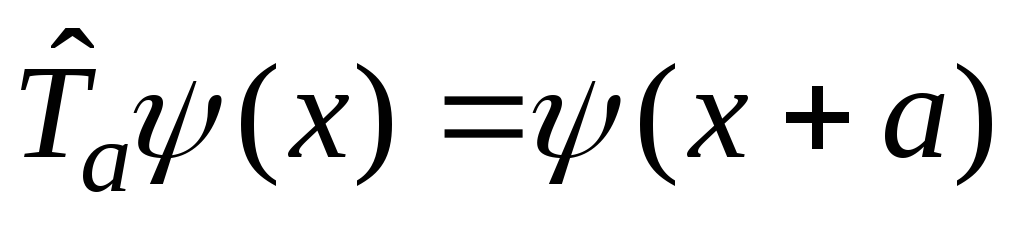 ,
выразить его через оператор
,
выразить его через оператор
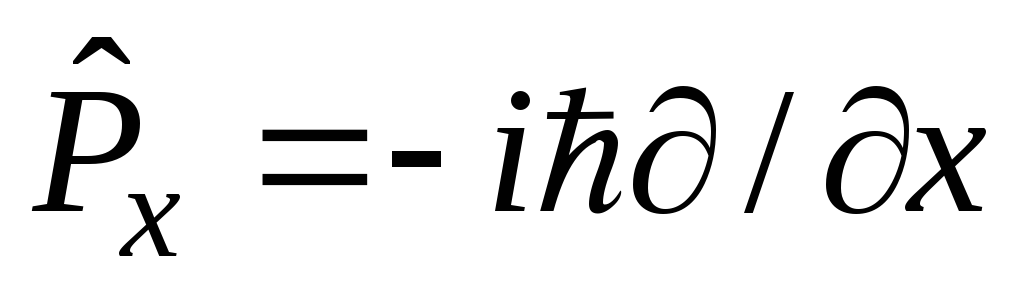 проекции импульса на направление
проекции импульса на направление
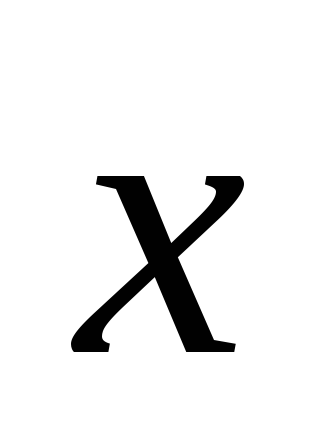 .
Найти собственные функции и собственные
значения оператора
.
Найти собственные функции и собственные
значения оператора
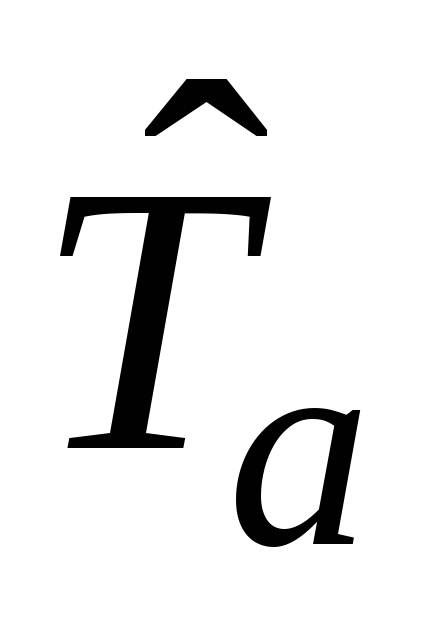 .
.
-
Найти явный вид оператора поворота
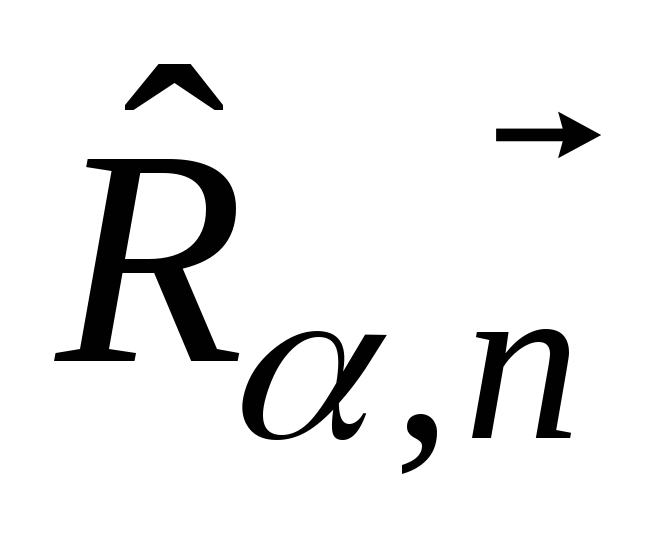 на конечный угол
на конечный угол
 вокруг направления
вокруг направления
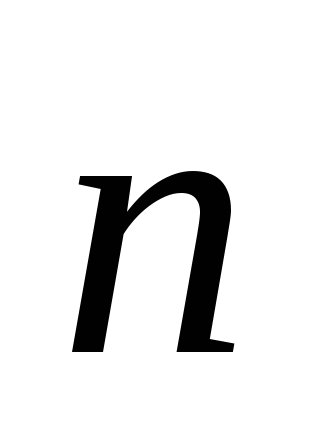 и выразить его через оператор
и выразить его через оператор
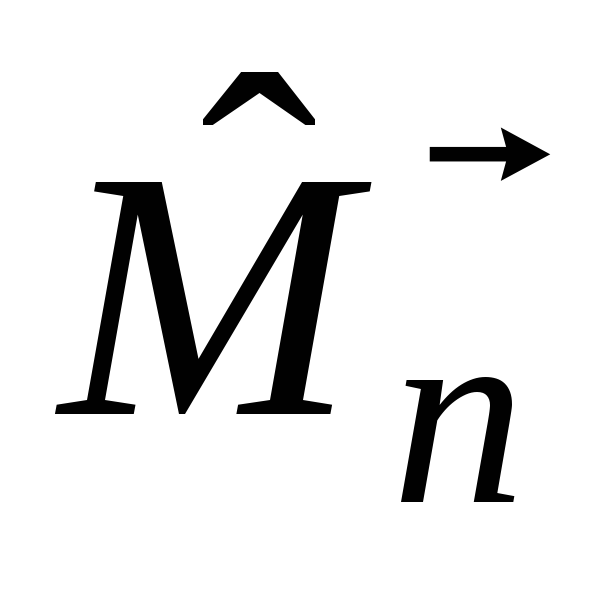 проекции момента импульса на направление
проекции момента импульса на направление
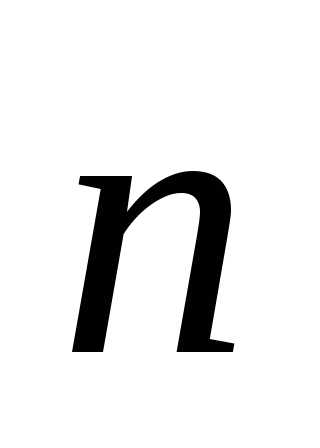 .
Найти собственные функции и собственные
значения оператора
.
Найти собственные функции и собственные
значения оператора
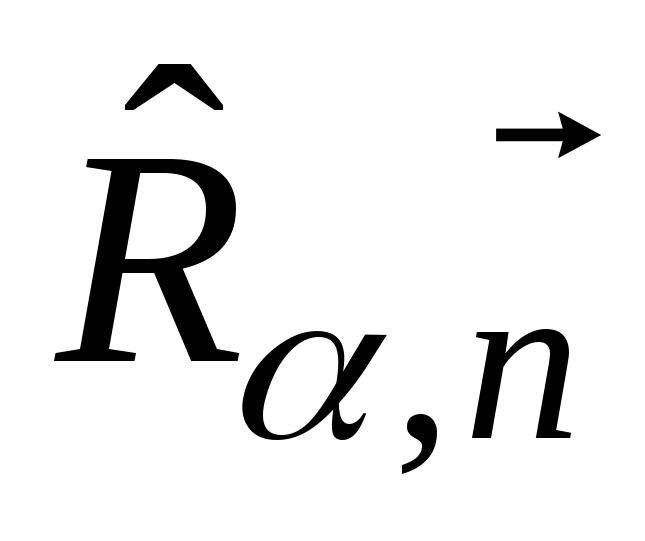 .
.
-
Показать, что собственные функции унитарного оператора ортогональны, а собственные значения в общем случае комплексны и по модулю равны единице.
-
Показать, что собственные функции эрмитового оператора ортогональны (либо могут быть ортогонализованы), а собственные значения действительны.
-
Вычислить коммутаторы:
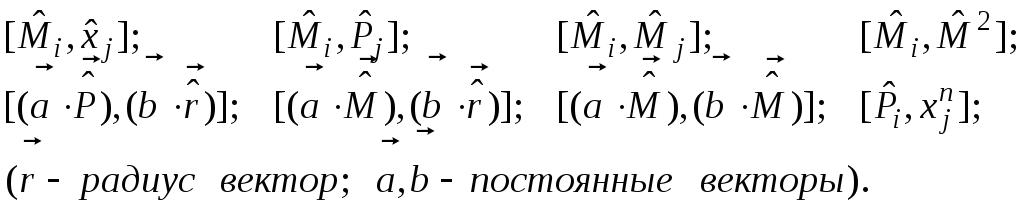
Стационарные состояния.
-
Найти волновые функции частицы в одномерном потенциальном поле вида
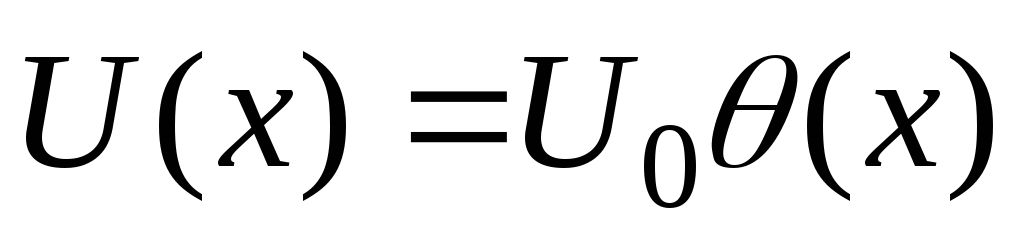 в зависимости от ее энергии
в зависимости от ее энергии
 .
Для случая
.
Для случая
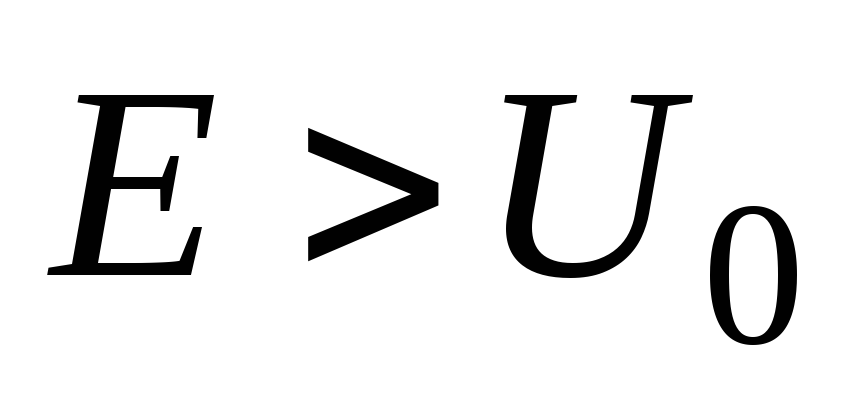 вычислить коэффициенты отражения и
прохождения для потоков, падающих на
вычислить коэффициенты отражения и
прохождения для потоков, падающих на
 -образный
барьер слева и справа.
-образный
барьер слева и справа.
-
Найти волновые функции и энергии связанных
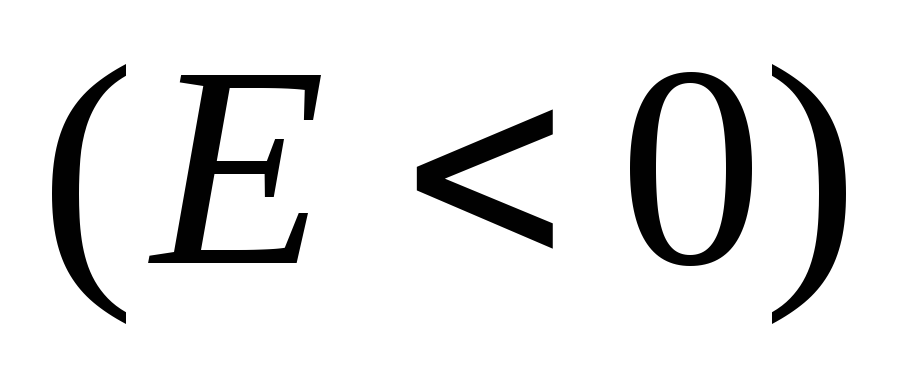 состояний частицы в потенциальной яме
вида
состояний частицы в потенциальной яме
вида
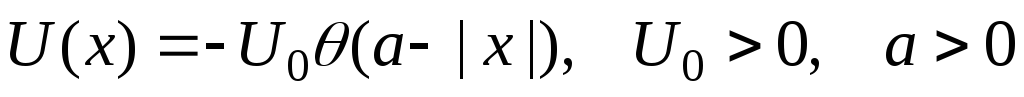 .
Для энергий непрерывного спектра
.
Для энергий непрерывного спектра
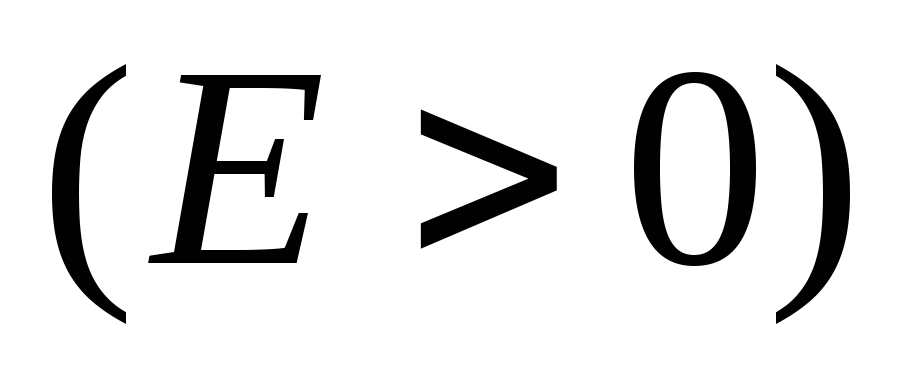 вычислить коэффициенты отражения от
ямы и прохождения через нее.
вычислить коэффициенты отражения от
ямы и прохождения через нее.
-
Решить стационарное уравнение Шредингера в одномерном потенциальном поле вида:
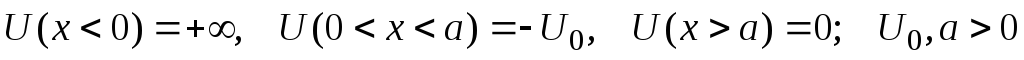 .
. -
Вычислить коэффициенты отражения и прохождения частицы для потенциального барьера вида
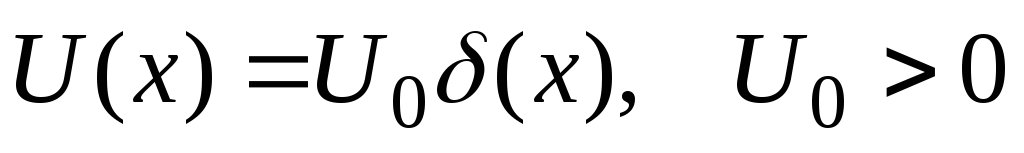 и для потенциальной ямы вида
и для потенциальной ямы вида
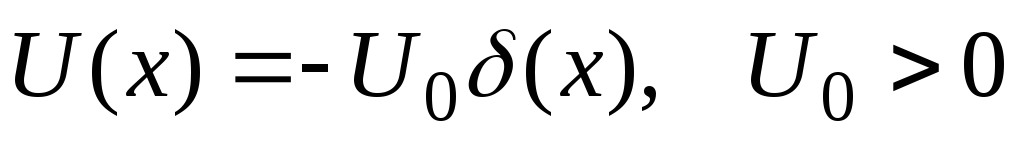 .
.
-
Вычислить коэффициенты отражения и прохождения частицы для потенциалов вида: а)
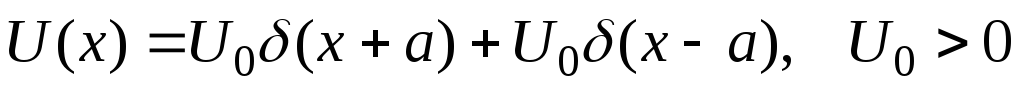 ,
б)
,
б)
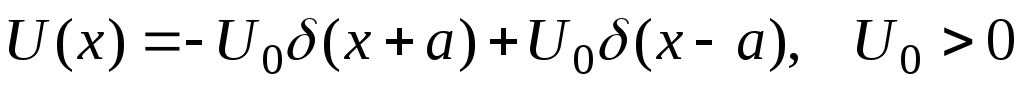 .
.
-
Найти волновые функции и энергии связанных
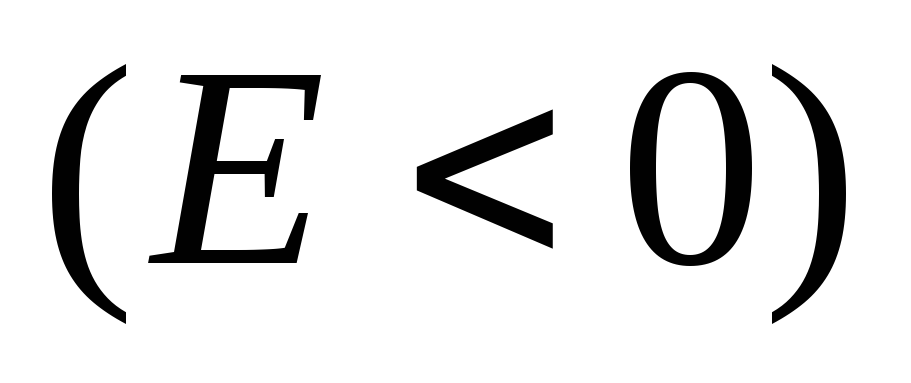 состояний частицы в потенциальном поле
вида
состояний частицы в потенциальном поле
вида
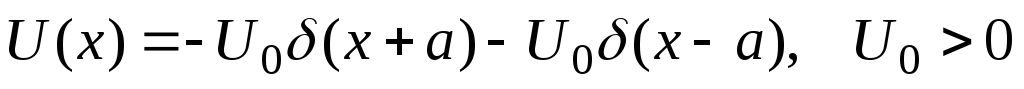 .
Для энергий непрерывного спектра
.
Для энергий непрерывного спектра
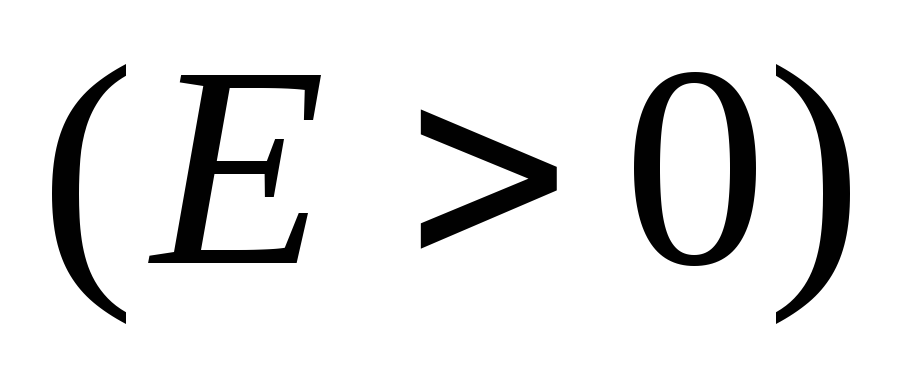 вычислить коэффициенты отражения от
потенциала и прохождения через него.
вычислить коэффициенты отражения от
потенциала и прохождения через него.
-
Найти уровни энергии и волновые функции частицы, находящейся в бесконечно глубокой потенциальной яме, разделенной
 -образным
потенциальным барьером:
-образным
потенциальным барьером:
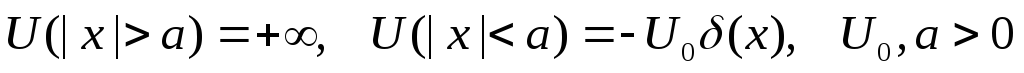 .
.
-
Найти уровни энергии и волновые функции частицы, находящейся в бесконечно глубокой потенциальной яме вида:
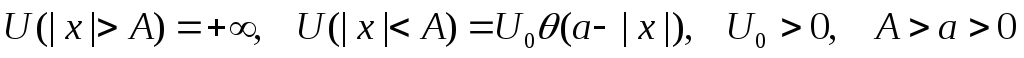 .
Рассмотреть случаи, когда энергия
.
Рассмотреть случаи, когда энергия
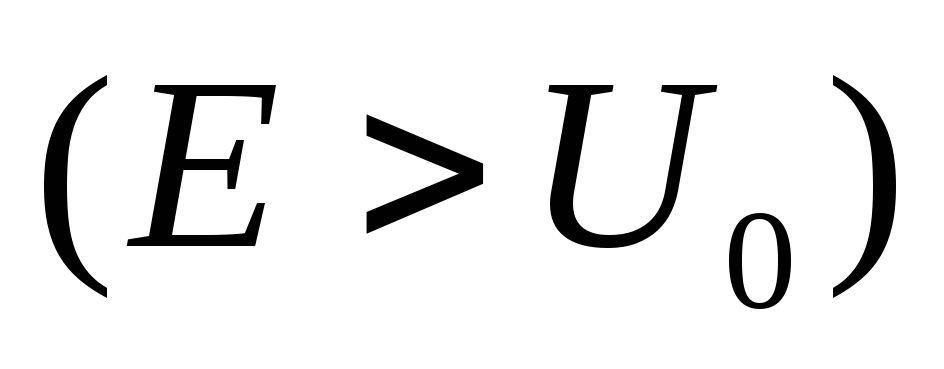 и
и
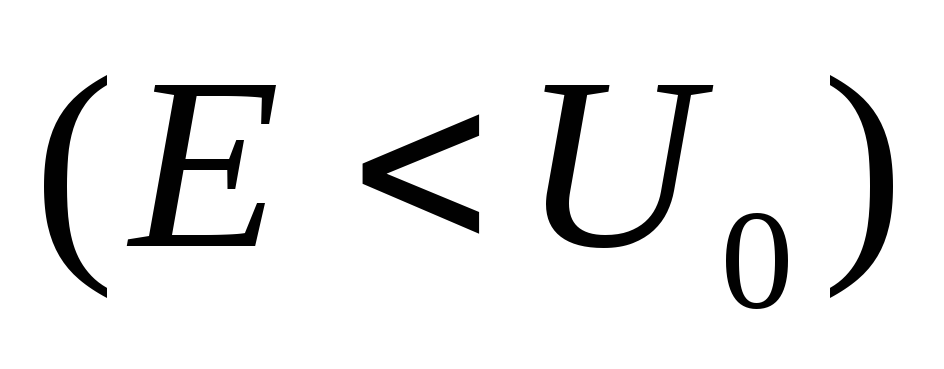 .
.
Принцип суперпозиции. Соотношение неопределенностей.
-
Найти среднее значение энергии заряженной частицы, находящейся в состоянии
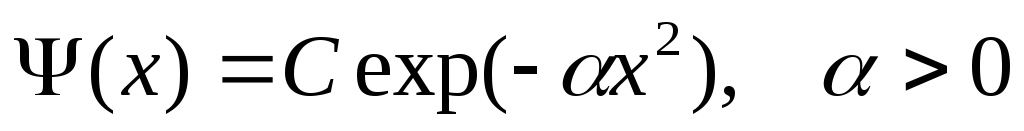 ,
под действием постоянного электрического
поля
,
под действием постоянного электрического
поля
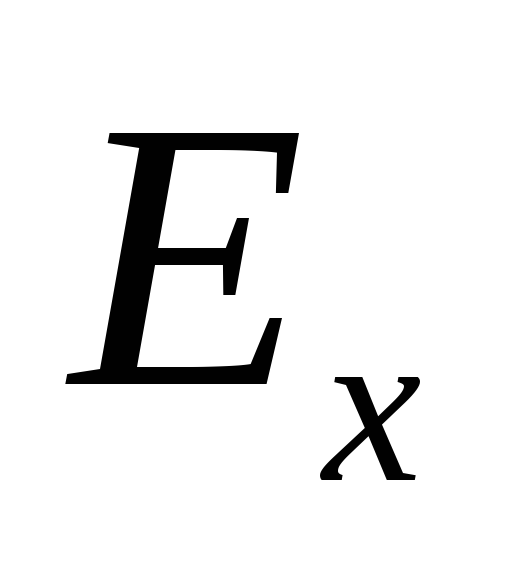 .
.
-
Определить волновую функцию свободной частицы, находящейся в стационарном состоянии с энергией
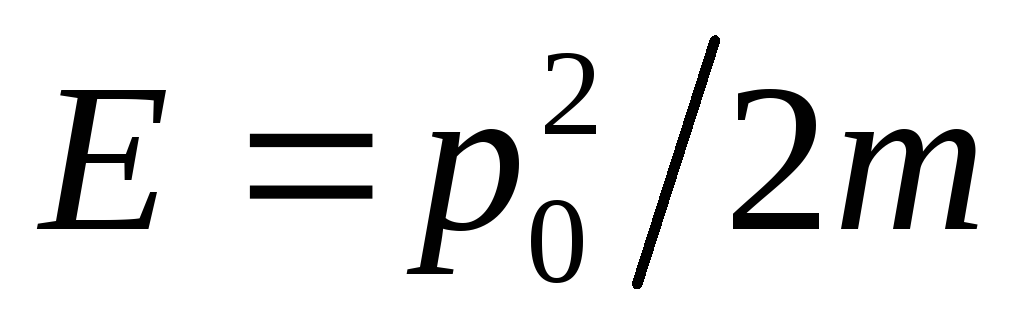 и средним значением импульса
и средним значением импульса
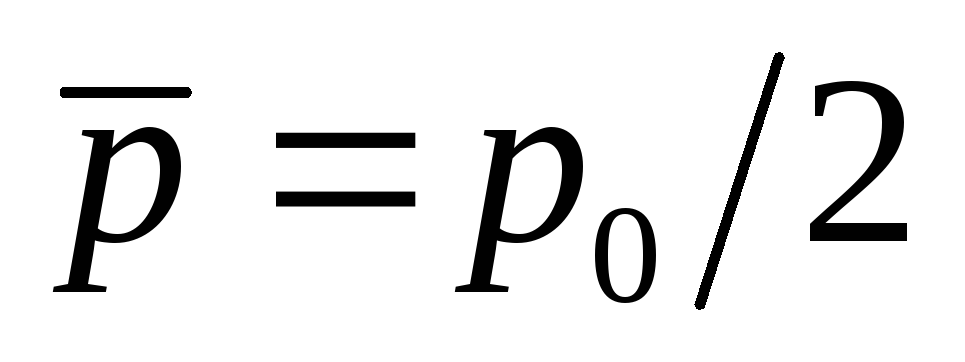 .
Является ли решение задачи однозначным?
.
Является ли решение задачи однозначным?
-
Доказать, что при движении в симметричном поле
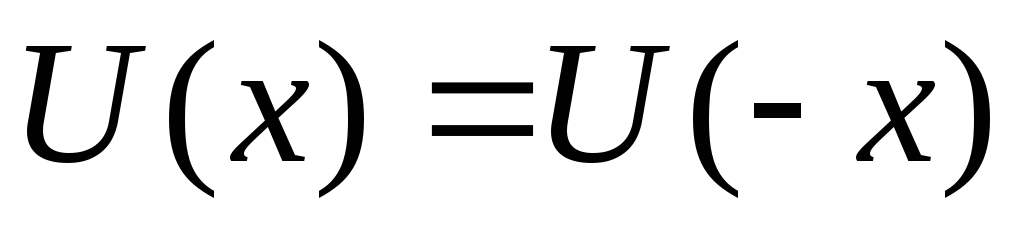 средние значения координаты и импульса
средние значения координаты и импульса
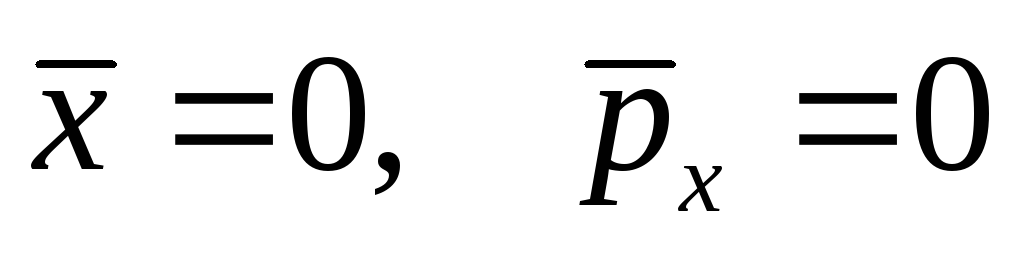 для любого стационарного состояния
дискретного спектра.
для любого стационарного состояния
дискретного спектра.
-
Волновая функция свободной частицы в импульсном
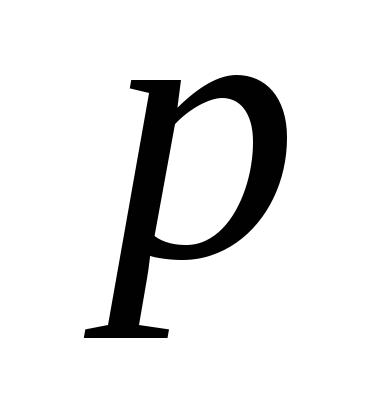 -
представлении в некоторый момент
времени
-
представлении в некоторый момент
времени
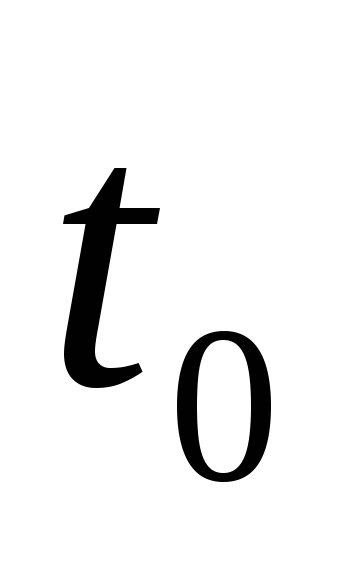 имеет вид
имеет вид
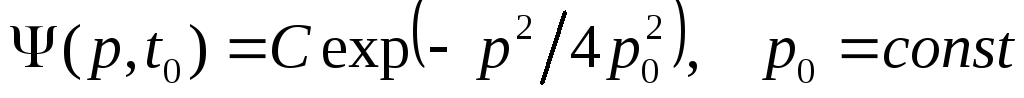 .
Найти средние значения
.
Найти средние значения
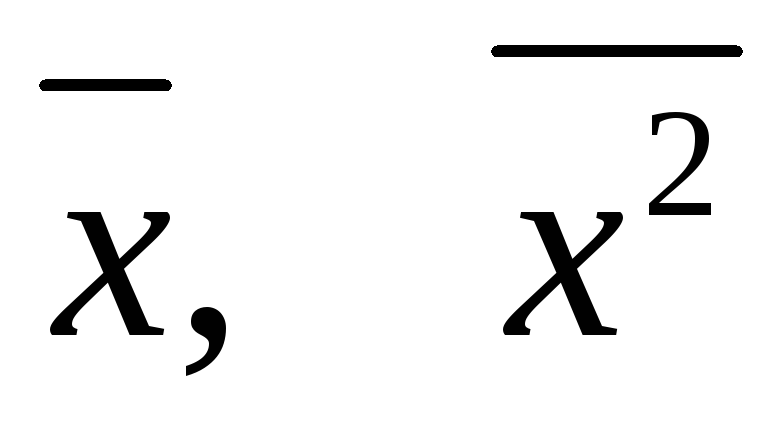 в этом состоянии и проверить соотношение
неопределенностей. Будет ли распределение
по координатам меняться с течением
времени?
в этом состоянии и проверить соотношение
неопределенностей. Будет ли распределение
по координатам меняться с течением
времени?
-
Частица находится в состоянии с волновой функцией:
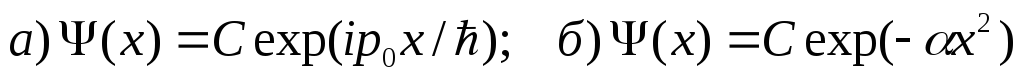 .
Какой результат даст измерение импульса
в этом состоянии?
.
Какой результат даст измерение импульса
в этом состоянии?
-
Волновая функция гармонического осциллятора в некоторый момент времени
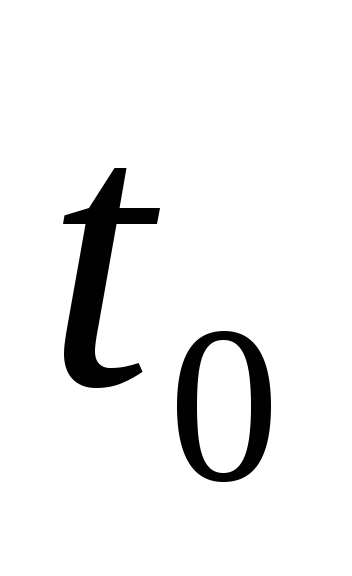 имеет вид
имеет вид
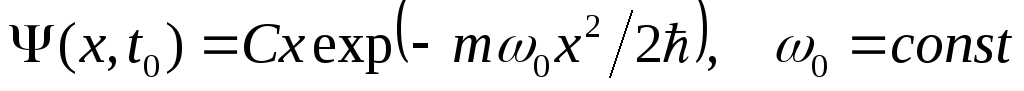 .
Найти распределение по импульсам в
момент времени
.
Найти распределение по импульсам в
момент времени
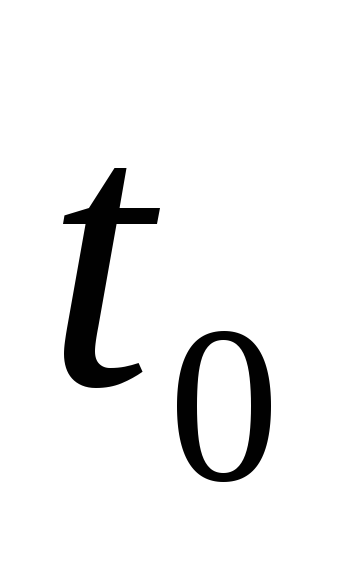 и волновую функцию
и волновую функцию
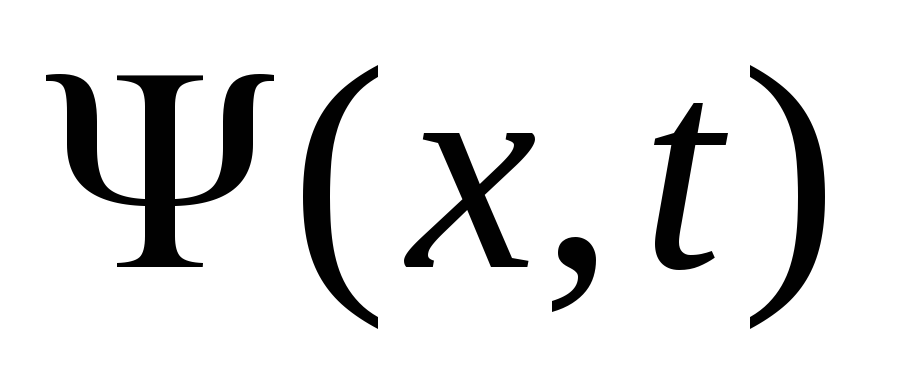 в
произвольный момент времени
в
произвольный момент времени
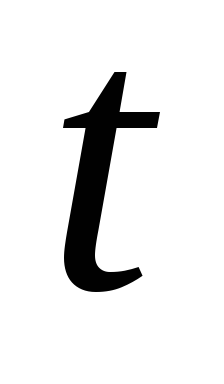 .
Как будет изменяться распределение по
импульсам с течением времени?
.
Как будет изменяться распределение по
импульсам с течением времени?
-
Волновая функция частицы имеет вид
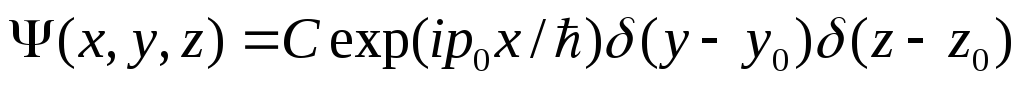 .
Существуют ли в этом состоянии
определенные координаты, энергия,
проекции импульса частицы? Какое
распределение вероятностей имеют
импульс и кинетическая энергия? Чему
равно среднее значение импульса и его
дисперсия? Чему равно среднее значение
кинетической энергии?
.
Существуют ли в этом состоянии
определенные координаты, энергия,
проекции импульса частицы? Какое
распределение вероятностей имеют
импульс и кинетическая энергия? Чему
равно среднее значение импульса и его
дисперсия? Чему равно среднее значение
кинетической энергии?
-
Определить распределение вероятностей по импульсам для частицы, находящейся в основном состоянии в бесконечно глубокой потенциальной яме
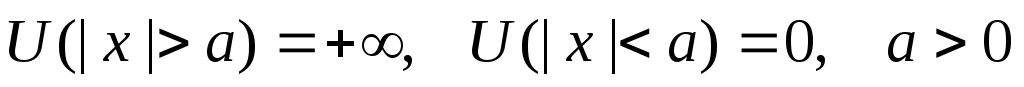 .
.
-
Исходя из соотношения неопределенностей, оценить энергию основного состояния частицы в потенциальных полях вида:
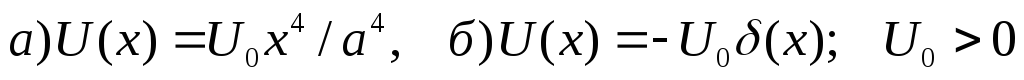 .
.
-
Свободная частица движется в пространстве с энергией
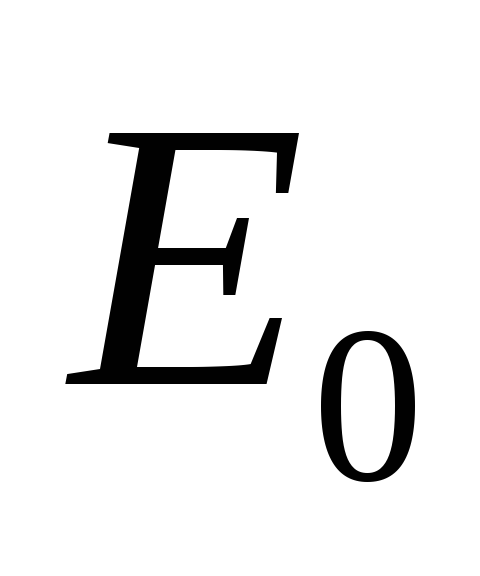 .
Существует ли у такой частицы определенный
импульс? Какие значения импульса и с
какими вероятностями будут наблюдаться
у такой частицы при измерении? Определить
среднее значение и дисперсию импульса
частицы. Движение считать одномерным.
.
Существует ли у такой частицы определенный
импульс? Какие значения импульса и с
какими вероятностями будут наблюдаться
у такой частицы при измерении? Определить
среднее значение и дисперсию импульса
частицы. Движение считать одномерным.
