1. С

   Исследование операций

   одержание математического программирования. Постановка общей и основной задач линейного программирования.

Линейное программирование является основным разделом математического программирования. Термин математическое программирование появился приблизительно в 1950 г., его пред­ложил математик Р. Дорфман. Содержание математического про­граммирования составляют теория и методы решения задач о на­хождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и/или неравенствами). Математическое программирование является од­ним из разделов науки об исследовании операций.

К задачам линейного программирования относятся задачи, в которых требуется найти максимальное или минимальное зна­чение некоторой линейной целевой функции на множестве, опре­деляемом системой линейных равенств или неравенств. В линей­ном программировании существует класс задач, структура кото­рого позволяет создать специальные методы их решения, выгод­но отличающиеся от методов решения задач общего характера. Так в линейном программировании появился раздел транспорт­ных задач.

Наиболее исследованной областью математического про­граммирования является линейное программирование. Получен­ные результаты столь значительны, что достигнутый здесь уро­вень позволяет решать большинство практических задач.

При выборе наиболее подходящего способа описания ре­альных процессов приходится сталкиваться с рядом трудностей, которые можно подразделить на две группы. Одна группа связана с построением математической модели процесса, а другая - с ме­тодами решения этой модели. Теория математических моделей является предметом специального курса и требует от исследова­теля знания той области, которой принадлежит моделируемый объект. Здесь же будут рассмотрены традиционные примеры, ил­люстрирующие применение метода математического моделиро­вания в экономических задачах.

Для практического решения экономической задачи матема­тическими методами прежде всего ее следует записать с помо­щью математических выражений (уравнений, неравенств и т. п.),

т. е. составить экономико-математическую: модель. Приведем общую схему формирования такой модели:

1) выбор некоторого числа переменных величин, заданием чи­словых значений которых однозначно определяется одно из воз­можных состояний исследуемого явления;

2) выражение взаимосвязей, присущих решению, в виде мате­матических соотношений (уравнений, неравенств). Эти соотно­шения образуют систему ограничений задачи

3) количественное выражение выбранного критерия опти­мальности в форме целевой функции;

4) математическая формулировка задали как задачи нахождения экстремума целевой функции при условии выполнения ограничений накладываемых на переменные.

Общая и основная задачи линейного программирования.

Общая задача. Найти максимальное значение линейной целевой функции.

z = c₁x₁ + c₂x₂ + … + c_nx_n

при линейных ограничениях

x_j >= 0, j = 1, n = {1,2,…,n}

Определение 1.1. Совокупность чисел х = (х₁, х₂,..., х_n), удовлетворяющих ограничениям (1.2), называется допустимым решением или планом.

Определение 1.2. План х* =(х₁^*, х₂^*,...,х_n*), при котором целевая функция (1.1) принимает свое максимальное значение, называется оптимальным.

Каноническая форма. Задачу линейного программирова­ния будем считать приведенной к каноническому виду, если

1) требуется найти максимум целевой функции;

2) система ограничений (1.2) содержи! только равенства;

3) правые части системы ограничений неотрицательны.

Переход от общей формы к канонической:

1) если в задаче требуется найти минимум целевой функции, то вводим новую целевую функцию z₁ = -z, тогда max z₁ = -min z;

2) чтобы перейти от неравенства к равенству в системе огра­ничений, необходимо прибавить (вычесть) дополнительную не­отрицательную переменную к левой части неравенства;

3) если в правой части системы ограничений имеются отрица­тельные числа, то необходимо умножить на "-1" обе части равен­ства, в котором в правой части стоит отрицательное число.

Задачу линейного программирования в канонической фор­ме называют основной задачей.

2. Свойства задач линейного программирования. Графический метод решения задач линейного программирования.

Свойства задач линейного программирования.

Рассмотрим следующую основную задачу линейного про­граммирования:

z = c₁x₁ + c₂x₂ + … + c_nx_n  max

при ограничениях

,

Перепишем ограничения этой задачи к немирной форме:

x₁Р,+х₂Р₂+... + х _n Р _n , (1.3)

где Р₁, ,...,Р_n и Р₀ - k-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членах системы ограничений основной задачи:

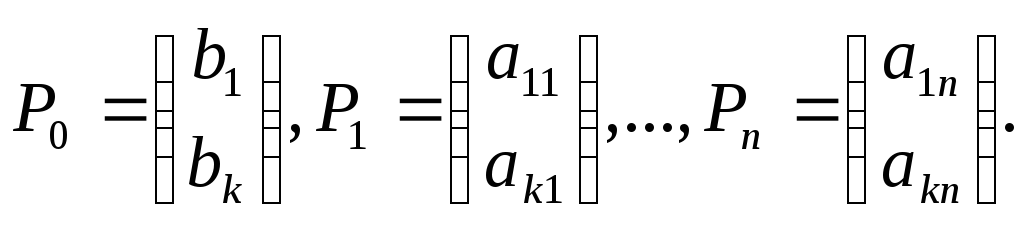
Определение 1. План х = (x₁,х₂,...,х_n) называется

опорным планом основной задачи линейного программирования, если его положительные коэффициенты (х_j >0) стоят при линейно независимых векторах Р_j.

Так как векторы Р: являются k-мерными, то из определения

опорного плана следует, что число его положительных компо­нент не может быть больше числа К.

Определение 2. Опорный план называется невырож­денным, если он содержит ровно k положительных компонент, в противном случае он называется вырожденным.

Свойства задач линейного программирования тесным обра­зом связаны со свойствами выпуклых множеств.

Определение 3. Пусть х^(|),...х^(m) - произвольные точ­ки евклидова пространства Rⁿ. Выпуклой линейной комбинацией этих точек называется сумма: а,х^(|) + ...+ а_mх^(m), где а_i; -про­извольные неотрицательные числа, сумма которых равна 1.

Определение 4. Множество называется выпуклым, ес­ли вместе с любыми двумя своими точками оно содержит и отре­зок прямой, соединяющий эти точки.

Определение 5. Точка х выпуклого множества назы­вается угловой, если она не может быть представлена в виде вы­пуклой линейной комбинации каких-нибудь двух других различ­ных точек данного множества.

Сформулируем первое свойство задач ЛП.

Теорема 1.1. Множество планов любой задачи линейного программирования является выпуклым (если оно не пусто).

Определение 7. Непустое множество планов задачи линейного программирования называется многогранником реше­ний, а всякая угловая точка многогранника решений — вершиной.

Сформулируем второе свойство задач ЛП.

Теорема 1.2. Если задача линейного программирования имеет оптимальный план, то экстремальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если экстремальное значение целевая функция прини­мает более чем в одной вершине, то она принимает его на ребре (грани), содержащем эти вершины.

Теорема 1.3. Если система векторов Р₁,...Р_m () ли­нейно независима и такова, что

х₁Р₁₊... + х_mР_m=Р₀,

где все х_j >= 0, то точка х = (х,, х₂,..., х_т,0,...,0) является верши­ной многогранника решений.

Теорема 1.4. Если х = (х,,х₂,..., х_п) - вершина многогран­ника решений, то векторы Р_j , соответствующие положительным х_j > 0, линейно независимы.