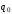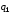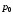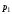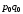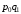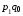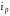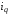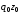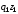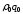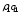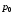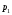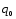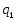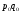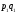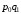Дом статистика

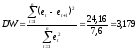
Так как коэффициент Дарбина-Уотсона находится не в пределах до 2,5 (DW = 3,179), то отклонение уровней от тенденции (так называемые остатки) неслучайны и есть основания утверждать, что условия выполняются, выполнение которых предполагалось при оценивании уравнения тренда, и, следовательно, нет оснований для дополнительных исследований.

Задание 2

Задача 1. Рассмотрим индексный метод изучения динамики сложных статистических совокупностей по данным о ценах и реализации товаров за два периода.

Информация и расчет внесены в табл. 10.

Таблица 10

Товар	Ед. изм.	Количество единиц			Цена единицы, р.			Стоимость (товарооборот), р.					Индекс
		баз. пер.	отч. пер.	баз. пер.		отч. Пер	баз. пер.		отч. пер.	условн.	условн.	цены		физ. объема
C	шт.	1000	750	30		40	30000		30000	22500	40000	1,3		0,75
D	м.	2000	1800	10		12	20000		21600	18000	24000	1,2		0,9
Итого:		х	х	х		Х	50000		51600	40500	64000	х		х

1. Индивидуальные индексы физического объема реализации определяются по формуле

Индексы физического объема реализации

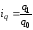
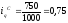или 75,0 % (уменьшение объема продажи на 25%)

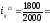0,9 или 90,0% (уменьшение на 10%)

Индексы физического объема цены

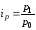
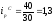или 130,0%

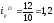или 120,0% (повышение цены соответственно на 30% и 20%)

Основной формой общих индексов являются агрегатные индексы, в которых достигается соизмеримость разнородных показателей, являющихся элементами сложных совокупностей. При этом в числителе и знаменателе общего индекса изменяется только значение индексируемой величины, а их соизмерители являются постоянными величинами и фиксируются на одном уровне базисного или отчетного периода.

Агрегатная формула индекса цен Г. Пааше имеет вид:

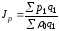
Используя расчетные показатели таблицы, получим 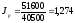или 121,5%, т.е. по двум видам товаров цены повысились в среднем на 27,4%.

Агрегатная формула индекса цен Э. Ласпейреса

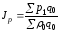, тогда

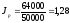или 128,0%, т.е. если бы объем продажи в отчетном периоде по сравнению с базисным не изменился, то цены в среднем увеличились бы на 28,0%.

При вычислении индекса физического объема также возможны разные решения в зависимости от выбора соизмерителя.

По методике Г. Пааше , тогда 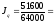0,806 или 80,6%, т.е. физический объем реализации в фактических ценах уменьшился на 19,4%.

По методике Ласпейрес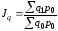а , тогда 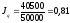или 81% - объем реализации в сопоставимых ценах снизился на 19%.

Общий индекс оборота (стоимости реализации) в текущих ценах 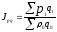, т.е. 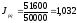или 103,2%, т.е. в отчетном периоде по сравнению с базисным оборотом вырос на 3,2%.

Агрегатные индексы взаимосвязаны между собой по формуле

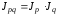(мультипликативная модель).

Эта взаимосвязь возможна в двух вариантах сочетания этих индексов:

индекса физического объема Ласпейреса и индекса цен Пааше

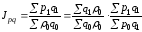
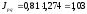
индекса физического объема Пааше и индекса цен Ласпейреса

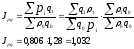
Формулы агрегатных индексов позволяют осуществить разложение абсолютного прироста оборота по факторам:

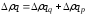(аддитивная модель),

где 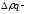абсолютный прирост стоимости продукции всего в том числе:

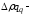вследствие изменения физического объема реализации;

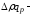вследствие изменения цены;

По методике Пааше:

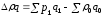
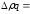51600-50000=1600 р.

в т.ч. а)

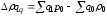
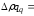40500-50000= -9500 р., т.е. оборот за счет изменения физического объема продажи уменьшился на 9500 р.

б)

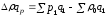
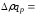51600-40500=11100, т.е. оборот в результате среднего изменения цены увеличился на 11100 р.

проверка:

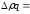-9500+11100=1600

Методика Ласпейреса:

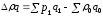
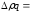51600-50000=1600р.

в т.ч. а)

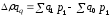
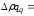51600-64000= -12400 р. т.е. уменьшение оборота в фактических ценах за счет изменения физического объема составило 12400 р.

б)

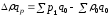
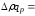64000-50000=14000 р., т.е. условный прирост оборота при сохранении объема продажи на базисном уровне 14000 р.

Проверка:

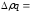- 12400+14000=1600 р.

В экономической практике возникают случаи, когда известны не абсолютные значения индексируемых показателей, а их относительные изменения. Тогда агрегатный индекс можно рассчитать косвенным путем, если известен результативный показатель отчетного или базисного периода, используя индивидуальные индексы.

Задача 2. Имеются данные по производственной фирме

Таблица 11.

Виды продукции	Затраты на производство, тыс. руб.			Изменение физического объема производства в отчетном периоде по сравнению с базисным, %
	Базисный период	Отчетный период
	
А	640	768	-24
Б	400	540	Без изменения
В	160	180	+30

Агрегатный индекс физического объема производства исчисляется по формуле:

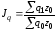
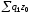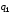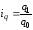
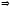
Для определения найдем из формулы индивидуального индекса физического объема: 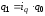, тогда

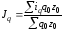, т.е. агрегатный индекс физического объема преобразовали в среднеарифметический индекс.

1) По данным об изменении натурального выпуска продукции (табл.11) определим индивидуальные индексы:

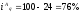или 0,76

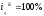или 1

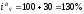или 1,3

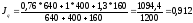или 91,2,% т.е. объем производства в целом снизился на 8,8 %.

Общий индекс затрат на производство продукции 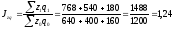или 124 % , т.е. производственные затраты фирмы увеличиличь на 24%.

3) Для определения общего индекса себестоимости используем формулу взаимосвязи

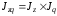, тогда

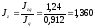или 136,0 % , себестоимость единицы продукции по фирме увеличилась в среднем на 36 %.

Задача 3. Рассмотрим пример решения задачи, информация к которой внесена в табл. 12.

Таблица 12

Вид продукции	Оборот в фактических ценах, тыс. р.			Изменение средних цен во 2 квартале по сравнению с 1, %
	1 квартал	2 квартал
А	120	160	+15
Б	48	60	+6
В	64	90	+3

Определяем индивидуальные индексы цены (данные табл.12)

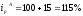или 1,15

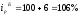или 1,06

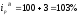или 1,03

Общий индекс цены: 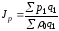, для определения условного оборота определяем 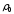из формулы индивидуального индекса цены 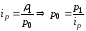, тогда 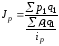, т.е. преобразовали агрегатную формулу в средне гармоническую форму.

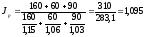или 109,5 % , т.е. цены в отчетном периоде по сравнению с базисным повысились в среднем на 9,5%.

Определим индекс оборота в фактических ценах 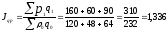или 133,6 % ,т.е. оборот увеличился на 33,6%.

Индекс оборота в сопоставимых ценах (индекс физического объема) можно определить по формуле взаимосвязи: 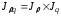, тогда:

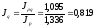или 81,9 % ,т.е. натуральный объем продажи уменьшился на 18,1%.

Сумма денежных средств, дополнительно затраченных населением вследствие повышения цен адекватна приросту оборота в результате повышения цен.

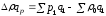
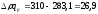тыс. р. – население дополнительно затратило в отчетном периоде на указанные товары 26,9 тыс. р.

Задача 4. Имеются данные о продаже товара А на трех субрынках района:

Таблица 13

Субрынок	Цена за ед., р.		Объем продажи, тыс.ед.		Расчетные показатели
					Стоим. прод. (об.), тыс.р.			Индекс цены	Уд. вес прод.,%
	баз. пер.	отч. пер.	баз. пер.	отч. пер.	баз. пер.	отч. пер.	услов.		баз. пер.	отч. пер.
Усл. обоз.
1	38	40	24	22	912	880	836	1,053
2	34	36	41	39	1394	1404	1326	1,058
3	35	38	39	35	1365	1330	1225	1,086
Итого	-	-	104	96	3671	3614	3387	-

Решение:

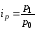
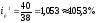
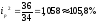
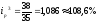, т.е. уровень цены товара А на 1 рынке увеличился на 5,3%, на 2 – повысился на 5,8%, на 3 - повысился на 8,6%.

2. а)

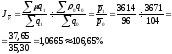
Средняя по трем рынкам цена повысилась примерно на 6,7%.

б)

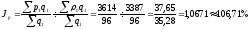
или

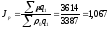
За счет изменения цены на каждом рынке средняя цена повысилась на 6,7%

в)

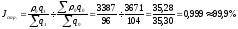
или

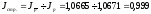
За счет изменения структуры продажи по рынкам (см. таблицу структурные сдвиги незначительны) средняя цена снизилась на 0,1%.

3. Тоже в абсолютном выражении:

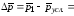37,65-35,30=2,35 р.

а) 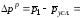37,65-35,28=2,37 р.

б) 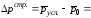35,28-35,30= - 0,02 р.

Проверка:

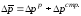
2,35=2,37-0,02=2,35 р.

Повышение средней цены ед. товара А составило 2,37 р., в т.ч. за счет изменения цены на каждом рынке на 2,35 р., за счет изменения доли продажи по рынкам средняя снизилась на 0,02 р.