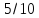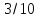Контрольная работа по теории вероятности

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Уральский государственный экономический университет» в г. Березники

Кафедра экономики

Контрольная работа

по дисциплине: «Теория вероятностей»

Вариант №2

Выполнил:

студент 1 курса, группы БЭС-12

Григорьев М.А.

Проверил:

К.ф.-м.н., профессор

Кобзев Виктор Николаевич

Березники

2013

Вариант №2

Задание №1

В первой урне находятся 17 белых и 3 черных шаров, во второй урне – 4 белых и 4 черных шаров. Из первой урны во вторую переложили 2 шара, а затем из второй урны извлекли один шар.

Найти вероятность того что этот шар белый.

Решение:

Мы провели 3 опыта:

1. Из 1-ой урны во 2-ую переложили 1 шар

2. Из 1-ой урны во 2-ую переложили 1 шар

3. Из 2-ой урны извлекли 1 шар

Следовательно, дерево вероятностей содержит 3 уровня вершин и 2 возможных варианта исхода. Составим дерево вероятностей.

Достаем 1-ый шар из 1-ой урны
Белый						Черный
2-ой шар из 1-ой урны						2-ой шар из 1-ой урны
Белый			Черный			Белый			Черный
Шар из 2 урны			Шар из 2 урны			Шар из 2 урны			Шар из 2 урны
Белый	Черный	Белый		Черный	Белый		Черный	Белый		Черный
Б Б Б	Б Б Ч	Б Ч Б		Б Ч Ч	Ч Б Б		Ч Б Ч	Ч Ч Б		Ч Ч Ч

Всего 8 возможных путей, выбираем вероятности при которых шар извлеченный из 2 урны шар будет белым.

Вероятность того что шар извлеченный из 2 урны будет белый равна:

Задание №2

На заводах A и B изготавливают 90% и 10% всех деталей. Из прошлых данных известно, что 30% деталей завода А и 10% деталей завода В оказываются бракованными. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она изготовлена на заводе А?

Решение:

Проводим 2 опыта:

1. Случайно выбираем завод

2. Случайно выбираем деталь

Составим дерево вероятностей.

Выбран завод
А		В
Брак	Не брак		Брак	Не брак

Найдем процент брака на заводах А и В:

Найдем процент брака на заводе А:

Вероятность того, что бракованную деталь изготовили на заводе А будет равна:

Задание №3

Вероятность поражения стрелком мишени при одном выстреле равна . Найти вероятность того что при выстрелах мишень будет поражена не менее раз.

Решение:

Найдем вероятность поражения стрелком мишени используя интегральную теорему Лапласа.

=

Задание №4

Среднее число самолетов, прибывающих в аэропорт за 1 минуту, равно . Найти вероятность того, что за время минуты прибудут:

1. самолетов

2. не менее самолетов

Поток предполагается простейшим.

Решение:

1. 

2. События и

противоположные.

Поэтому сумма их вероятностей равна 1.

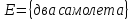
Тогда,

Задание №5

Произведено независимых испытаний. В каждом из них вероятность появления события А равна . Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа .

Решение:

Где Ф функция Лапласа.

Задание №6

Дискретная случайная величина принимает значения с вероятностями .

Найти ее математическое ожидание и дисперсию.

Решение:

Для определения математического ожидания и дисперсии дискретной СВ Х заполним таблицу.

4	0,4	1,6	16	6,4
7	0,5	3,5	49	24,5
1	0,1	0,1	1	0,1
Сумма	1	5,2	66	31

1. 

2. 

Задание №7

Плотность распределения вероятностей непрерывной случайной величины Х имеет вид, показанный на графике. Найти неизвестное число m, функцию распределения F(x), математическое ожидание М(х) и дисперсию D(x).

Решение:

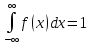свойство функции f(x)

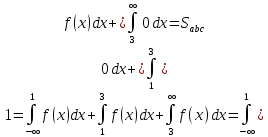
(геометрический смысл определенного интеграла)

На участке 1 и на участке 4

На участке 2 это отрезок прямой AB. Проходящей через точки , тогда

Следовательно

На участке 3 график f(x) это отрезок прямой СВ. Проходящей через точки , тогда

Следовательно

Найдем функцию распределения F(x). Известно, что

Воспользуемся геометрическим смыслом определенного интеграла.

Если , то и площадь под кривой равна 0.

Если , то

Если , то

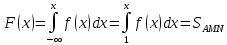
Координаты точек М(х;0) и N(х;f(х)). Тогда

Если , то

Координаты точек

Тогда

Математическое ожидание:

Дисперсия:

Задание №8

Плотность распределения вероятностей нормально распределенной случайной величины Х имеет вид

Найти неизвестно число , математическое ожидание M(X), дисперсию D(X),

вероятность выполнения неравенства и .

Решение:

Выделим полный квадрат в выражении:

Следовательно, из нормального закона распределения вероятностей:

Следовательно

1. 

2. 

3. 

4. и

Это стандартное отклонение.