математика .xlsx

Задача1. Вариант 6.

По координатам вершин треугольника А (0;0); В (8;2); С (-2;6) найти:

1) периметр треугольника; 2) уравнение сторон треугольника;

а) Для нахождения сторон периметра Р применим формулу:

Р=АВ+ВС+АС

Длины сторон найдём по формуле расстояния между двумя точками:

d=

АВ==

ВС==

АС=

P_ABC=+

б) Для отыскания уравнений сторон треугольника используем уравнение прямой, проходящей через две данные точки М1(х₁у₁) и М2(х₂у₂): =

АВ: А(х₁у₁) В(х₂у₂):=

ВС: А(х₁у₁) В(х₂у₂):=

Ответ: а) P_ABC=+ ; б) АВ: ; ВС:.

Задача2. Вариант 6.

Найти первую производную функцию:

Решение: Для решения и нахождения производных используется данная формула

Задача3. Вариант 6.

Вычислить площадь плоской фигуры, ограниченной заданными координатами. Сделать чертёж.

Решение: Если кривая имеет уравнение у= то площадь, ограничения этой кривой и отрезком [], принадлижащим оси О, вычисляется по формуле

х	0	-1
у	1	2

Найдём точки пересечения параболы и прямой: . Таким образом, заданные кривые пересекаются в точках В(0;1) и А (-1;2).Площадь заштрихованной фигуры можно найти как разность площадей треугольника ОАВ и фигуры, ограниченной кривой , осью О и прямой АВ.

Следовательно, .

Задача 4. Вариант 6.

Найти линейные комбинации заданных матриц: A = ,

Найти: 2B-A

A =,

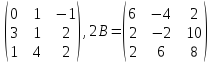2B-A=.

Ответ: 2B-A=

Задача 5. Вариант 6.

Решить систему уравнений:

Решение:

Решим систему уравнений методом Крамера. Найдём определители.

При вычислении определителя 3-го порядка используя правило Саррюса

которое символически можно записать так:

Ответ:

Задача 4. Вариант 6.

Банк даёт своим вкладчика 7%годовых. Чему станет равен вклад в 400000 рублей через 3 года.

Найдём сколько рублей начислил банк за первый год:

1) 400000 0,7 = 28000. 2) 400000 + 28000 = 428000 - сумма вклада через год.

3) 428000 0,7 = 29960 - деньги начслены за 2-й год. 4) 428000 + 29960 = 457960 - сумма вклада на 2-й год. 5) 457960 0,7 = 32507,2 - деньги начслены за 3-й год.

6) 457960 + 32507,2 = 490469,2 - деньги начислены за 3-й год. Ответ: Через 3 года вклад будит равен 490469,2 рублей.