
математика
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «Уральский государственный экономический университет»
Центр дистанционного образования
Контрольная работа
по дисциплине: Математика.
Исполнитель: студент
Направление: Государственное и муниципальное управление
Группа: ГМУ-13Р
Ф.И.О: Кустов Александр Сергеевич
Екатеринбург
2014 г.
Тема 1. Матрицы и определители.
1.1. Вычислить определитель.
4.



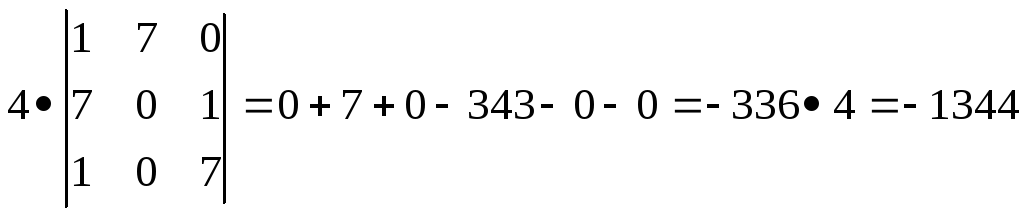

![]()
1.2. Найти обратную матрицу для матрицы А и сделать проверку.
4.




 - матрица
миноров соответствующих элементов
матрицы А.
- матрица
миноров соответствующих элементов
матрицы А.
![]()
![]()

Проверка:
 =Е
=Е
Тема 2. Системы линейных уравнений.
4. Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.






![]()
![]()
![]()
Тема 3-4. Векторная алгебра. Уравнение прямой.
4. По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.
А(3; 1); В (3; –5); С(–1; –1).


Тема 4. Уравнение плоскости.
4. Даны точки М1 и М2.
Составить
уравнение плоскости, проходящей через
точку ш1
перпендикулярно вектору
![]()
Найти отрезки, отсекаемые данной плоскостью на осях координат.
М1 (–2; 3; 1); М2 (1; 1; 4).
Пусть
![]() точка
пересечения вектора
точка
пересечения вектора
![]() и плоскости.
и плоскости.

Если
![]() ,
то уравнение может быть записано в виде
уравнения плоскости в отрезках.
,
то уравнение может быть записано в виде
уравнения плоскости в отрезках.

![]() - отрезки, отсекаемые
данной плоскостью на осях координат.
- отрезки, отсекаемые
данной плоскостью на осях координат.
Тема 5. Линии второго порядка
4. Найти координаты вершин оси, фокусы и эксцентриситет эллипса. Сделать чертеж.
![]()
При
![]()
![]() ,
,
![]()
При
![]()
![]() ,
,
![]()
![]() - координаты вершин эллипса.
- координаты вершин эллипса.
![]() ,
,
![]()

![]()
![]() – фокусы эллипса
– фокусы эллипса
![]() – эксцентриситет
эллипса
– эксцентриситет
эллипса

Тема 6. Пределы функций
4. Вычислить пределы
![]()
![]()

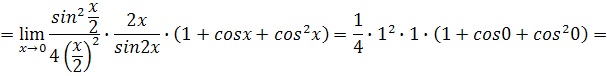
![]()
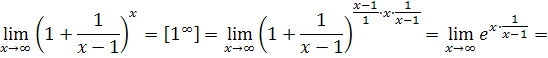
![]()
Тема 7. Основы дифференцирования
4. Найти производную
сложной функции ![]()
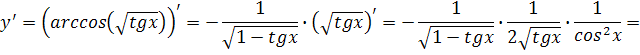

Тема 8. Исследование функции
4. Исследовать
функцию и построить её график ![]()
1)
![]() .
.
2)
![]() ,
,
![]() ,
,
![]() ,
таким образом функция не является чётной
и не является не чётной.
,
таким образом функция не является чётной
и не является не чётной.
3) Функция не периодическая.
4) Вертикальных асимптот нет.
5) Пересечения с осями координат:
OY:
х=0, ![]()
OX:
y=0,
![]() ,
,
![]()
![]() x
x![]()
x=-1
![]() - точка пересечения с осью ОУ
- точка пересечения с осью ОУ
(-1;0), (0;0) – точки пересечения с осью ОХ.
6) Промежутки убывания и возрастания графика функции
|
+ |
- |
+ |
|
-1 |
0 |
|
![]() при
при ![]()
![]() при
при
![]()
7) Экстремумы функции:
![]()
![]() ,
,
![]()
![]()
|
x |
|
|
|
|
y’ |
- |
0 |
+ |
|
y |
убывает |
|
возрастает |
![]() - точка минимума
- точка минимума
8) Выпуклость и вогнутость функции
![]()
![]() ,
,
![]() ,
точек перегиба нет
,
точек перегиба нет
9) Построение графика функции

Тема 9. Неопределенный интеграл
Вычислить неопределенный интеграл






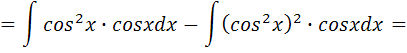

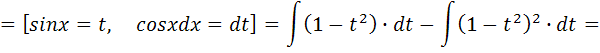

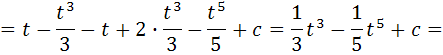




Тема 10. Определенный интеграл
Вычислить определенный интеграл









Запишем начало и конец равенства:



Вычислить площадь фигуры, ограниченной кривыми. Сделать чертеж



Тема 11. Несобственный интеграл
Вычислить интеграл или установить его расходимость


![]() =
=![]()


Тема 12. Ряды
Числовые ряды. Исследовать ряд на сходимость



Ряд сходится.
Степенные ряды. Определить область сходимости степенного ряда


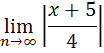
Ряд абсолютно
сходится для x:
![]()
![]()
![]()
![]()
![]() – область
сходимости
– область
сходимости
Тема 13. Функция нескольких переменных
Исследовать функцию на экстремум

Найдем производные первого порядка:

Найдем стационарные точки:

Найдем частные производные второго порядка:
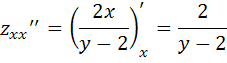
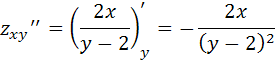

В точке экстремума
![]() частные производные второго порядка
примут вид:
частные производные второго порядка
примут вид:

Проведем дополнительное исследование:
![]() рассмотрим
функцию z(x,y)
в окрестности
точки А.
рассмотрим
функцию z(x,y)
в окрестности
точки А.

![]()
![]()
![]()
![]()
Тема 14. Решение дифференциальных уравнений
Найти общее и частное решение ДУ
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()


![]()
![]() - общее
решение ДУ
- общее
решение ДУ
![]()
![]()



![]() - частное
решение ДУ
- частное
решение ДУ
Найти общее решение ДУ
![]()
Пусть ![]()
![]()
Пусть ![]()
![]()
![]()
Пусть ![]()
![]()

![]()
![]()
![]()
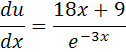









![]()
![]()
![]()
![]()
![]()
![]()



![]() - общее решение ДУ
- общее решение ДУ
Тесты для промежуточного контроля знаний.
1. Разложение
по первой строке определителя
 имеет вид:
имеет вид:
-
a11 + 2a12 – a13; б) 3a12; в) –a11 + 3a12; г) a11 + a12 + a13.
2. Даны матрицы
![]() и
и
![]() Тогда А – B
равно:
Тогда А – B
равно:
-
 б)
б)
 в)
в)
 г)
г)

3. Матрица![]() не имеет
обратной при
λ, равном:
не имеет
обратной при
λ, равном:
а) –1; б) 0; в) –2; г) 1.
4. Система
линейных уравнений с основной матрицей
 и вектором правых частей
и вектором правых частей
 имеет вид:
имеет вид:
а)
 б)
б)
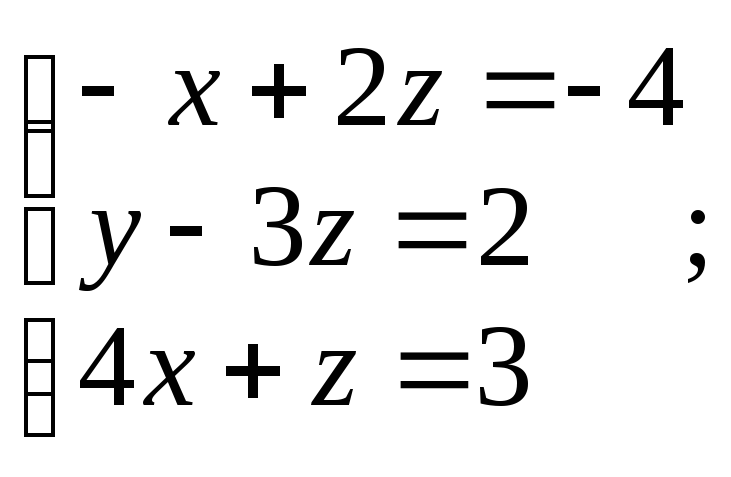
в)
 г)
г)
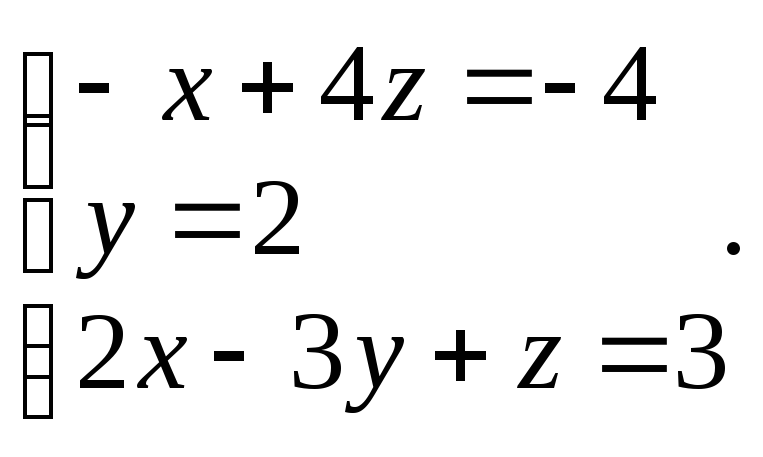
5. Длина отрезка, отсекаемого прямой 2x + 4y – 8 = 0 на оси Ox, равна:
а) 3; б) 5; в) 4; г) 8.
6. Найдите уравнение прямой, перпендикулярной прямой y = –4x + 1:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
7. Координата x0 точки A(x0, 5, 10) принадлежащей плоскости 2x – y + z – 10 = 0, равна:
а) –2; б) 0; в) 2,5; г) 1.
8. Значение
предела
![]() равно:
равно:
а) 0; б) 5/3; в) 1; г) 3/5.
9. Закон движения материальной точки имеет вид x(t) = t3 – 4t, где x(t) – координата точки в момент времени t. Тогда скорость точки при t = 2 равна …
а) 24; б) 8; в) 18; г) 20.
10. На рисунке изображен график производной функции y = f(x), заданной на отрезке [–1; 8].

Тогда точкой максимума этой функции является:
а) 8; б) 0; в) 3; г) –1.
11. Множество первообразных функции f(x) = sin3x имеет вид:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
12. Вектор
![]() перпендикулярен вектору
перпендикулярен вектору
![]() ,
если λ равно:
,
если λ равно:
а) 1; б) –2; в) –1; г) 2.
13. Векторы
![]() и
и
![]() коллинеарны, если k
равно:
коллинеарны, если k
равно:
а) 1; б) –2; в) –10; г) 4.
14. Если
![]() и
и
![]() ,
тогда скалярное произведение
,
тогда скалярное произведение
![]() равно:
равно:
a) 5; б) 10; в) 7; г) 12.
15. Модуль комплексного числа 1 + i равен:
a)
![]() б) 4; в) 7; г) 3.
б) 4; в) 7; г) 3.
16. Если
z
= 5 – 2i,
то сопряженное ему комплексное число
![]() равно:
равно:
a) 5 + 2i; б) –5 – 2i; в) 5i – 2; г) –5+2i.
17. Действительная часть комплексного числа (1 – i)2 равна:
a) 2; б) –1; в) 0; г) 1.
18. Значение функции f(z) = 3z – 1 в точке z0 = 1 + 2i равно:
a) –2 + 6i; б) 2 + 6i; в) –1 + 4i; г) –2 + 5i.
19. Периодической является функция:
a) f(x) = x + x2; б) f(x) = sin(x + π); в) f(x) = lnx; г) f(x) = 5π.
20. Для периодической функции f(x) с периодом T = 3, при всех x из области определения, выполняется равенство:
a) f(x + 3) = f(x); б) f(x – 3) = f(x);
в) f(3x) = f(x); г) f(x/3) = f(x).
21. Если
![]() то числовой ряд сходится при l,
равном:
то числовой ряд сходится при l,
равном:
a) 0,5; б) 1; в) –2; г) 2.
22. Общий интеграл
дифференциального уравнения
![]() имеет вид:
имеет вид:
a)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
23. Дано
дифференциальное уравнение
![]() тогда функция y
= x4
является его решением при λ,
равном:
тогда функция y
= x4
является его решением при λ,
равном:
a) 2; б) 1; в) 3; г) 0.
24. Дано
дифференциальное уравнение
![]() Тогда соответствующее ему характеристическое
уравнение имеет вид:
Тогда соответствующее ему характеристическое
уравнение имеет вид:
a)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()


