Детерминированные модели управления запасами.

1.Детерминированная обобщённая модель определения оптимального размера партии продукции при допущении дефицита.

Рассматривается система управления запасами, когда продукция поступает на склад непосредственно с производственной линии с постоянной интенсивностью единиц продукции в единицу времени. При достижении некоторого уровня объёма запаса Q производство продукции прекращается. Возобновление производства и поставки продукции на склад осуществляется в момент, когда неудовлетворённый спрос достигнет некоторого значения G. Расходование запаса осуществляется с интенсивностью . Известны значения следующих параметров:- стоимость хранения единицы товара на складе в единицу времени;-стоимость организации заказа (одной партии продукции);- убытки от неудовлетворенного спроса (штраф). Требуется найти оптимальный объём партии продукции и интервал времени между точками возобновления поставки по критерию минимума общих затрат от функционирования системы управления запасами.

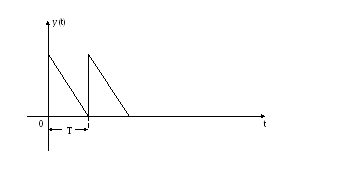
Графически условия задачи показаны на рис.3.

Из рисунка видно, что пополнение и расходование запаса осуществляются одновременно в течение интервала каждого цикла. Накопленный запасQ полностью расходуется в течение интервала . В течение интерваласпрос не удовлетворяется, а накапливается. Неудовлетворённый спросG покрывается в интервале . Величинаназываетсяполным циклом управления запасом. - предельный запас продукции,G – предельный дефицит продукции.

Очевидно текущий уровень запаса продукции определяется по формуле:

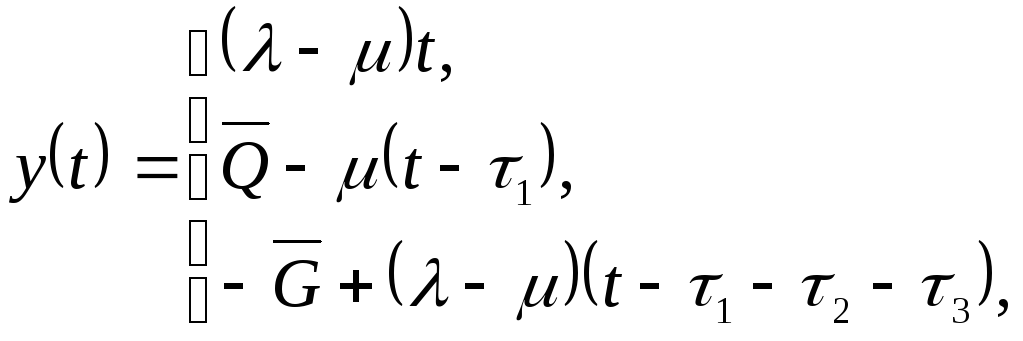
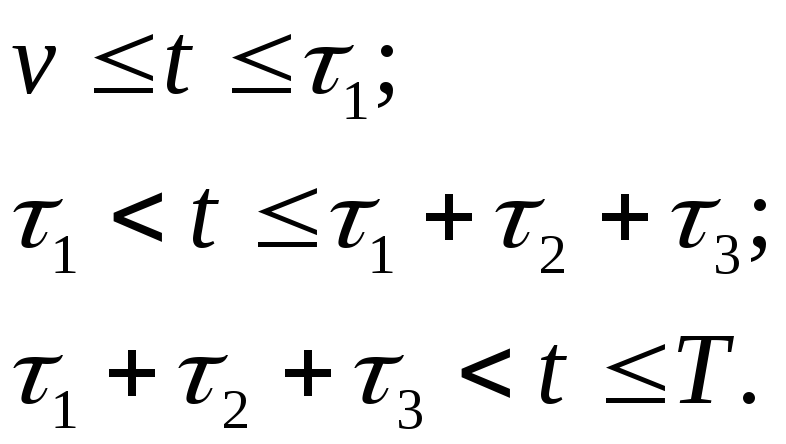
Из треугольника OAB следует:

или . (1)

Аналогично можно определить ,и(2)

Из подобия треугольников OAC и CEF можно записать Из равенства следует, что(3)

Выражение (3) с учётом (1) перепишется:

(4)

Тогда общая сумма затрат на пополнение, хранение запаса продукции и возможный штраф за неудовлетворительный спрос будет определяться выражением:

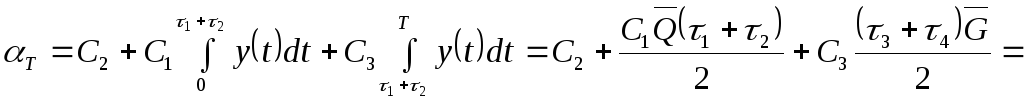
Если привести затраты в единицу времени, то выражение для удельных затрат будет иметь вид:

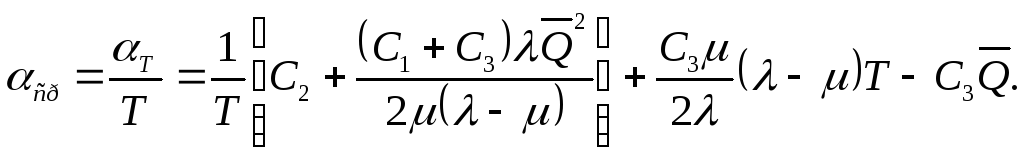
Таким образом, есть функция двух аргументовQ и T, оптимальные значения которых определяются как решение задачи:

Для того, чтобы найти минимум функции двух аргументов, необходимо и достаточно решить систему уравнений:

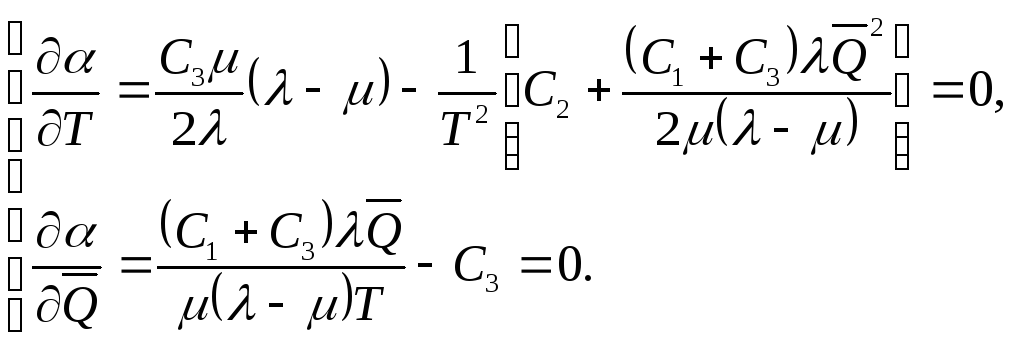(5)

Это следует из факта, что функция является вогнутой функцией относительно своих аргументов. Решение системы уравнений (5) даёт следующие неотрицательные корни:

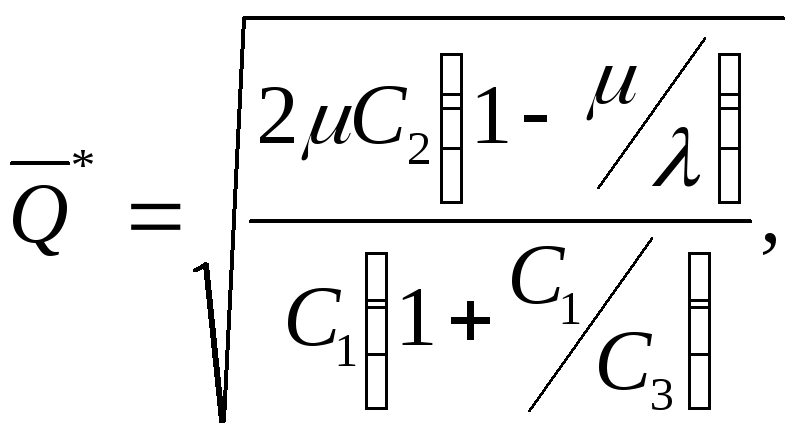(6)

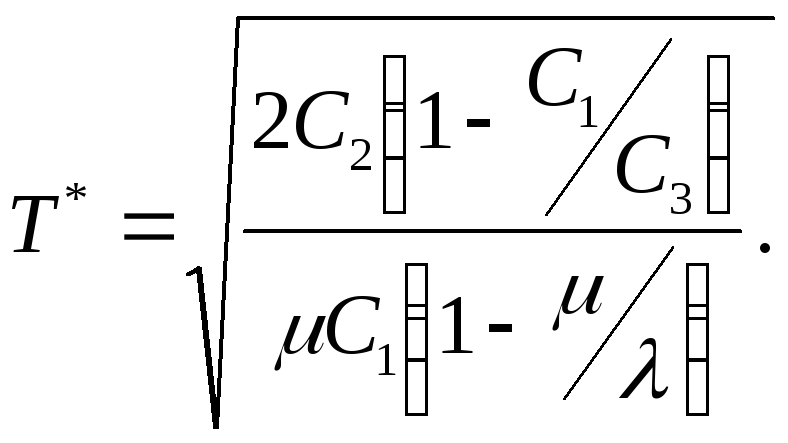(7)

Минимум общих затрат в единицу времени составит:

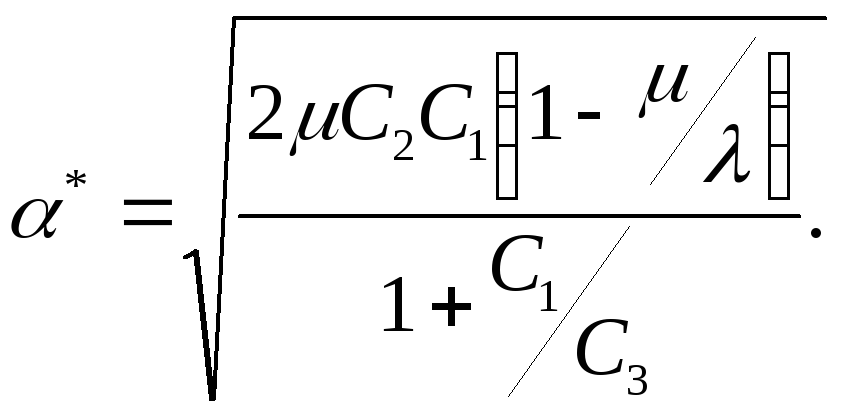(8)

Можно рассмотреть частные случаи.

1. Дефицит продукции не допускается. Решение задачи в этом случае получается из формулы (6)-(8), если положить штраф 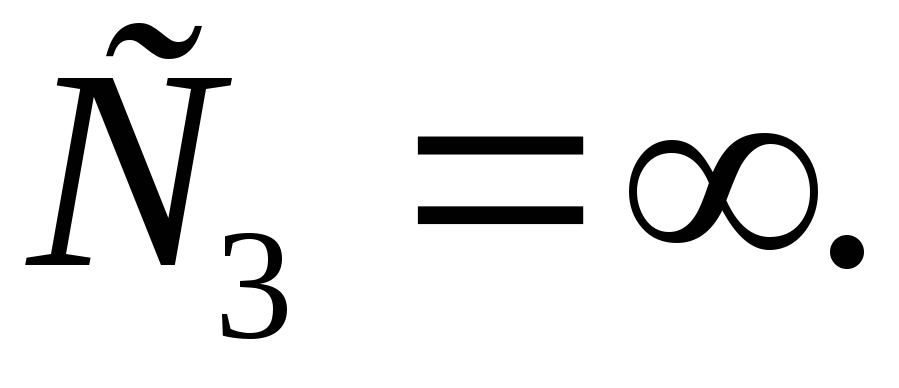Тогда С₁/С₃=0 и оптимальные значения искомых величин будут:

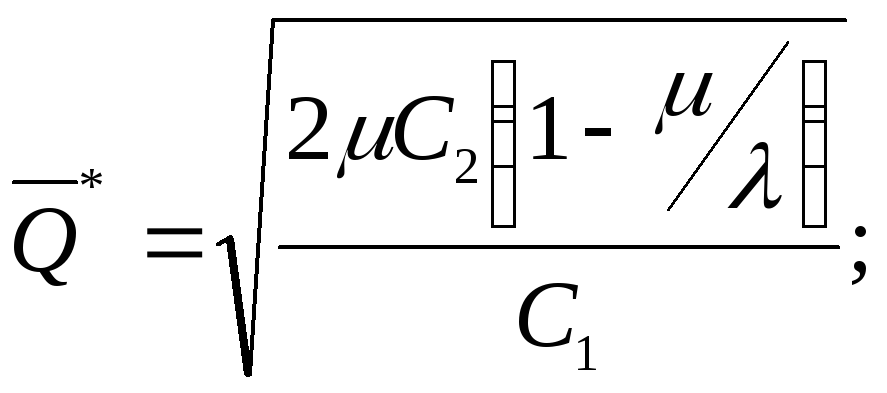
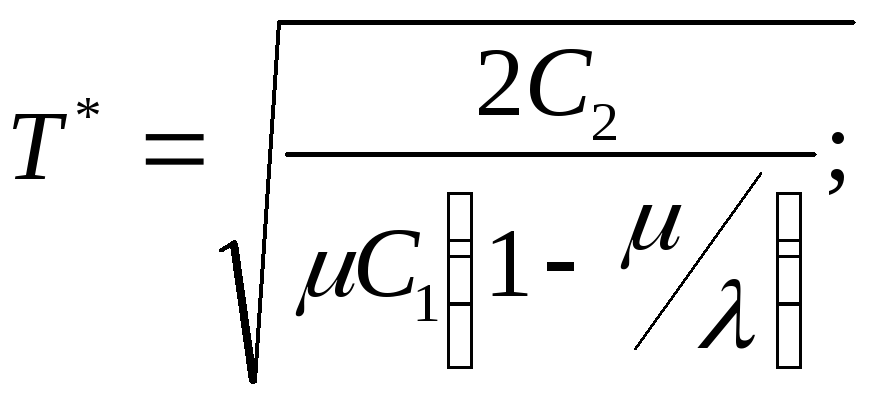
Этому случаю соответствует график изменения уровня запаса во времени:

2. Пополнение запаса осуществляется мгновенно. В этом случае полагается 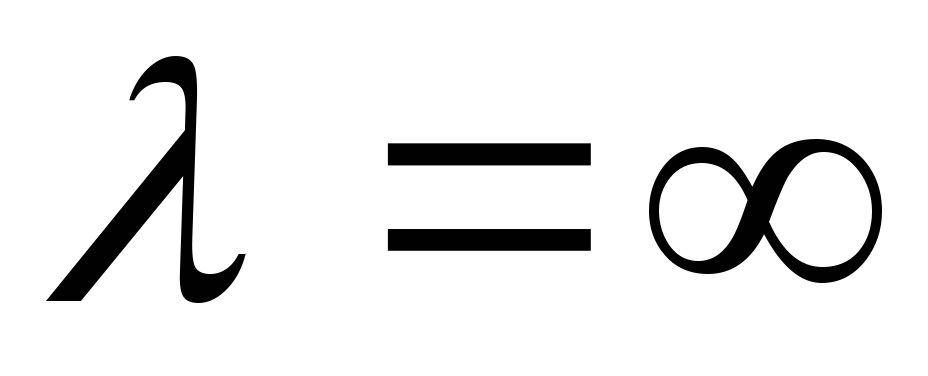и соответственно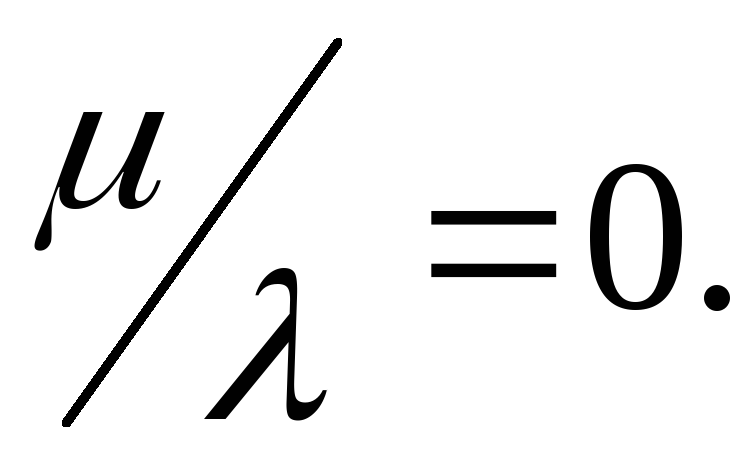

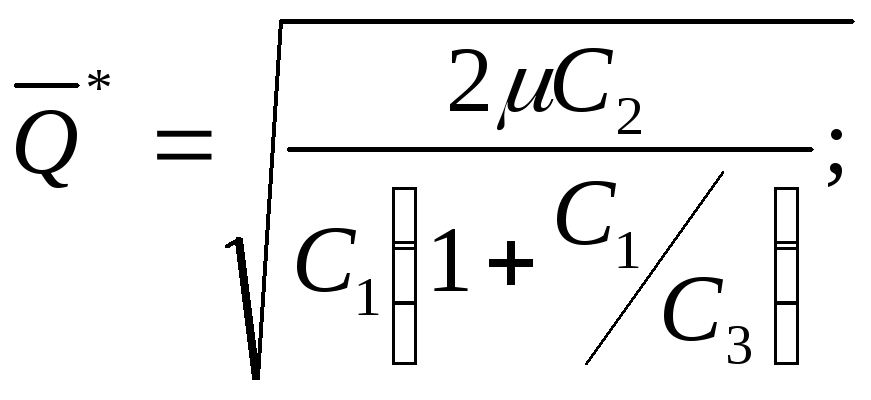
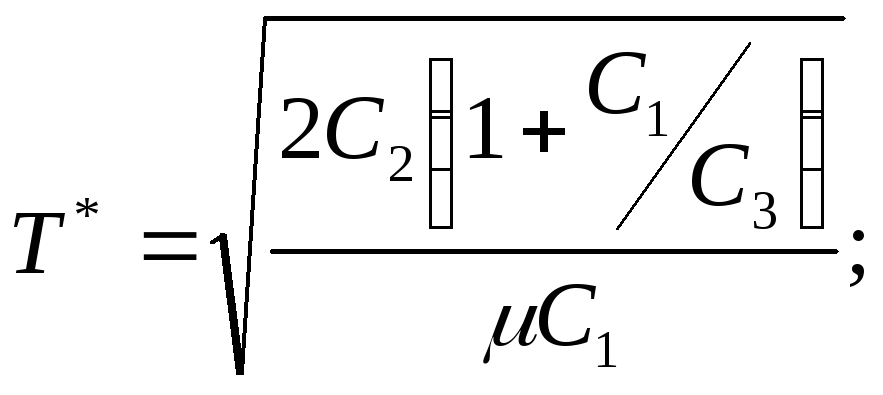
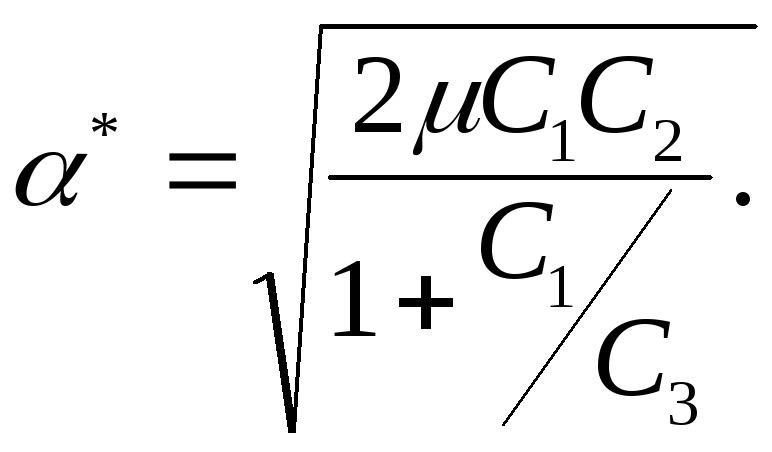
График изменения уровня запаса имеет вид:

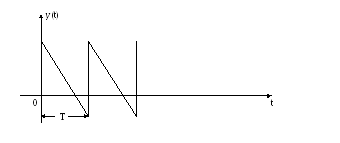
3. Дефицит не допускается, запасы пополняются мгновенно, т.е. 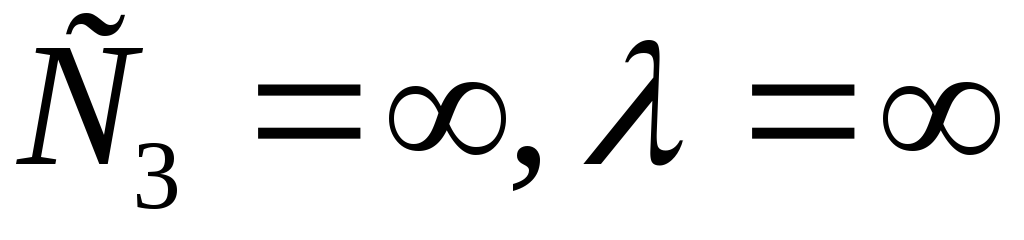. Тогда следует:

Эти формулы называются формулами Уилсона, а величина - экономическим размером партии.

График изменение уровня запаса имеет вид: