
- •Математика
- •Методические указания по самостоятельной работе студентов
- •I. Введение
- •II. Игры с нулевой суммой
- •Тема 1. Выбор стратегии
- •Тема 2. Решение игр в смешанных стратегиях
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •III. Игры с ненулевой суммой
- •Тема 3. Понятие точек равновесия
- •Точка равновесия по Нэшу
- •IV. Игры с природой
- •Тема 4. Игры с природой
- •Стохастическая задача Критерий Байеса (Лапласа).
- •Нестохастическая задача
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •Тема 3. Понятие точек равновесия
- •Тема 4. Игры с природой
- •Примерные варианты контрольных работ
- •Задания для самостоятельной работы (с ответами)
Тема 2. Решение игр в смешанных стратегиях
Смешанной
стратегией ![]() игрока
игрока
![]() называется применение чистых стратегий
называется применение чистых стратегий
![]() с вероятностями
с вероятностями ![]() причем
причем

Смешанные
стратегии игрока ![]() записываются
в виде матрицы
записываются
в виде матрицы
 или
или
![]() .
.
Аналогично
смешанные стратегии игрока ![]() обозначаются
обозначаются
 или
или![]()
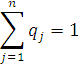
Чистые стратегии можно считать частным случаем смешанных стратегий. Их можно задавать строкой, в которой 1 соответствует активной чистой стратегии, остальные элементы строки равны 0.
На
основании принципа минимакса определяется
оптимальное
решение (или
решение)
игры: это пара оптимальных стратегий
![]() и
и ![]() обладающих следующим свойством: если
один из игроков придерживается своей
оптимальной стратегии, то другому не
выгодно отступать от своей.
обладающих следующим свойством: если
один из игроков придерживается своей
оптимальной стратегии, то другому не
выгодно отступать от своей.
Выигрыш, соответствующий оптимальному решению, называется ценой игры v.
![]() ,
где
,
где
![]() – нижняя и верхняя цены игры.
– нижняя и верхняя цены игры.
Теорема Неймана (основная теорема теории игр).
Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.
Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.
Теорема. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий (теорема позволяет строить модели нахождения оптимальных стратегий при отсутствии седловой точки).
Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
Простейший случай конечной игры.
Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке.
Если седловой точки нет, воспользуемся теоремой об активных стратегиях.
Если
игрок I
придерживается
своей оптимальной стратегии ![]() ,
то его средний выигрыш будет равен цене
игры v,
какой бы активной стратегией ни
пользовался игрок II.
Для игры 2 × 2 любая чистая стратегия
противника является активной, если
отсутствует седловая точка. Поэтому
средний выигрыш игрока I(оптимальная
стратегия) будет равен v
и для 1-й, и для 2-й стратегии противника.
,
то его средний выигрыш будет равен цене
игры v,
какой бы активной стратегией ни
пользовался игрок II.
Для игры 2 × 2 любая чистая стратегия
противника является активной, если
отсутствует седловая точка. Поэтому
средний выигрыш игрока I(оптимальная
стратегия) будет равен v
и для 1-й, и для 2-й стратегии противника.
Выигрыш игрока I (проигрыш игрока II) – случайная величина, математическое ожидание которой является ценой игры.
Пусть
игра задана платежной матрицей ![]() .
.
Средний
выигрыш игрока I,
если он использует оптимальную смешанную
стратегию ![]() а игрок II
– чистую
стратегию
а игрок II
– чистую
стратегию ![]() ,
равен цене игры v.
,
равен цене игры v.
![]()
Если
игрок II
использует
чистую стратегию ![]() ,
то для игрока I
получаем
,
то для игрока I
получаем
![]()
В итоге имеем систему уравнений

Решая эту систему, получим оптимальную стратегию
![]()
![]()
и цену игры
![]()
Аналогично находится оптимальная стратегия II игрока:
![]()
![]()
Пример 3. Найти оптимальные стратегии игры «Орлянка».
Игра
задана платежной матрицей ![]()
![]() ,
,
![]() седловой точки нет.
седловой точки нет.
Ищем решение в смешанных стратегиях.
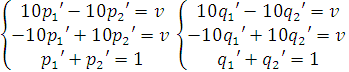
Решая эти системы, получаем
![]()
![]()
Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы выбирать «Орел» или «Решка» с вероятностью 0,5, при этом средний выигрыш будет равен 0.
Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
Рассмотрим
игру заданную матрицей выигрышей размера
![]()
У
игрока I
есть две стратегии ![]()
Для графического решения используем ортогональную декартову систему координат X0Y.
По
оси абсцисс от точки 0 отложим единичный
отрезок ![]() ,
,
точка
![]() (
(![]() )
соответствует стратегии
)
соответствует стратегии ![]() (1-ой стратегии игрока I),
(1-ой стратегии игрока I),
точка
![]() (
(![]() )
соответствует стратегии
)
соответствует стратегии ![]() (2-ой стратегии игрока I).
(2-ой стратегии игрока I).
Все
промежуточные точки отрезка ![]() –
смешанные стратегии
–
смешанные стратегии ![]() игрока I.
игрока I.
Отрезок
![]() это вероятность
это вероятность ![]() стратегии
стратегии ![]() ,
,
отрезок
![]() это вероятность
это вероятность ![]() стратегии
стратегии ![]() .
.
Когда
смешанная стратегия ![]() совпадает с чистой стратегией
совпадает с чистой стратегией ![]() вероятность
вероятность ![]() ,
и наоборот,
,
и наоборот,
когда
смешанная стратегия ![]() совпадает с чистой стратегией
совпадает с чистой стратегией ![]() вероятность
вероятность ![]() .
.



На
оси ординат 0Y
откладываем выигрыши игрока I
при стратегии ![]() и
различных стратегиях игрока II,
отмечая их точками
и
различных стратегиях игрока II,
отмечая их точками ![]()
На
прямой, проходящей через точку ![]() параллельно оси 0Y,
откладываем выигрыши игрока I
при стратегии
параллельно оси 0Y,
откладываем выигрыши игрока I
при стратегии ![]() и
различных стратегиях игрока II,
отмечая их точками
и
различных стратегиях игрока II,
отмечая их точками ![]()
Строим
прямые ![]() ‘
для
‘
для ![]() .
.
Ординаты
точек лежащих на прямой ![]() ‘
равны среднему выигрышу игрока I,
когда игрок II
использует i-ую
стратегию, и могут быть вычислены по
формуле математического ожидания
‘
равны среднему выигрышу игрока I,
когда игрок II
использует i-ую
стратегию, и могут быть вычислены по
формуле математического ожидания ![]() для соответствующих смешанных стратегий.
для соответствующих смешанных стратегий.
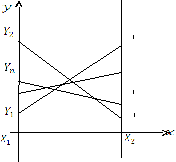
В
соответствии с принципом минимакса
оптимальная стратегия ![]() ‘
такова, что минимальный выигрыш игрока
I
(при наихудшем поведении игрока II)
обращается в максимум.
‘
такова, что минимальный выигрыш игрока
I
(при наихудшем поведении игрока II)
обращается в максимум.



Выделяем нижнюю огибающую графика (ломанную) и определяем на ней точку с максимальной ординатой (ценой игры).
Ей соответствует оптимальная смешанная стратегия игрока I.
Т.к. графическое решение дает не точные результаты определяем прямые на пересечении которых лежит эта точка и решаем систему уравнений.
Определяем цену игры и оптимальные стратегии.
Аналогично
решается игра заданная матрицей выигрышей
![]() .
.
Только в этом случае выделяют верхнюю огибающую графика и на ней ищут точку с минимальной ординатой.
Пример
4.
Решить задачу заданную матрицей платежей
![]()
Решение.
Проверяем матрицу на наличие седловых точек:
![]() ,
,
![]()
![]() седловой
точки нет,
седловой
точки нет, ![]() .
.
Р
Прямые
(1), (2) и (3) соответствуют Строим
нижнюю огибающую. Точка
максимума лежит на пересечении (1) и (2)
прямой. Следовательно,
активными будут только две стратегии
![]() стратегиям
игрока II.
стратегиям
игрока II.
![]() игрока II.
игрока II.






Получили
игру ![]() с матрицей
с матрицей ![]() ,
которая решается аналитически.
,
которая решается аналитически.

![]() ,
,
![]()
Для игрока II получим
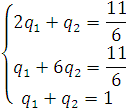
Следовательно,
![]() ,
,
![]()
Ответ:
![]() ‘
‘![]()
