3.12.2 Мінімізація пф із використанням діаграм Вейча (карт Карно)

Діаграми Вейча (карти Карно) [3,11,18] побудовані так, що їхні сусідні клітини відображають члени початкової ПФ, які відрізняються значенням однієї змінної: один член містить цю змінну в прямій формі, а інший - у інверсній. Завдяки цьому виникає наочне уявлення про різноманітні варіанти склеювання суміжних членів.

3.12.2.1 Мінімізація пф за допомогою діаграм Вейча

Початковим продуктом для застосування діаграм Вейча є представлення ПФ таблицею істинності, в якій можливі набори змінних упорядковані за зростанням або за зменшенням їхніх десяткових еквівалентів (таблиця 3.1). Вигляд діаграм Вейча залежить від кількості змінних ПФ - n і від того, як упорядковані набори змінних у таблиці. Якщо набори упорядковані за зростанням їхніх десяткових еквівалентів, то діаграми Вейча для n=2, 3, 4 мають вигляд, наведений на рисунку 3.1.

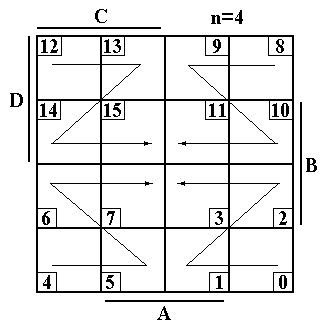
Рисунок 3.1

Кількість клітин діаграми дорівнює кількості наборів змінних

N_кл = N_наб = 2ⁿ . (3.8)

Якщо n = 2, то N_кл = 2² = 4; n = 3, N_кл = 8; n = 4, N_кл = 16.

Кожна клітина відповідає окремому набору змінних і має номер, однаковий із номером набору.

Рядки і стовпці діаграми, що помічені рискою, визначають набори, у які ці змінні входять у прямій формі. Набори, що відповідають іншим рядкам і стовпцям, містять ті ж змінні в інверсній формі. Наприклад, для n = 3 (рисунок 3.1) двом лівим стовпцям відповідає значення змінної В в прямій формі (В), а двом правим - у інверсній ().

В клітини записуються значення ПФ на відповідному наборі (нульове або одиничне). Якщо на якомусь наборі функція не визначена, то в клітині діаграми ставиться риска.

ПФ вважається невизначеною, якщо:

1) існуючий набір змінних у реальному логічному

пристрої неможливий;

2) значення функції на даному наборі байдуже.

Після заповнення діаграми можна приступити безпосередньо до мінімізації, що роблять по одиницям або нулям.

У першому випадку результатом мінімізації буде булевий вираз в ДНФ, а в другому - у КНФ.

3.12.2.1.1 Загальне правило мінімізації

1) Суміжні одиниці (нулі) діаграми умовно охоплюють (накривають) прямокутними контурами. Кожний контур може містити 2,4,8,16, ... одиниць (нулів).

2) Одним контуром (накриттям) необхідно об'єднати максимальну кількість суміжних клітин, що містять одиниці (нулі).

3) Необхідно, щоб кожна одиниця (нуль) накривалася хоча б один раз.

4) Та сама одиниця (нуль) може охоплюватися декілька разів різними контурами.

5) Верхній і нижній рядки діаграми вважаються суміжними - їх можна вважати такими, якщо умовно згорнути діаграму в горизонтальний циліндр.

6) Лівий і правий стовпці також вважаються суміжними - діаграму можна умовно згорнути у вертикальний циліндр.

7) Кутові клітини також вважаються суміжними - діаграму можна умовно згорнути в тор.

8) У клітини, що містять прочерки (на даних наборах ПФ невизначена), можна записувати додаткові одиниці (нулі), що сприяє одержанню більш простого кінцевого булевого виразу. При цьому варто пам'ятати, що хоча б один раз необхідно накрити лише основні одиниці (нулі). Додаткові одиниці (нулі) можуть збільшувати сумарну кількість одиниць (нулів), що входять у накриття, а отже, зменшувати кількість змінних у результуючих кон`юнкціях (диз'юнкціях).

9) Результатом мінімізації є булевий вираз в ДНФ або КНФ. Кількість кон`юнкцій у ДНФ (диз'юнкцій у КНФ) відповідає кількості контурів (накриттів).

10) У кожну кон`юнкцію (диз'юнкцію) увійдуть тільки ті змінні, значення яких у межах контуру не змінюється (змінна входить у накриття тільки в прямій або інверсній формі).

При мінімізації по одиницях у результуючі кон`юнкції змінні входять у прямій формі, якщо відповідні їм рядки і стовпці діаграми помічені рискою. Змінні, пов'язані з рядками і стовпцями не поміченими рискою, входять у кон`юнкції в інверсній формі.

При мінімізації по нулях у результуючі диз'юнкції змінні входять у прямій формі, якщо відповідні їм рядки і стовпці не помічені рискою, у протилежному випадку диз'юнкції містять змінні в інверсному вигляді.

Ціллю мінімізації є одержання мінімальної ДНФ або КНФ, що містить мінімум членів, які мають мінімальну кількість змінних. Для цього необхідно меншою кількістю контурів охопити хоча б один раз кожну одиницю (нуль). При цьому необхідно намагатися, щоб у кожне накриття входило як найбільше суміжних одиниць (нулів).

На рисунку 3.1 показані діаграми Вейча при числі логічних змінних n=2, 3, 4. Для n > 4 діаграми містяться у [18].

Якщо набори змінних початкової таблиці істинності упорядковані по зменшенню їхніх десяткових еквівалентів, то варто скористатися діаграмами Вейча приведеними у [5,6].