DM_1 / Деталі машин КЛ [Стадник В. А

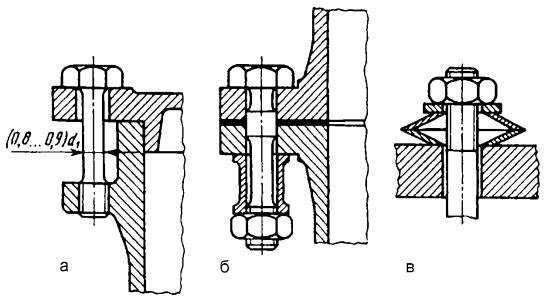
При визначенні податливостей системи болта, якщо болти короткі ( l < 6d ), враховують також податливість різьби і головки болта, для чого до розрахункової довжини болта l додають 1/2 висоти гайки.

Якщо коефіцієнт зовнішнього навантаження χ малий, то більша частина зовнішньої сили йде на розвантаження стику деталей, а менша – на додаткове навантаження болта. Тому з точки зору міцності стрижня болта необхідно

Рис. 19.31. Способи збільшення податливості елементів болтового з’єднання

збільшити податливість елементів корпусу. Для цього застосовують податливі болти (рис. 19.31, а, б), вводять в систему болта втулки (рис. 19.31, б), пружинні шайби і пружини (рис. 19.31, в), зменшують товщину деталей системи корпусу (особливо прокладок), а для зменшення контактних деформацій поліпшують якість обробки поверхонь стику. З цією ж метою застосовують матеріали з малим модулем (наприклад, титанові болти, що мають Eδ =1,1·104 МПа, в

стальних корпусах).

Визначення податливості деталей системи корпуса пов’язане з деякими трудностями. Площа поперечного перерізу деталей може бути дуже великою.

550

Для визначення коефіцієнта податливості λ∂ з’єднуваних деталей користуються методом, започаткованим проф. Н.І. Бобариковим. При дії осьової сили від гайки (головки болта) деформація концентрується поблизу стінок отвору, суттєво знижуючись по мірі віддалення від стінок.

За Н.І. Бобариковим, деформації з’єднуваних деталей розповсюджуються переважно на об’єм матеріалу в границях умовного конічного стрижня, який назвали „ конусом тиску ” ( рис. 19.32). Кут нахилу твірної конуса до осі на

Таке допущення дозволяє замінити деталь з невизначеною площею деталі

A∂ конічними втулками, податливість яких легко визначити. Для подальшого спрощення задачі конічну втулку можна замінити циліндричною з тим же об’ємом матеріалу і податливістю, що має зовнішній діаметр

551

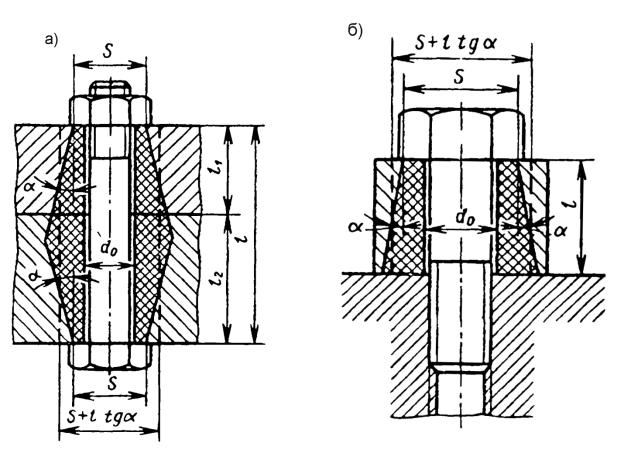
Рис. 19.32. „ Конуси тиску ” у з’єднанні.

Враховуючи вирази (19.57) і (19.58), можна записати, що зовнішні діаметри циліндричних втулок D визначиться за формулами:

Якщо на стику деталей є пружна (податлива прокладка, то податливість деталі значно зростає, а значить, зростає навантаження на болт (шпильку)).

Коефіцієнт податливості λ∂ визначають у такому випадку як суму коефіцієнтів податливості деталей і прокладки:

552

19.7. Поняття про розрахунок групового болтового з’єднання

Якщо болтове з’єднання здійснюється групою болтів, то розрахунок зводиться до визначення найбільш навантаженого болта і знаходження його діаметра викладеними вище методами. Решта, менш навантажених болтів з’єднання, приймаються (з метою уніфікації) того ж діаметра, що йде в запас міцності.

У розрахунках цих з’єднань припускають такі допущення:

а) деталі з’єднання достатньо жорсткі і поверхні стику деталей залишаються плоскими після навантаження з’єднання;

б) усі болти з’єднання мають однакові розміри і однакову затяжку; в) болти у з’єднанні розміщенні симетрично відносно двох

взаємноперпендикулярних осей, які проходять через центр ваги площини стику деталей. Перелічені допущення можна брати для більшості конструкцій, що зустрічаються на практиці.

В залежності від зовнішнього навантаження розрізняють чотири основні розрахункові випадки або їх комбінації:

1)група болтів навантажена силами, рівнодіюча яких перпендикулярна площині стику і проходить через його центр ваги. Подібний розрахунок розглянутий нами раніше (див. рис. 19.28);

2)група болтів навантажена поперечними силами, що діють в площині стику. Метод розрахунку подібних болтів була розглянута (див. рис. 19.25 і рис. 19.26), в допущенні рівномірного розподілу зусиль між усіма болтами групи;

3)група болтів навантажена моментом, що діє в площині стику (при

передачі крутного моменту). Сюди відносяться болти, що скріпляють півмуфти глухої дискової муфти (див. рис.18.4).

Розглянемо один із можливих варіантів закріплення гвинтами кронштейна (рис. 19.33, а) навантаженого асиметричною силою F .

553

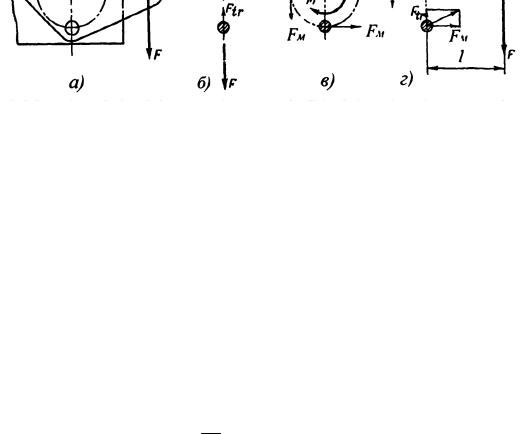
Припустимо, що кронштейн закріплений чотирма гвинтами, центри перерізів яких знаходяться на колі з радіусом r і розташовані симетрично поздовжньої осі симетрії кронштейна. Для спрощення розрахунків допустимо, що під дією сили F кронштейн повертається відносно центра кола. В дійсності центр ваги кронштейна зміщений по осі його симетрії в сторону лінії дії сили F . Таке спрощення розрахунку підвищує запас міцності гвинтів, так як збільшує розрахункове навантаження в порівнянні з дійсним (плече сили l більше дійсного плеча).

Дія симетричної сили F (рис. 19.33, а) може бути замінена симетричною

Рис. 19.33. Схема асиметричного навантаження гвинтів у кріпленні кронштейна з рівномірним розташуванням на колі центрів перерізу гвинтів

силою F (рис. 19.33, б) і моментом M (рис. 19.33, в). Виходячи із прийнятих допущень, вважаємо, що сила зсуває кронштейн по відношенню до станини. При цьому, на кожний із 4-х гвинтів діє сила

Ftr = F ,

z

де z - кількість гвинтів. Момент M = Fl повертає кронштейн відносно станини. При цьому сила, що діє на кожен із гвинтів, дорівнює коловій силі

(рис. 19.33, в)

554

Скориставшись принципом незалежності дії сил на гвинт, складаємо схему навантаження гвинтів, із якої витікає, що найбільш навантаженим буде гвинт, для якого діючі сили Ftr і Fм співпадають за напрямом дії.

Тоді згідно зі схемою (рис. 19.33. г)

а розрахункова сила для найбільш навантаженого гвинта з урахуванням його скручування при затяжці

де z - число болтів.

555

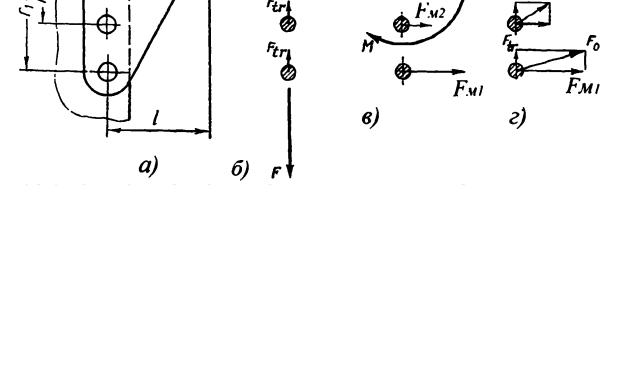
Рис. 19.34. Схема навантаження болтів кронштейна:

а– схема кронштейна;

б– схема навантаження болтів силою F ;

в– схема навантаження болтів моментом Fl

Максимальне зусилля Fм1 під дією моменту Fl (рис.19.34,в )

здійснюється на крайні, найбільш віддалені від центру повороту О (центру ваги стику) болти.

556

За розрахункове беруть найбільше з добутих значень навантаження. Для даного з’єднання (рис. 19.34, г) найбільш навантаженими є крайні болти, для яких

а розрахункова сила для найбільш навантаженого болта з урахуванням його скручування при затягуванні

Цю силу використовують при визначенні діаметра болтів із умови міцності на розтяг (див. формулу 19.28). Для всіх болтів з’єднання назначають однакову затяжку, незважаючи на те, що вони сприймають різне навантаження.

До четвертого випадку відноситься навантаження групи болтів

системою сил, що знаходяться в площині, що проходить через одну із її

557

осей симетрії перпендикулярно площині стику. Подібний випадок навантаження з’єднання зустрічається найбільш часто: кріплення різних агрегатів, корпусних деталей, кришок, кронштейнів і т. д. Болти розміщують рівномірно по поверхні або периметру стику і затягують кожний з однаковою силою.

В цьому випадку (рис. 19.30) дія довільно діючої сили

перпендикулярно стику і в площині стику по осі ХХ, а також до моменту

M = R2 l2 − R1l1 . На рис. 19.35 приведені сили R1 , R2 і момент M показані пунктиром. Вважаємо, що основа стойки, повертаючись під дією моменту M , залишається плоскою.

558

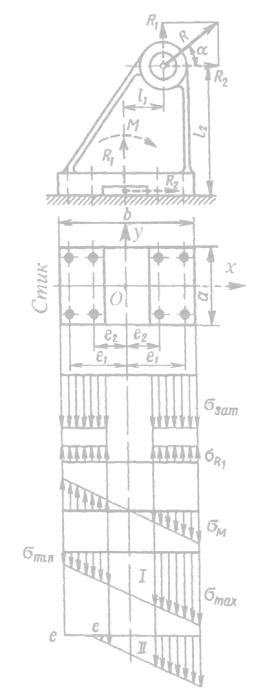
Рис. 19.35. З’єднання під дією сили відривання і моменту

Задача зводиться до визначення розрахункового навантаження на найбільш навантажений болт (а, отже, до визначення діаметра болтів) і сили затяжки, достатньої для надійного забезпечення щільності стику. Це вимагає на всіх ділянках стику напружень стиску. До прикладення сили R сила попередньої затяжки болтів Fзат створює у стику напруження зминання

559