
DM_1 / Деталі машин КЛ [Стадник В. А
.].pdf
[τ]зр - допустиме напруження на зріз.
З огляду на те, що для виготовлення болтів застосовують сталі звичайної якості, то допустиме напруження на зріз визначається в залежності від границі плинності [τ]зр == 0 ,3σП . Для сталі Ст3 σП =240 МПа.
Умова міцності за напруженнями зминання. Для середньої деталі:
σзм = |
|
F |
|
£ [σ]зм . |
(19.34) |
||
h2 |
× d0 |
|
|||||
|
|
× z |
|
||||
Для крайніх деталей |
|
|
|
|
|
||
σзм = |
|
|
F |
|
|
£ [σ ]зм. |
(19.35) |
|
|
|
|
||||
|
|
|
|
||||
|
2h1 × d0 × z |
|
|||||
Ці формули справедливі як для болта, так і для деталей, які з’єднуються цим болтом.
Допустимі напруження зминання визначаються для більш слабкого
матеріалу болта або деталі |
|
|
|
|
|
|
|
|
|||
|
|
|
[σ]зм = 0 ,4σП . |
|
|
|
(19.35) |
||||
Тоді діаметр болта дорівнює: |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
d0 ³ |
|
F |
|
або d0 |
³ |
|
F |
|
|
||
|
|
|
|
|
. |
(19.36) |
|||||
h2 |
× z[σ ]зм |
|
|||||||||
|
|
|
|
|
|
2h1 × z[σ ]зм |
|
||||
Розрахунок ведуть за гіршим варіантом, де товщина деталей меншаю Умова рівноміцності деталей:
2h1 = h2 .
За отриманими розрахунковими даними вибирають стандартний діаметр болта для гіршого варіанту (де діаметр болта більший).
Напружене болтове з’єднання (болт поставлений із зазором,
рис.19.26).
540
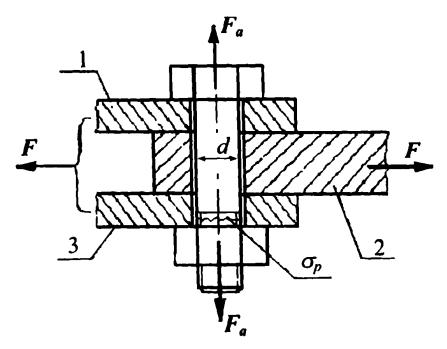
Умовою міцності з’єднання є відсутність відносного зсуву деталей. У цьому випадку зовнішнє навантаження F врівноважується силами тертя в стику, які створюються в результаті затягування болта. Розглядаючи рівновагу
Рис. 19.26. Схема для розрахунку болта, поставленого при поперечному навантаженні із зазором
деталі 2, одержимо умову відсутності зсуву деталей у стику. При спробі зсуву деталі 2 відносно 1 і 3, виникає сила тертя Fтр . Умова відсутності зсуву деталей має вигляд
Fтр ³ F або Fa f × i × z ³ KF , |
(19.37) |
де F - зовнішня сила, що діє на деталі з’єднання; K - запас зчеплення для запобігання зсувів у границях зазорів між болтами і отворами (при статичному навантаженні K =1,3…1,5, при змінному - K =1,8…2); f - коефіцієнт тертя,
рівний для сухих чавунних і сталевих поверхонь деталей машин f =0,15…0,2,
для необроблених поверхонь і металевих конструкцій f =0,3; z - число болтів.
Затяжку призначають з напруженням 0 ,6σ П , а в металевих конструкціях
до 0 ,8σП .
Згідно з формулою (19.26) умова міцності болта
541
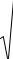
σ р |
= |
4FKβ |
£ [σ ]p , |
|
||||||
|
|
|
||||||||
|
|
|
fizπd1 |
2 |
|
|
|
|
||
Звідки внутрішній діаметр різьби болта |
|
|||||||||
|
|
|
|
|
|
|
|
|||
d |
|
³ |
|
4FKβ |
|
|||||
1 |
|
|
|
|
, |
(19.38) |
||||
|
|
|
||||||||
|
|
|
|
|
fizπ [σ ]p |
|
||||
де β - коефіцієнт, що враховує скручування болта при затяжці ( β =1,3); [σ ]p -
допустиме напруження на розтяг для болта
[σ ] = σ П p [S ] ,
де [S] - коефіцієнт запасу міцності, який залежить від діаметра болта і від того,
контролюється чи ні затяжка болта. Значення [S] при статичному навантаженні і неконтрольованій затяжці дані в табл. 19.1.
Таблиця 19.3. Допустимі коефіцієнти запасу міцності [S] при статичному навантаженні і неконтрольованій затяжці.
Матеріал болта |
|
|
Діаметр різьби |
||
6…16 |
|
16…30 |
|
30…60 |
|
|
|
|
|||
Вуглецева сталь |
5…4 |
|
4…2,5 |
|
2,5…1,5 |
Легована сталь |
6,5…5 |
|
5…3,3 |
|
3,3 |
При контрольованій затяжці |
коефіцієнт [S] |
не залежить від діаметра |
|||
болта. Для будь-якого болта із вуглецевої сталі при статичному навантаженні
[S]=1,3…2,5.
Порівнюючи навантажувальну здатність болтів, слід відмітити, що 10 болтів, поставлених з зазором при коефіцієнті тертя f =0,17, можна замінити одним болтом того ж діаметру, поставленим без зазору, значно дорожчі із-за складності технології виготовлення.
У випадку зсуву деталей болти зазнають деформації згину. Тому для розвантаження болтів від поперечної сили, а отже, зменшення діаметрів болтів, застосовують різні пристрої у вигляді шпонок, втулок (рис. 19.27, а), штифтів, зубців (рис. 19.27, б) і т.д.
542
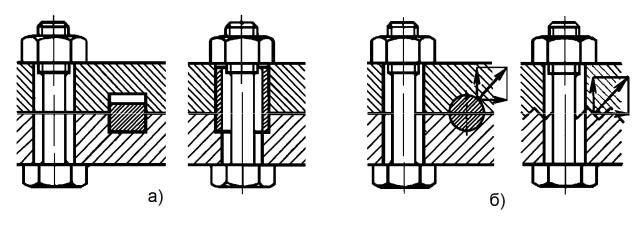
Рис. 19.27. З’єднання з болтами, розвантаженими від зсуву
У цьому випадку діаметри болтів приймають конструктивно, враховуючи можливість дії випадкових відривних сил і небезпеку розриву болтів при затяжці (рис. 19.27, а) або розраховують на розтяг віджимною силою, що виникає на поверхні контакту деталей (рис. 19.27, б).
Болти попередньо затягнуті, зовнішнє осьове навантаження розкриває стик. Болти з попередньою затяжкою застосовують для забезпечення герметичності з’єднання або недопустимості розкриття стику (кріплення кришок водяних помп, кришок циліндрів, корпусів і станин до фундаментів і т.д.).
Величина попередньої затяжки болта повинна бути такою, щоб після навантаження не виникло порушення герметичності або розкриття стику, тобто, щоб не появився зазор між з’єднуваними деталями.
Розглянемо затягнуте різьбове з’єднання, навантажене осьовим зовнішнім (робочим) навантаженням F (рис. 19.28, б). Визначимо повну силу, що розтягує болт (розрахункове навантаження), Fб. р. і необхідну для надійної
роботи з’єднання силу затяжки F0 .
543
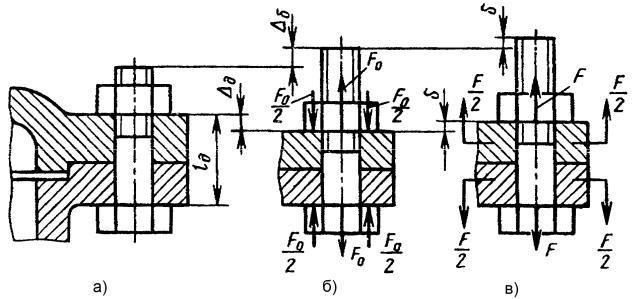
Рис. 19.28. Схеми деформацій деталей з’єднання після затяжки і при дії осьового зовнішнього навантаження
Задача про розподіл навантаження між болтом і стиком є статично невизначеною і розв’язується за допомогою сумісності переміщень. Очевидно, під дією зовнішнього навантаження в границях до розкриття стику болт подовжується на стільки, наскільки зменшується стискання деталей.
На рис. 19.28, а показане незатягнуте з’єднання. При затяжці гайка одержує осьове переміщення δ F , пропорційне куту повороту гайки (при повороті гайки на 360º δ F = p , де p - крок різьби). При цьому під дією сили
затяжки F0 стрижень болта розтягується на деяку величину δ , а з’єднувані деталі (фланці) стискаються (укорочується) на величину ∂ (рис. 19.28, б).
При цьому із умови рівноваги витікає, що сила, яка розтягує болт, дорівнює силі, що стискає фланці з’єднуваних деталей. Під дією зовнішньої сили F додатково відбувається розтяг болта на величину δ (див. рис. 19.28, в), при цьому початкове стискання ∂ зменшиться також на величину δ (див.
рис. 19.28, б і в).
Сили, що виникли в болті і стягуваних деталях, можна визначити із діаграми зусиль (рис. 19.29). Криві деформування (прямі при пружному навантаженні) болта і деталей показані на діаграмі у вигляді променів ОΙ і ОΙΙ. Вони описують залежності зусиль у болті і деталях від їх подовження при
544
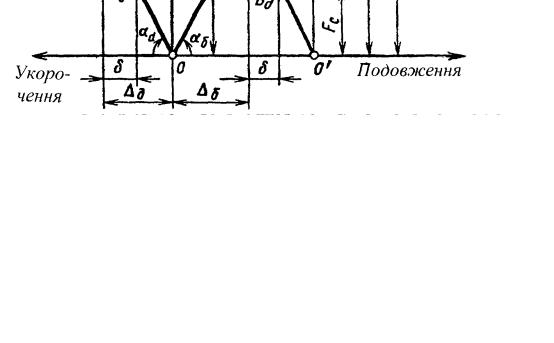
Рис. 19.29. Діаграма зусиль в затягнутому болтовому з’єднанні.
розтязі (укорочення при стиску). Точки Bδ і B∂ на діаграмі характеризують зусилля і деформації в болті і стягуваних деталях після затяжки.
Згідно з законом Гука
δ = F0 |
|
lδ |
|
|
= λδ F0 ; |
(19.39) |
E A |
||||||
|
δ |
δ |
|
|
||
¶ = -F0 |
|
l∂ |
|
|
= -λ∂ F0 , |
(19.40) |
E |
A |
|||||
|
|
∂ |
∂ |
|
|
|
де lδ і l∂ - довжина деформованої частини болта і стягування деталей; Eδ і
E∂ - модуль пружності матеріалу болта і деталей; Aδ і A∂ - площі поперечних перерізів болта і деталей; λδ і λ∂ - податливості болта і деталей (переміщення під дією сили в 1 Н);
λδ |
= |
lδ |
; |
λ∂ = |
l∂ |
|
. |
(19.41) |
Eδ × Aδ |
E∂ × |
|
||||||
|
|
|
|
A∂ |
|
|||
Неважко помітити, |
що кути нахилу прямих λδ |
і λ∂ характеризують |
||||||
відповідно жорсткості болта і деталей і визначаються за формулами:
545
tgαδ = |
|
|
F0 |
= |
|
|
|
F0 |
|
|
|
|
|
= |
1 |
|
; |
(19.42) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λδ |
|
|||||||||||||||
|
|
|
|
|
|
|
δ |
|
|
|
|
|
F0 × λδ |
|
|
|
|
|
||||||||||||||
tgα∂ |
= |
|
F0 |
|
= |
|
|
|
F0 |
|
|
|
|
= |
|
1 |
. |
(19.43) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
F0 × λ∂ |
|
λ∂ |
|
|
|
|||||||||||||
Із діаграми видно, що сила, яка розтягує болт, збільшиться на величину |
||||||||||||||||||||||||||||||||
F |
|
|
= δ × tgα |
δ |
= |
|
δ |
. |
|
|
|
(19.44) |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λδ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Сила, що стискає деталі, зменшиться на величину |
|
|||||||||||||||||||||||||||||||
F |
|
|
= δ × tgα |
∂ |
= |
δ |
|
. |
|
|
|
|
(19.45) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ∂ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Зусилля і деформація болтів і деталей будуть характеризуватися при |
||||||||||||||||||||||||||||||||
цьому точками B * і B |
|
* |
|
. Зниження сили в деталях можна знайти, сумістивши |
||||||||||||||||||||||||||||
δ |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
на діаграмі промені ОΙ і ОΙΙ (провівши через точку Bδ |
пряму О´ΙΙ´, паралельну |
|||||||||||||||||||||||||||||||
ОΙΙ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Із умови рівноваги витікає, що F = Fδ + F∂ . Підставивши у цю формулу |
||||||||||||||||||||||||||||||||
вирази (19.44 і 19.45) одержимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
= δ |
|
λδ |
+ λ∂ . |
|
|||||||||||||||||||
|
|
+ |
|
|
|
|
|
|
||||||||||||||||||||||||
|
λ |
|
|
|
|
|
λ |
|
|
|
|
|
||||||||||||||||||||
F = δ |
|
|
|
|
|
|
∂ |
|
|
|
λ × λ |
∂ |
|
|||||||||||||||||||
|
|
|
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
|||||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = F |
|
λδ × λ∂ |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
λ |
|
+ λ |
∂ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
|
|
|
|
|
|
|
|
|
||||||||
Але δ = Fδ × λδ . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Тоді F |
× λ |
|
|
|
= |
|
|
λδ × λ∂ |
, |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
δ |
|
|
|
δ |
|
|
λδ |
|
+ λ∂ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
звідки визначаємо додаткове зусилля на болт |
|
|||||||||||||||||||||||||||||||
Fδ |
= |
|
|
|
|
λ∂ |
|
|
|
|
F = χF , |
|
|
(19.46) |
||||||||||||||||||
|
|
λδ |
+ λ∂ |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
546 |
|
|
||||
де χ - коефіцієнт зовнішнього навантаження, що залежить від податливості болта та деталей з’єднання
χ = |
λ∂ |
|
|
|
λ + λ |
∂ |
|||
|
δ |
|
||
де χ - коефіцієнт зовнішнього |
навантаження; показує долю зовнішнього |
|||
(робочого) навантаження, що сприймається болтом у затягнутому з’єднанні (звичайно χ =0,2…0,4 для з’єднання металевих деталей):
χ = |
|
λ∂ |
. |
(19.47) |
|
λδ |
+ λ∂ |
||||
|
|
|
|||
Повна сила, що діє на болт (шпильку) |
|
||||
Fп = F0 + Fδ |
= F0 + χF . |
(19.48) |
|||
Задачі розрахунку різьбового з’єднання. Розрахунок різьбового з’єднання
включає в себе звичайно дві задачі: 1) оцінку міцності з’єднання; 2) оцінку щільності (герметичності) стику.
Міцність з’єднання визначається, як правило, міцністю болта (шпильки) і для її оцінки необхідно знати напруження в перерізі з найменшою площею.
Якщо зовнішнє навантаження на болт змінюється циклічно від 0 до F (див. рис. 19.29), то амплітуда змінних напружень у перерізі болта за внутрішнім діаметром різьби
|
|
σa = |
Fδ |
= |
|
χF |
|
|
(19.49) |
|
|
2 A1 |
2 A1 |
||||||||
|
|
|
|
|
|
|||||
і середнє напруження |
|
|
|
|
|
|
||||
σm |
= |
F0 + 0 ,5Fδ |
|
= |
F0 + 0 ,5 χF |
. |
(19.50) |
|||
A1 |
|
|||||||||
|
|
|
|
|
A1 |
|
||||
Щільність стику визначається залишковим зусиллям у стику. Зовнішнє |
||||||||||
навантаження F зменшує зусилля у стику деталей до величини |
|
|||||||||
Fc |
= F0 − F∂ = F0 − (1 − χ)F . |
(19.51) |
||||||||
547

Якщо зусилля у стику стане рівним нулю ( Fc =0), то стик розкриється
(розгерметизується) і все зовнішнє навантаження Fp буде сприйматись болтом,
що небезпечно для його міцності (особливо при змінному навантаженні). Для запобігання розкриття стику повинно бути
Fc > 0 ,
тоді мінімальна сила затяжки
Fmin > (1 - χ)F .
Звичайно призначають |
|
F0 =ν (1 − χ)F , |
(19.52) |
де ν - коефіцієнт запасу попередньої затяжки болта, який при статичному навантаженні з’єднання можна брати: за умови не розкриття стику деталей
з’єднання ν =1,2…2,0; за умови |
герметичності з’єднання |
ν =1,3…2,5 – при |
м’яких прокладках між деталями з’єднання; ν =2,0…3,5 – |
при металевій |
|
фасонній прокладці; ν =3,0…5,0 – |
при металевій плоскій прокладці. |
|
Розрахункова сила, що діє на болт, визначається із умови не розкриття стику на основі виразу (4.63) з урахуванням скручування болта при його затяжці (див. 4.52)
Fб. р. = F0 × β + χF . |
(19.53) |
Розрахункова сила на болт Fб. р., що визначається за формулою (19.53),
дозволяє розрахувати діаметр різьби болта за умовою міцності на розтяг:
d1 ³ |
4Fб. р. |
. |
(19.54) |
|
|||
|
π[σ ] |
|
|
Згідно зі значенням d1 назначають стандартний діаметр різьби.
Визначення коефіцієнта зовнішнього навантаження. Як видно із формули (19.47), для визначення коефіцієнта χ повинні бути відомі значення коефіцієнтів податливості болта (гвинта) λδ і деталей λ∂ .
548
У загальному випадку всі елементи з’єднання можна розділити на дві системи (див. рис. 19.18, а): систему болта, куди входять болт, шайби та інші елементи, сума абсолютних деформацій яких під дією зовнішнього навантаження зростає; систему корпуса, куди входять з’єднувані деталі, тобто фланці, кришки, прокладки та інші елементи, сума абсолютних деформацій яких під дією зовнішнього навантаження зменшується.
Коефіцієнт податливості болта визначається порівняно просто: для болта (гвинта) постійного перерізу
|
|
|
|
|
|
|
|
|
|
λб = |
lб |
|
, |
|
|
|
|
|
|
(19.55) |
|||
|
|
|
|
|
|
|
|
|
|
Eб × Aб |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де |
Aб = |
πdc |
2 |
4 ; dc - діаметр стрижня болта; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
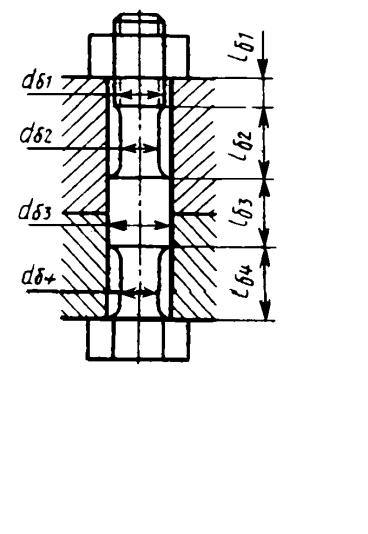
|
|
для болта змінного перерізу (рис. 19.30) |
|
|
|
|
|
||||||||||||||||
λ |
= |
1 |
|
n |
l |
бi |
= |
l |
б1 |
+ |
l |
б2 |
|
+ |
l |
б3 |
+ |
l |
б4 |
|
|
||
|
|
|
∑ |
|
|
|
|
|
|
. |
(19.56) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
δ |
|
|
Eб i =1 Aбi |
|
Eб Aб1 |
|
Eб2 Aб2 |
|
|
Eб Aб3 |
|
Eб A4 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
Рис. 19.30. Болт змінного перерізу
549
