DM_1 / Деталі машин КЛ [Стадник В. А

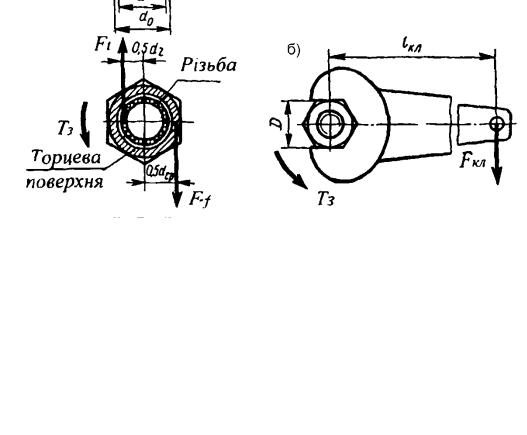
деталь, розтягуючи болт. При загвинчуванні гайки (рис. 19.12, а і б) осьова сила

F у стрижні болта зростає від 0 до необхідної сили затяжки Fзат ; при цьому збільшується і момент Ткл , що прикладається до гайки.

Рис. 19.12. Схема для визначення моменту тертя на торці гайки

Умову рівноваги моментів в загальному вигляді можна записати

Ткл = Т р + Тт , (19.2)

де Т р - момент в різьбі, що визначається за раніше одержаною формулою

(15.4)

Т р = F × tg(ψ + ϕ′)0 ,5d2 ,

де F - осьова сила затяжки; ψ - кут підйому гвинтової лінії; ϕ′ - зведений кут тертя в різьбі. Tт - момент тертя на торці гайки, що виникає при затяжці болта.

Визначення моменту тертя на торці гайки. Момент тертя на торці гайки або головки гвинта при їх загвинчуванні визначають наступним чином.

520

Торцева опорна поверхня гайки або головки гвинта (рис. 19,12. в) приймається кільцевою з зовнішнім діаметром D , рівним приблизно розміру під ключ S і

внутрішнім діаметром d0 , рівним діаметру отвору під болт, гвинт або шпильку.

Якщо прийняти, що при силі затяжки F питомий тиск q на опорній поверхні розподілений рівномірно, то можна записати

4F

q = π (D2 - d0 2 ).

Виділивши кільце товщиною dρ . Момент, що створюється силою тертя

dF × f на цій площадці дорівнює

dFт = dF × f = f × q × 2πρ × dρ × ρ .

Отже,

Для спрощення розрахунків часто приймають, що рівнодіюча сили тертя F × f на опорній поверхні гайки або головки гвинта діють по дотичній до кола середнього діаметра dcp (рис. 19.12,а), опорної поверхні і момент

521

Очевидно, що максимальний момент загвинчування (момент на ключі)

при заданій силі затяжки Fз визначається за формулою

в 1 Н, прикладена на кінці ключа, створює силу притискання деталі 60…100 Н. Такий виграш в силі забезпечує легкість складання з’єднання, але разом з тим він є небезпечним для малих діаметрів болтів. Не складно показати, що для зусилля робітника 300 Н, d =6 мм і нормальній довжині ключа lкл = 15d

напруження затяжки складе σ з =800 МПа, що перевищує границю плинності маловуглецевої сталі. Небезпека перетяжки болтів (шпильок) з діаметром d ≤10 мм обумовлює необхідність обмеження і контролю моменту затяжки. Цей момент на практиці вимірюють і задають за допомогою

динамометричних ключів.

Рис. 19.13. Динамометричний ключ:

1 – стрижень; 2 – рукоятка; 3 – пластина зі шкалою.

522

На рис. 19.13 показаний ключ, в якому момент затяжки пропорційний переміщенню стрілки на стрижні 1 з рукояткою 2 відносно пластини 3 (зі шкалою), жорстко зв’язаною з головкою ключа. В масовому виробництві застосовують пневматичні або електричні протаровані ключі.

Розподіл осьової сили, що діє на болт, на витках різьби

У з’єднанні болт-гайка осьове навантаження передається через різьбу

гайки. При цьому кожний виток різьби навантажується відповідно силами F1 ,

F2 ,… Fz . Сума всіх сил становить загальну осьову силу Fa на стрижні болта.

При розгляді сумісної роботи витків різьби болта і гайки (рис. 19.14)

насамперед виникає питання про розподіл осьового навантаження Fa на витках різьби. Якби було можливо знехтувати деформаціями розтягу болта і стиску гайки, тобто вважати їх абсолютно жорсткими у порівнянні з податливою

523

різьбою, то всі одночасно працюючі z витків одержали б однакові деформації і несли б однакове навантаження, мала б місце рівність

де z число витків різьби в гайці.

Теоретичне дослідження і експеримент показали, що нехтувати деформаціями болта і гайки не можна.

Задача про розподіл сил між витками болта і гайки є статично невизначеною.

Аналітичний розв’язок цієї задачі для нормальної гайки з десятьма витками ( z =10), виконаний вперше російським вченим М.Є. Жуковським (в 1902 році), показав, що навантаження розподіляється на витках різьби дуже нерівномірно (рис. 19.14). Найбільше навантаження сприймає перший найближчий до опорної поверхні виток ( F1 ≈ 0 ,34 Fa ), а останній, 10-й виток несе дуже мале навантаження ( F10 < 0 ,01Fa ).

Основною причиною нерівномірності є несприятливе поєднання деформацій болта і гайки. Під дією прикладеного до болта навантаження ділянка стрижня болта в зоні згвинчування подовжується на визначену величину, а відповідна їй ділянка гайки укорочується. Якщо дотикання до і після навантаження відбувається на всіх витках, то це означає, що деформація витків компенсує різницю деформацій стрижня болта і тіла гайки. Ділянки болта і гайки, розташовані ближче до опорної поверхні гайки, навантажені більшою силою, тому розтягуються і стискаються на більшу величину, а значить більше деформуються і витки різьби, що належать цим ділянкам, тобто ці витки передають більше навантаження. В міру передачі сили від болта до гайки у зв’язку з поступовим віддаленням від опорної поверхні гайки зменшуються навантажування ділянок болта і гайки і різниця їх деформацій. Витки різьби стають все менш навантаженими. Дослідження нерівномірності розподілу навантаження по довжині згвинчування для стандартної гайки з

524

шістьома витками при допущенні абсолютно точного виготовлення різьби показали, що перший від опорної поверхні виток сприймає 52% загального навантаження, а останній тільки 2%.

Силове поле у болті і гайці (рис. 9.15) досить явно показує нерівномірність розподілу сил між витками. Напрям силових ліній показує напрям головних напружень, густота силових ліній характеризує інтенсивність напружень.

Така різка нерівномірність розподілу навантажень на витках указує на те, що велике збільшення висоти гайки виявляється марним у зв’язку з небезпекою послідовного „ ланцюгового ” руйнування різьби.

Виходячи із цього положення, установлюється висота кріпильних гайок. Її вибирають рівною 5…10 крокам гвинтової лінії.

H = (5...10)p .

Норми на глибину загвинчування: в сталеву деталь H1 = d , в чавунну деталь H1 = 1,5d , в алюмінієву деталь H1 = (2 ,5...3)d , де p - крок різьби, d - зовнішній діаметр різьби.

На відміну від з’єднання болт-гайка у з’єднанні типу стяжки (рис. 19.16) тіла обох різьбових деталей випробовують на розтяг, тому розподіл навантаження між витками у цьому випадку близький до рівномірного.

Рис. 19.16. Розподіл навантаження у з’єднанні типу стяжки

525

У з’єднанні болт-гайка одним із ефективних шляхів вирівнювання навантаження на витках різьби є зміна конструкції гайки з метою заміни деформації стиску гайки деформацією розтягу. Для цього застосовують висячі гайки, гайки з торцевою проточкою і спеціальні конструкції розташування гнізд для шпильок в корпусних деталях (рис. 19.17, а, б, в).

Рис. 19.17. Конструктивні прийоми, що зменшують нерівномірність розподілу навантаження

між витками різьби Нерівномірність розподілу навантаження на витках різьби у з’єднанні

болт-гайка може бути також згладжена шляхом збільшення податливості витків різьби, наприклад, застосуванням гайок з утопленою різьбою (рис. 19.17, г), або зрізом частини нижніх витків (рис. 19.17, д), що робить нижні витки більш податливими.

526

Рис. 19.18. Розподіл навантаження на витках гайки:

а– стандартної;

б– з торцевою проточкою

На рис. 19.18, б показано вплив на розподіл навантаження у нижній частині гайки за рахунок торцевої проточки у порівнянні зі стандартною гайкою (рис. 19.18, б).

Крім деформування стрижня болта, тіла гайки і витків різьби на дійсний характер розподілу навантаження між витками впливають також місцеві пластичні деформації, неточність виготовлення і зношування різьби.

19.5. Розрахунок витків різьби на міцність

Врезультаті дії осьової сили у болтовому з’єднанні (рис. 19.19) по лінії ав

увитку гвинта і по лінії сє у витку гайки виникають напруження зрізу, а по лінії ас – зминання.

527

Рис. 19.19. До розрахунку витків різьби на міцність Враховуючи складність визначення навантаження на окремий виток

різьби, проводять умовний розрахунок різьби на зріз у припущенні рівномірного навантаження витків за допустимим напруженням, встановленим дослідним шляхом (на зминання, згин і зношування стандартні кріпильні різьби не розраховують):

а) для гвинта

нерівномірному розподілі навантаження між витками різьби. Для однорідних

528

матеріалів гвинта і гайки можна приймати K = 0 ,6 , для більш податливого

матеріалу гайки K m = 0 ,7 , для з’єднань шпильками K m = 0 ,8 , при використанні різьбових вставок K m = 1.

При однаковій міцності матеріалів гвинта і гайки розрахунку підлягає тільки різьба гвинта, так як d > d1 .

Умова зносостійкості ходової різьби за напруженнями зминання

де z = H p - число робочих витків (наприклад, число витків гайки).

Формула (19.18) є загальною для гвинта і гайки. З урахуванням припрацювання ходових різьб і при умові, що допустимі напруження приймають згідно накопиченому досвіду експлуатації, коефіцієнт Km

приймають рівним одиниці.

Висота гайки і глибина загвинчування. Однією із умов призначення висоти стандартних гайок є рівноміцність різьби і стрижня гвинта.

Прийнявши в якості граничних напружень границі плинності (рос.

текучести) матеріалу на розтяг і зсув і враховуючи, що τп ≈ 0 ,6σП , запишемо умови рівноміцності різьби на зріз і стрижня гвинта на розтяг у вигляді

Тут 4F πd12 - напруження розтягу в стрижні гвинта, розраховане приблизно

за внутрішнім діаметром різьби d1 .

529