
Конспект лекцій_лінійна алгебра / lek16_linalg
.pdf
Лекція 16
Квадратичні форми
16.1. Визначення квадратичної форми
Однорідний многочлен другого степеня від n змінних із дійсними коефіцієнтами називають квадратичною формою:
n |
|
|
|
|
a x2 |
2 |
a x x |
j |
, де a R . |
ii i |
|
ij i |
ij |
|
i 1 |
1 i |
j n |
|
|
Якщо в деякому просторі вибрати деякий базис, то про квадратичну форму можна думати, як про деяку функцію, значення якої визначається через
координати x1 ,...,xn вектора x .
Квадратичну форму можна записати в матричному вигляді:
xT Ax ,
де x x1 ,...,xn - стовпець, що складений із змінних; A aij -
симетрична матриця порядка n , що називається матрицею квадратичної
форми.
Ранг матриці А квадратичної форми називають рангом квадратичної форми. Якщо матриця А має найбільший ранг, що дорівнює кількості змінних n , то квадратичну форму називають невиродженою, а якщо rangA n, то її називають виродженою.
◄Приклад 16.1. Знайти матрицю квадратичної форми |
x2 |
4x x |
і |
|
|
1 |
1 |
2 |
|
визначити її ранг.
Розв’язання.
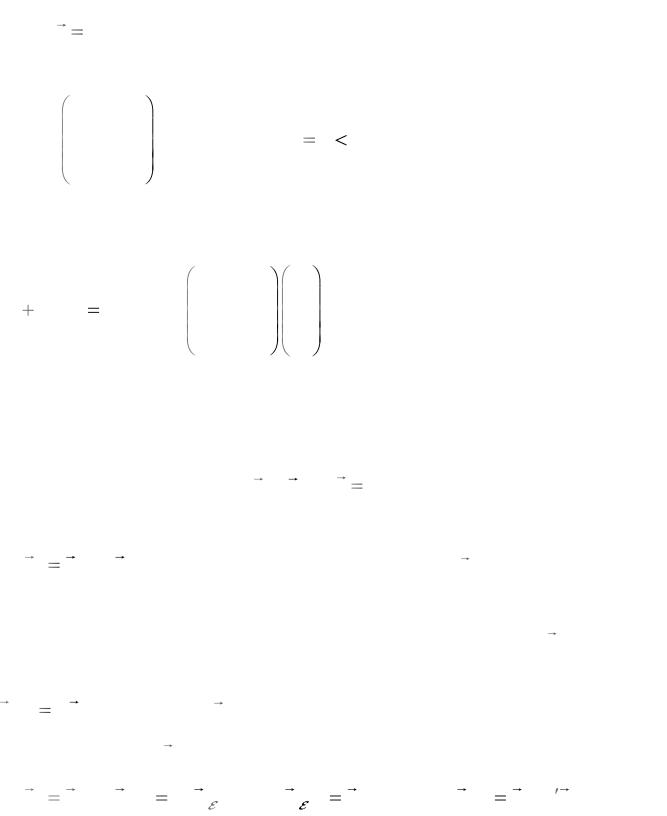
Матриця квадратичної форми складається для визначення функції від
вектра x x1 ,x2 ,x3 . Якщо доданки квадратичної форми відсутні, це
означає, що відповідні коефіцієнти дорівнюють нулю. Тоді матриця має
1 |
0 |
2 |
|
вигляд: 0 |
0 |
0 |
. Оскільки rangA 2 3, то ця квадратична форма є |
2 |
0 |
0 |
|
виродженою.
В матричному вигляді квадратична форма має вигляд:
|
|
|
|
|
1 |
0 |
2 |
x1 |
|
x2 |
4x x |
x x x 0 |
0 |
0 |
x |
.► |
|||
1 |
1 |
2 |
1 |
2 |
3 |
|
|
2 |
|
|
|
|
|
|
2 |
0 |
0 |
x3 |
|
16.2. Перетворення квадратичних форм
Нехай дана квадратична форма xT Ax , де x |
x ,x ,x |
T . В n -вимірному |
|||
|
|
1 |
2 |
3 |
|
лінійному просторі L з фіксованим базисом B вона визначає функцію |
|||||
f x |
xTB Ax B , що задана через координати вектора x в базисі B . |
||||
Знайдемо запис цієї ж функції в деякому іншому базисі E . Нехай U -
матриця переходу від базиса B до базиса E . Координати вектора x в
старому і в новому базисах будуть пов’язані співвідношенням:
x B Ux E . Функція |
f x |
в новому базисі буде виражатися через нові |
||||||
координати вектора x наступним чином: |
|
|
|
|
|
|
||
T |
|
T |
T |
|
T |
|
T |
|
f x x B Ax B |
|
|
|
AU x E |
A x E . |
|||
Ux |
A Ux |
x E |
U |
|
x E |
|||
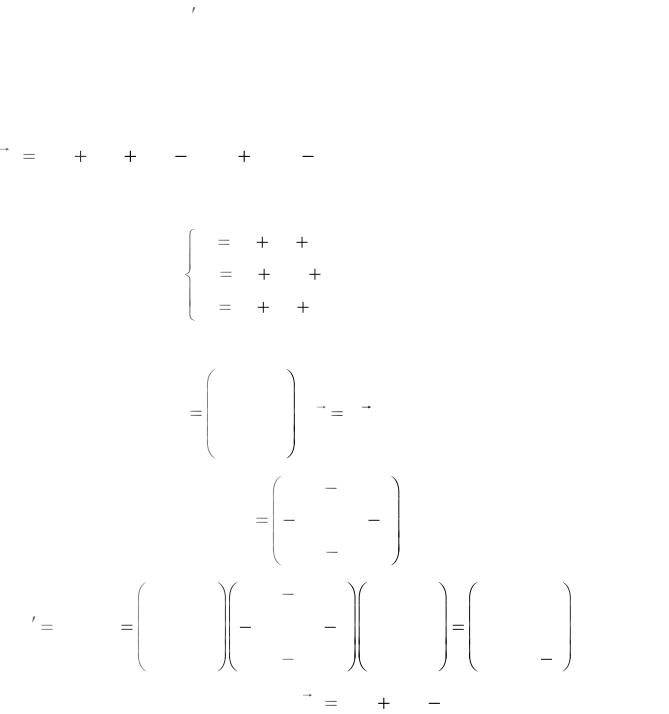
Отже, функція f в новому базисі також записується, як квадратична форма, причому матриця A цієї квадратичної форми зв’язана із матрицею А співвідношенням: A
◄Приклад 16.2. Квадратичну форму |
|
|
|
|
||||||
f x 7x2 |
5x2 |
2x2 |
8x x |
|
2x x |
6x x |
перетворити до нових |
|||
1 |
2 |
3 |
1 |
2 |
|
1 |
3 |
2 |
3 |
|
координат |
y1 , y2 , y3 |
, де старі і нові координати пов’язані системою: |
||||||||
|
|
|
x1 |
|
y1 |
y2 |
|
y3 |
|
|
|
|
|
x2 |
|
y1 |
2 y2 |
2 y3 . |
|
||
|
|
|
x3 |
|
y1 |
y2 |
2 y3 |
|
|
|
Розв’язання. Матриця переходу до нового базиса має вигляд:
1 |
1 |
1 |
|
U 1 |
2 |
2 |
і x Uy . |
1 |
1 |
2 |
|
|
|
|
|
7 |
4 |
1 |
|
|
|
|
|
|
Матриця А квадратичної форми: A |
4 |
5 |
3 . |
|
|
|
|
|
||||
|
|
|
|
1 |
3 |
2 |
|
|
|
|
|
|
1 |
1 |
1 |
7 |
4 |
1 |
1 |
1 |
1 |
|
2 |
0 |
0 |
Тоді, A U T AU 1 |
2 |
1 |
4 |
5 |
3 |
1 |
2 |
2 |
|
0 |
3 |
0 |
1 |
2 |
2 |
1 |
3 |
2 |
1 |
1 |
2 |
|
0 |
0 |
1 |
Квадратична форма набуває вигляду: f |
y |
2y2 |
3y2 |
|
y2 |
.► |
|
|
||||
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
16.3. Квадратичні форми канонічного вигляду

|
|
x2 ... |
x2 |
|
|
|
|
|
Квадратичну форму |
1 |
, |
i |
R, i 1,n , що не має попарних |
||||
|
1 |
n n |
|
|
|
|
||
добутків змінних, називають квадратичною формою канонічного
вигляду. Змінні, в яких квадратична форма набуває канонічного вигляду називають канонічними змінними.
Метод Лагранжа зведення квадратичної форми до канонічного вигляду.
Основу метода складає алгоритм послідовного виділення повних квадратів і введення нових відповідних змінних.
◄Приклад 16.3. Методом Лагранжа звести до канонічного вигляду
квадратичну форму x2 |
4x x . |
|
|
|
|
|
|
|||||
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
Розв’язання. Виділимо повний квадрат по x1 : |
|
|
|
|
||||||||
x2 |
4x x |
x2 |
4x x 4x2 |
4x2 |
x 2x |
2 |
4x2 . |
|||||
1 |
1 |
2 |
1 |
|
1 |
2 |
2 |
2 |
1 |
2 |
2 |
|
Введемо нові змінні: z1 |
x1 |
|
2x2 ; z2 |
2x2 . В цих змінних квадратична |
||||||||
форма набула канонічного вигляду: z2 |
z2 .► |
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
Канонічний вид, до якого приводиться квадратична форма, визначається неоднозначно: ввевши заміну z1 x1 2x2 ; z2 x2 ми отримали б вигляд
z12 4z22 .
Метод Якобі зведення квадратичної форми до канонічного вигляду

Метод Якобі можна застосовувати лише тоді, коли всі головні мінори матриці квадратичної форми відмінні від нуля. Нехай задано квадратичну
форму xT Ax , де xT |
x ,x |
,...,x |
. Якщо всі головні мінори матриці |
|
1 2 |
n |
|
квадратичної форми відмінні від нуля, то існує єдине невироджене однорідне перетворення змінних вигляду:
x1 y1 |
21 y2 |
... |
n1 yn |
|
x2 |
y2 |
32 y3 |
... |
n2 yn . |
... |
|
|
|
|
xn |
|
|
|
yn |
Це перетворення координат приводить квадратичну форму до канонічного
|
|
n |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
вигляду |
|
j y2j , де |
1 |
1 , |
j |
|
|
|
; |
j |
|
2,n. |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
j |
1 |
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
Коефіцієнти розкладання |
|
|
1 j |
i |
|
j |
1i |
, де |
|
|
мінор матриці |
|||||||||
ji |
|
|
|
|
|
|
j 1i |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
квадратичної форми, розташований на перетині перших |
j 1 |
рядків та |
||||||||||||||||||
перших j |
стовпчиків за винятком i |
ого стовпчика. |
|
|
||||||||||||||||
◄Приклад 16.4. Привести квадратичну форму |
|
|
|
|
||||||||||||||||
xT Ax |
x2 |
2x2 |
x2 |
6x x |
2x x |
|
до канонічного вигляду методом |
|||||||||||||
|
|
1 |
2 |
3 |
1 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|||
Якобі. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
0 |
|
1) |
Складемо матрицю квадратичної форми: A |
3 |
2 |
1 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
Обчислимо всі головні мінори: |
|
|
|
1, |
|
|
|
3 |
|
11, |
|
|||||||||
|
|
|
|
|
|
1 |
|
|
||||||||||||
1 |
|
|
|
2 |
|
3 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
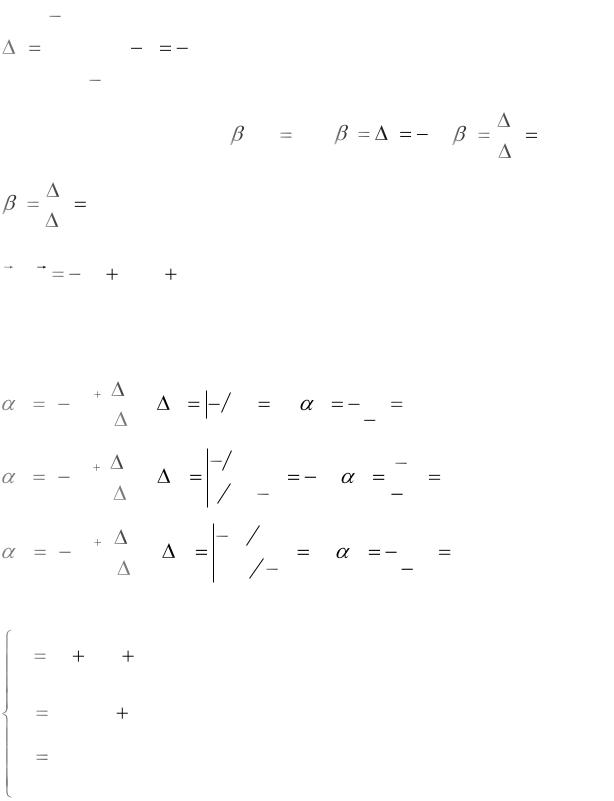
|
|
|
1 |
|
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
2 |
1 |
|
|
10 . Всі головні мінори не дорівнюють нулю. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1; 2 |
|
2 |
11; |
2) Знайдемо коефіцієнти |
j ; j 1,3: 1 |
|
|
||||||||||||||||||
1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
10 |
. Отже, канонічний вигляд квадратичної форми: |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
11 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
T |
By |
y |
2 |
11y |
2 |
10 |
y |
2 |
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
2 |
11 |
3 |
|
|
|
|
|
|
|
|
||||
3) Знайдемо невироджене перетворення, що приводить квадратичну форму до канонічного вигляду:
21
31
32
1
1
1
2 1 |
11 |
; |
|
||||
|
|
|
|||||
|
|
|
|
11 |
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 1 |
21 |
; |
|
||||
|
|
|
|||||
|
|
|
|
21 |
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
2 |
|
22 |
; |
|
||
|
|
|
|
||||
|
|
|
22 |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 3 |
|
3; |
21 |
|
|
3 |
|
3; |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|||||||||||
1 3 |
0 |
|
|
3; |
|
|
3 |
|
|
|
3 |
; |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|||||
3 |
2 |
1 |
|
|
|
|
|
11 |
|
11 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
1 3 |
0 |
|
1; |
|
|
|
|
1 |
|
|
|
|
1 |
. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|||||
3 |
2 |
1 |
|
|
|
|
|
11 |
11 |
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким чином, шукане перетворення має вигляд:
x |
y |
3y |
|
3 |
|
y |
|
||||
|
|
|
|
|
|
|
|||||
1 |
1 |
|
2 |
11 |
3 |
|
|||||
x |
|
y |
|
1 |
|
y |
|
.► |
|||
|
|
|
|
|
|
|
|||||
2 |
|
2 |
11 |
3 |
|
||||||
x3 |
|
|
|
|
|
|
|
y3 |
|
||
16.4. Ортогональні перетворення квадратичних форм

Будемо розглядати евклідів простір і базиси вибирати ортонормовані. В
цьому випадку матриця переходу U буде ортогональною, а відповідне перетворення буде називатися ортогональним.
Теорема 16.1. При ортогональному перетворенні квадратичної форми характеристичне рівняння його матриці не змінюється.
Доведення. Нехай А – матриця заданої квадратичної форми. При ортогональному перетворенні ця матриця змінюється за формулою
A U T AU , де U -ортогональна матриця, яка має обернену U 1 U T .
Тоді A U 1 AU . Отже, матриці A і A - подібні і їх характеристичні рівняння співпадають. ●
Теорема 16.2. Будь-яку квадратичну форму ортогональним перетворенням можна звести до канонічного вигляду.●
З теореми випливають наступні важливі зауваження:
1)Діагональними елементами матриці A квадратичної форми канонічного вигляду, що отримана ортогональним перетворенням, є власні числа матриці А квадратичної форми. Це означає, що ми можемо записувати матрицю A канонічного вигляду, не шукаючи відповідне перетворення.
2)При відшуканні ортогонального перетворення, що зводить квадратичну форму до канонічного вигляду, ми відшукуємо базис з власних векторів відповідного самоспряженого оператора.
◄Приклад 16.5. Квадратичну форму x2 |
4x x |
ортогональним |
|
1 |
1 |
2 |
|
перетворенням привести до канонічного вигляду.
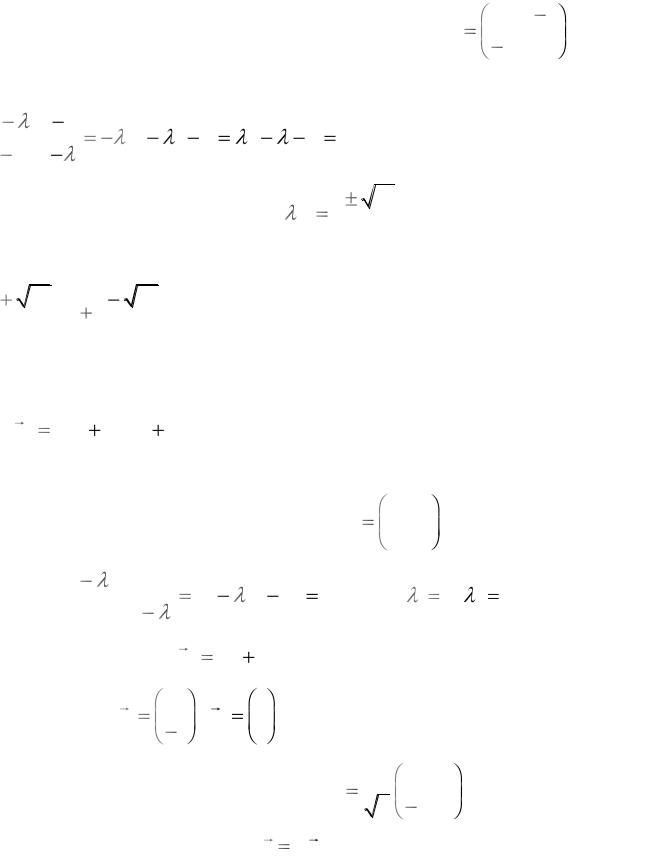
Розв’язання. Матриця квадратичної форми має вигляд: A |
1 |
2 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
Знайдемо характеристичне рівняння цієї матриці: |
|
|
||||||||||||
|
|
2 |
|
1 |
4 |
2 |
4 0 . |
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Корені характеристичного рівняння: |
|
|
1 17 |
. |
|
|
||||||||
1,2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отже, канонічний вигляд нашої квадратичної форми:
1 |
17 |
y2 |
1 |
17 |
y2 . ► |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
◄Приклад 16.6. Знайти канонічний вигляд квадратичної форми |
||||||||||||||||||
|
f |
x 5x2 |
|
8x x |
5x2 |
, до якого вона приводиться ортогональним |
||||||||||||
|
|
|
|
1 |
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
||
перетворенням в вказати одне з ортогональних перетворень. |
||||||||||||||||||
Розв’язання. Матриця квадратичної форми A |
5 |
4 |
, характеристичне |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
|
||
рівняння |
|
|
|
4 |
|
|
|
5 |
2 |
16 0. Корені |
1 |
1; 2 9 . |
||||||
5 |
|
|
|
|
|
|||||||||||||
|
|
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
||
Канонічний вигляд: f |
|
y |
y2 |
9y2 . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Власні вектори: e1 |
|
|
1 |
; e2 |
1 |
. Нормуємо вектори і складаємо |
||||||||||||
|
|
1 |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
матрицю ортонормованого перетворення: P |
1 |
|
1 |
1 |
||||||||||||||
|
|
1 |
1 . Цій матриці |
|||||||||||||||
|
|
|
||||||||||||||||
2 |
|
|||||||||||||||||
відповідає лінійна заміна змінних x |
Py .► |
|
|
|
|
|
||||||||||||

Теорема 16.3. Нехай A : E |
E - самоспряжений оператор. Функція |
|
f x |
Ax,x , що визначена в евклідовому просторі, є квадратичною |
|
формою. І навпаки, для будь-якої квадратичної форми f x в
евклідовому просторі існує такий самоспряжений оператор А, що
f x Ax,x і цей оператор визначений однозначно.
Доведення. 1) Використаємо запис скалярного добутку в ортонормованому базисі і врахуємо самоспряженість:
Ax,x x, Ax xT Ax ,
x - вектор стовпець, А – матриця лінійного оператора А. Отримали координатну форму запису квадратичної форми.
2)Нехай f x - квадратична форма, яка в заданому ортонормованому
базисі має вигляд xT Ax . Візьмемо самоспряжений оператор А, який має матрицю А в ортонормованому базисі. Тоді
f |
x |
xT Ax |
x Ax |
x, Ax |
Ax,x . |
|
3) |
Доведемо, що цей оператор – єдиний. Візьмемо два самоспряжених |
|||||
оператора А і В з матрицями А і В. Тоді, якщо виконується рівність |
||||||
Ax,x |
Bx,x |
для будь-якого x |
E , то A |
B . Дійсно, якщо |
||
записати відповідні квадратичні форми, то xT Ax |
xT Bx , тобто тут |
|||||
записана рівність двох многочленів другого степеня від n змінних. Така рівність можлива лише за умови рівності всіх коефіцієнтів при відповідних доданках, а це означає рівність матриць, а отже, і рівність операторів.●
16.5. Закон інерції

Квадратична форма може бути зведена до різних канонічних виглядів. Але існують характеристики коефіцієнтів квадратичних форм, що лишаються незмінними. Наприклад, якщо квадратична форма перетворилася до
вигляду |
1 |
y2 ... |
y2 |
, у якої всі коефіцієнти |
i |
невід’ємні, то |
|
1 |
n n |
|
|
відповідна квадратична функція приймає лише додатні значення, а з цього випливає, що жодний інший вид функції не буде містити від’ємних коефіцієнтів.
Теорема 16.4. Ранг квадратичної форми не змінюється при невироджених лінійних перетвореннях змінних і дорівнює:
А) кількості відмінних від нуля коефіцієнтів в будь-якому її канонічному вигляді;
Б) кількості ненульових власних значень матриці квадратичної форми з урахуванням їх кратності.●
В різних канонічних виглядах даної квадратичної форми залишається також незмінною кількість додатних та від’ємних коефіцієнтів.
Закон інерції. Теорема 16.5. Для будь-яких двох канонічних виглядів
f |
y |
y2 ... |
m |
y2 |
|
, |
i |
||
|
1 |
|
1 |
1 |
m |
|
|||
f |
2 |
z |
1 |
z2 ... |
k |
z2 |
, |
j |
|
|
|
1 |
k |
|
|
||||
однієї і тієї ж квадратичої форми:
0, i 1,m
0, j 1,k
-m k і їх спільна кількість дорівнює рангу квадратичної форми;
- |
кількість додатних коефіцієнтів |
i |
дорівнює кількості додатних |
|
|
|
коефіцієнтів j ;
