
Конспект лекцій_лінійна алгебра / lek12_linalg
.pdf
|
|
|
|
|
|
|
|
|
Лекція 12 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Лінійні простори |
|
|
|
|
|
||
|
|
|
|
|
|
12.1 . Поняття лінійного простору |
|
|
|
|||||||
Множину V називають лінійним або векторним простором, якщо: |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
є правило, за яким кожним двом елементам v1 |
,v2 |
V ставиться у |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відповідність |
третій елемент із V, який називають сумой v1 |
і v2 і |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
позначають |
v1 |
v2 : |
v1 |
,v2 |
V |
v1 |
v2 V ; |
|
|
|
|
|||||
2) |
|
є правило, за яким кожному елементу v |
V і будь-якому числу |
R |
||||||||||||
ставиться у відповідність елемент із V, який називають добутком елемента v |
||||||||||||||||
на число |
|
і позначають |
|
|
|
V , |
R |
|
|
V . |
|
|||||
|
|
v : |
v |
|
v |
|
||||||||||
Аксіоми лінійного простору: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v ,v1 ,v2 |
,v3 |
V , |
, |
|
R |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
v1 |
v2 |
v2 |
v1 ; |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
v1 |
v2 |
|
v3 |
v1 |
v2 |
v3 ; |
|
|
|
|
|
|
|
||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 V : v |
0 |
0 |
v |
v ; |
|
|
|
|
|
|
|
|||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( v ) : v ( v ) 0; |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
|
v1 |
v2 |
|
v1 |
|
v2 |
; |
|
|
|
|
|
|
||
6) |
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
v |
|
v ; |
|
|
|
|
|
|
|
|||
7) |
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
v ; |
|
|
|
|
|
|
|
|||||
8)1 v v .
Елементи лінійного простору називають векторами незалежно від їх
|
|
природи, вектор 0 називають нуль-вектором, а вектор ( |
v )― |
протилежним до вектора v .

Властивості лінійних просторів |
|
|
|
|
|||||
Наслідки з аксіом 1) – 8) |
|
|
|
|
|
||||
1) |
Існує тільки один нульовий вектор. |
|
|
|
|||||
2) |
Існує тільки один протилежний вектор. |
|
|
|
|||||
3) |
|
V |
|
|
|
|
|
|
|
u ,v |
рівняння u |
x |
v має єдиний розв’язок |
x |
v |
( u ) . |
|||
4) |
|
V : 0 |
|
0. |
|
|
|
|
|
v |
v |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
5) |
|
R : |
0 |
0. |
|
|
|
|
|
Приклади лінійних просторів
Для того, щоб з’ясувати чи є деяка множина лінійним простором відносно запроваджених на ній операцій і , необхідно перевірити виконання аксіом.
Лінійними є:
1)множина що містить лише нуль-вектор;
2)множина дійсних чисел;
3)множина n-вимірних векторів;
4)множина всіх геометричних векторів в просторі з початком в заданій точці і паралельних заданій площині;
5)множина всіх матриць m n , елементами яких є дійсні числа.
12.2. Базис лінійного простору
Базисом n― вимірного простору V називають будь-яку лінійно незалежну
|
цього простору і позначають B |
|
систему векторів vi n |
vi n . |

Базисом скінченної системи векторів називають не порожню лінійно незалежну її підсистему, через вектори якої виражається кожен вектор цієї системи.
Теорема 12.6. Якщо в n―вимірному просторі V задан базис B |
vi n , то |
|||||||
|
|
|
|
|
|
|
|
|
будь-який вектор x лінійно виражається через базисні вектори єдиним |
||||||||
чином. |
|
|
|
|
|
|
|
|
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Система векторів |
vi |
n ―лінійно незалежна, а система vi |
n ,x ―лінійно |
|||||
|
|
|
|
|
n |
|
|
|
залежна, отже |
i ,i |
1,n : x |
k vk (властивість 5 лінійної залеж- |
|||||
|
|
|
|
|
k |
1 |
|
|
ності).Доведено.● |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числа |
i називають координатами вектора x в базисі B , а вираз |
|
||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
k vk називають розкладанням вектора x по базисних векторах. |
|||||||
k |
1 |
|
|
|
|
|
|
|
Операції над векторами у вибраному базисі можна замінити операціями над їх координатами.
◄Приклад 12.4. Показати, що в R3 система векторів
a1 1, 1,2 , a2 2,1,0 , a3 |
4, 1,1 |
утворює базис і знайти в цьому |
|
базисі координати вектора |
c |
2,1,3 . |
|
Розв’язання. |
|
|
|
Покажемо, що вектори a1 |
1, |
1,2 , a2 |
2,1,0 , a3 4, 1,1 є лінійно |
незалежними. Складемо матрицю з координат векторів і знайдемо її ранг:
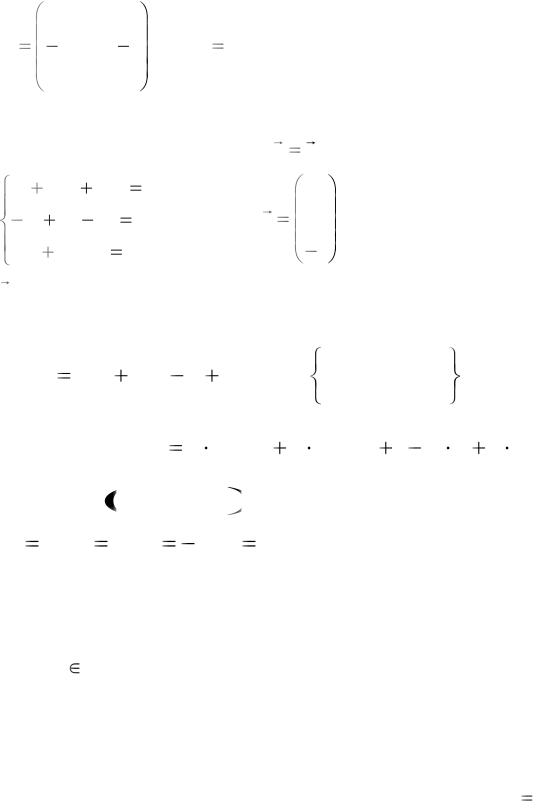
|
1 |
2 |
4 |
A |
1 |
1 |
1 ; det A 9 - матриця невироджена. Стовпці є лінійно |
|
2 |
0 |
1 |
незалежними, що означає лінійну незалежність системи векторів. Тоді,
розв’язавши матричне рівняння Ax |
c , або систему |
||||
x1 |
2x2 |
4x3 |
2 |
2 |
|
x1 |
x2 |
x3 |
1 , знаходимо x |
2 |
. Це і будуть координати вектора |
2x1 |
x3 |
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
c в новому базисі.► |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
◄Приклад 12.5. Знайти координати многочлена |
|
|
|
|||||||||||||||||
f ( x ) 4x |
3 |
3x |
2 |
x 3 |
в базисі |
2x |
3 |
, |
1 |
x |
2 |
, x,1 . |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Розв’язання. |
f ( x ) 2 ( 2x |
3 |
) 9 ( |
1 |
x |
2 |
) ( 1) x 3 1 |
. |
||||||||||||
|
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Координати |
|
f1 , f2 , f3 , f4 |
многочлена f ( x ) дорівнюють |
|
||||||||||||||||
f1 |
2, f2 |
|
9, f3 |
|
1, f4 |
|
|
3.► |
|
|
|
|
|
|
|
|
|
|
|
|
12.3. Розмірність лінійного простору
Нехай n N . Лінійний простір V називають n― вимірним, якщо вико-
нуються наступні аксіоми:
9)існують системи з n лінійно незалежних векторів;
10)будь-яка система з (n+1) вектора є лінійно залежною.
Число n називають розмірністю простору V і позначають dimV n .
Ранг будь-якої системи векторів в n― вимірному просторі не перевищує n.
◄Приклад 12.6. Задано однорідну систему лінійних рівнянь:
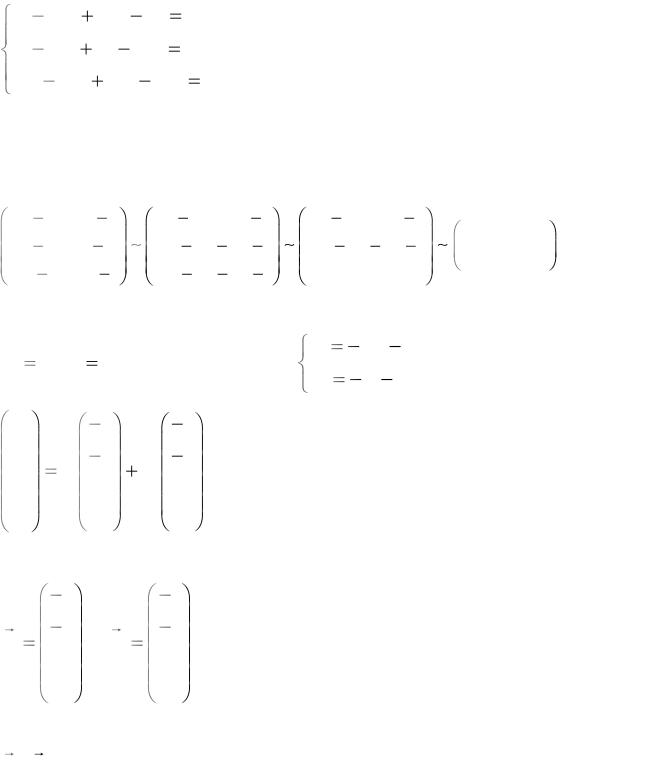
x1 2x2 2x3 x4 0
x1 3x2 x3 4x4 0 , множина розв’язків якої утворює лінійний
2x1 5x2 3x3 5x4 0
простір. Знайти розмірність цього простору і будь-який базис в ньому.
Розв’язання.
Розв’яжемо систему методом Гауса – Жордано:
1 |
2 |
2 |
|
1 |
|
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
0 |
4 |
5 . |
1 |
3 |
1 |
|
4 |
|
0 |
1 |
1 |
3 |
0 |
1 |
1 |
3 |
||||
2 |
5 |
3 |
|
5 |
|
0 |
1 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
3 |
|
|
|
|
|
|
||||||||||||
Ранг системи дорівнює 2, вільними змінними можемо вважати |
|
|
|||||||||||||||
x |
c ,x |
|
c |
, а базисними будуть |
x1 |
|
4c1 |
5c2 . |
|
|
|
|
|||||
3 |
1 |
4 |
|
2 |
|
|
|
|
|
x2 |
|
c1 |
3c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x1 |
|
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
c1 |
|
1 |
|
c2 |
3 |
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
0 . |
Це фундаментальна система розв’язків системи. |
|||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Згідно теорії систем лінійних алгебраїчних рівнянь система векторів |
|||||||||||||||||
|
|
4 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
f1 |
1 |
1 |
і |
f2 |
0 |
3 є лінійно незалежною, а будь-який інший розв’язок |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
може бути представлений у вигляді лінійної комбінації цих векторів. Вектори f1 , f2 утворюють базис в лінійному просторі розв’язків системи, що розглядається. Розмірність цього лінійного простору дорівнює 2 – кількості векторів в базисі.►

◄Приклад 12.7. Всі вектори з Rn , у яких перша та остання координати співпадають , утворюють лінійний підпростір в Rn . Знайти його базис і розмірність.
Розв’язання. Нехай множина M x ( x1 , x2 ,...,xn ) : x1 xn ―
заданий підпростір. Розглянемо систему векторів
e1 10...01 ; e2 |
010...00 ; e3 0010 00 ; ;en 1 00 010 .... ... ... |
||
|
|
|
|
Зауважимо, що ei |
M , i 1,n . Крім того, це повна система векторів в М: |
||
|
n |
дійсно |
iei 0 тільки при 1 |
i 1
xM : x ( x1 , x2 ,...,xn 1 ,x1 )
|
|
Отже, система векторів ei |
M , i |
dim M n 1.► |
|
... |
n |
0 |
. Тоді |
|
|
|
|
|
|
|
|
x1e1 |
|
x2e2 |
... xn 1en 1. |
1,n може бути базисом в М, .
12.4.Перетворення координат вектора при заміні базиса
Влінійному просторі всі базиси рівноправні. Іноді зручно використовувати для представлення елементів лінійного простору декілька базисів. В цьому випадку виникає задача перетворення координат векторів, що пов’язане із зміною базиса.
Нехай в n-вимірному просторі L задано два базиси: старий B |
bi in |
1 і |
||||||
новий C |
ci in |
1 . Будь-який вектор можна розкласти за базисом B . Тобто, |
||||||
кожен вектор з базису C можна представити у вигляді лінійної комбінації |
||||||||
векторів базису B : |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ci |
1ib1 ... |
nibi , i 1,n. |
|
|
||

1i
Або в матричному вигляді: ci B ... , або, для всіх векторів: C BU , де
ni
11 ... 1n
U ............ . Матрицю U називають матрицею переходу від старого
n1 ... nn
базису B до нового базису C . Згідно даному визначенню, i-ий стовпчик матриці переходу є стовпчик координат i-ого вектора нового базису в старому. Тому кажуть, що матриця переходу складається з координат векторів нового базису в старому, що записані стовпчиками.
Властивості матриці переходу.
1.Матриця переходу невироджена і завжди має обернену матрицю.
2.Якщо в n-вимірному просторі L задано базис B , то для будь-якої
невиродженої квадратної матриці U існує такий базис C в цьому ліній-
ному просторі, що U буде матрицею переходу від базису B до базису C .
◄Приклад 12.8. Нехай B = b1 ,b2 ,b3 - базис лінійного простору. Тоді
система векторів c1 |
2b1 , c2 |
b2 , c3 |
b3 також є базисом в цьому |
|||
|
|
|
2 |
0 |
0 |
|
лінійному просторі: |
c1 ,c2 ,c3 |
b1 ,b2 ,b3 |
0 |
1 |
0 |
.► |
|
|
|
0 |
0 |
1 |
|
3.Якщо U – матриця переходу від старого базиса до нового, то U 1 -
матриця переходу від нового базису до старого.
4.Якщо в лінійному просторі задано базиси B,C, D , причому U –
матриця переходу від базиса B до базису C , а V – матриця переходу від базиса C до базиса D , то добуток цих матриць UV – матриця переходу від базиса B до базиса D .
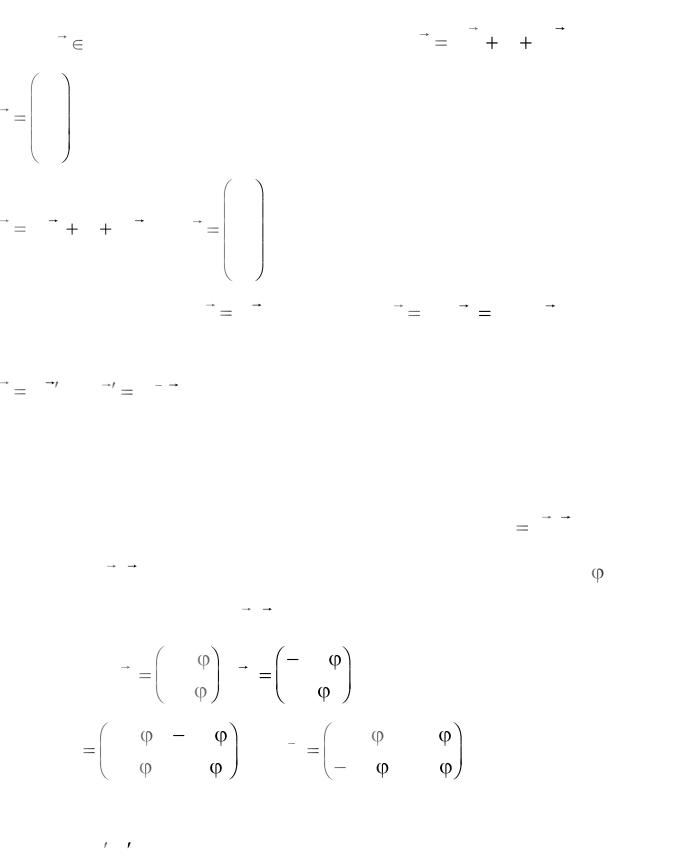
Дослідимо, як перетворюються координати довільного вектора в ліній-ному просторі при переході від старого базиса до нового. Виберемо довільний
вектор x L . Його розкладання за старим базисом: x x1b1 ... xnbn або
x1
x... . Розклад того самого вектора в новому базисі матиме вигляд:
xn
|
|
|
x' |
|
|
|
|
1 |
|
' |
' |
|
|
|
x x1 c1 |
... xncn |
або x |
... . Знайдемо зв’язок між старими та новими |
|
|
|
|
x' |
|
|
|
|
n |
|
координатами вектора: Bx |
Cx' . C = BU і Bx BUx' |
B Ux' . |
||
Згідно теореми про єдиність розкладання вектора за даним базисом, маємо:
x Ux або x U 1x . Отже, щоб отримати координати вектора в старому
базисі, необхідно стовбець координат цього вектора в новому базисі помножити зліва на матрицю переходу від старого базиса до нового.
◄Приклад 12.9. На площині задано ортонормований базис B |
i , j . |
||||||||
Новий базис e1 ,e2 |
отриманий поворотом старого базиса на заданий кут . |
||||||||
Знайти координати векторів |
e1 ,e2 |
нового базиса відносно старого. |
|||||||
Розв’язання. e1 |
cos |
; e2 |
sin |
. Матриця переходу матиме |
|||||
sin |
cos |
||||||||
|
|
|
|
|
|
|
|||
вигляд: U |
cos |
sin |
і U |
1 |
cos |
sin |
. |
|
|
sin |
cos |
sin |
cos |
|
|||||
|
|
|
|
|
|||||
Знайдені матриці дозволяють записати співвідношення між старими |
x1 ,x2 |
||||||||
та новими x1 ,x2 |
координатами довільного вектора площини: |
|
|||||||

x1 |
x1 cos |
x2 sin |
, |
x1 |
x1 cos |
x2 sin |
.► |
|
x2 |
x1 sin |
x2 cos |
, |
x2 |
x1 sin |
x2 cos |
||
|
12.4. Лінійний підпростір
Підпростором лінійного простору V називають множину U |
V , |
|||||||||
яка задовольняє умови: |
|
|
|
|
|
|
||||
1) |
якщо x, y |
|
U , то і x |
y |
U ; |
|
|
|
||
2) |
якщо x U , то і |
|
x |
U . |
|
|
|
|||
|
|
|
|
|
|
|
||||
Нехай vi V ,i |
1,m . Вектор виду |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
u |
1v1 |
|
2v2 ... |
mvm |
k vk |
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
називається лінійною комбінацією векторів vi |
з коефіцієнтами |
i . |
||||||||
Властивості підпросторів: |
|
|
|
|
|
|||||
1)якщо vi ,i 1,m ―елементи підпростору U , то і будь-яка лінійна
комбінація цих векторів буде елементом підпростору U ;
2)підпростір U є лінійним простором.
◄Приклад 12.1. Довести, що в лінійному просторі V 3 вільних векторів тривимірного простору лінійні підпростори утворюють: а) всі вектори, що паралельні заданій площині; б) всі вектори, що паралельні заданій прямій.
Розв’язання.
а) Перше твердження випливає з означення суми вільних векторів: вектори a
, b і a b - компланарні. Тому, якщо a , b паралельні деякій площині, то і a b буде паралельний цій площині. Якщо деякий вектор a помножити на число 0, то отримаємо вектор, що компланарний заданому і знову отримаємо вектор, що буде паралельний заданій площині.
Аналогічні міркування стосуються і випадку б).►

◄Приклад 12.2. В лінійному просторі C 0,1 всіх функцій, що неперервні на відрізку 0,1 знайти і описати можливі лінійні підпростори.
Розв’язання. Можна виділити наступні лінійні підпростори: а) множину функцій, неперервних на 0,1 і неперервно диференційованих в інтервалі
0,1 ; б) множину всіх многочленів. Зауважимо, що множина всіх монотонних функцій, що неперервні на 0,1 є підмножиною множини
C 0,1 але неє лінійним підпростором, оскільки сума двох монотонних функцій може не бути монотонною.►
12.5. Розмірність лінійного підпростору
Лінійний підпростір має розмірність та базис.
Теорема 2.4. Якщо H - лінійний підпростір лінійного простору
dim H dim L . Якщо до того ж H L , то dim H |
dim L . |
Доведення. Будь-який базис лінійного підпростору H є лінійно |
|
незалежною системою векторів у лінійному просторі |
L . Якщо цей базис в |
H є базисом і в L , то dim H dim L і зрозуміло, що в цьому випадку
H L. Якщо базис в H не є базисом в L , то існує такий вектор x L ,
який не є лінійною комбінацією векторів цього базиса. В цьому випадку лінійний підпростір не може співпадати із простором L . Додамо вектор x до векторів базису в H . Це означає, що в L знайдено більше лінійно
незалежних векторів, ніж . З цього випливає, що
З теореми випливає, що будь-який базис лінійного підпростору H
лінійному просторі L можна розширити, додавши вектор так, що розширена система векторів залишається лінійно незалежною. Отже, будь-який базис
