Метод Гаусса-Жордана (единичная матрица) (метод полного исключения)

Схема Гаусса-Жордана или метод полного исключения, заключается в одновременном исключении (Жордановом исключении) какого либо переменного из всех уравнений системы, кроме одного. Его удобно реализовать на ЭВМ, учитывая ограниченность на их памяти, так как схема вычислений не требует выполнения обратного хода.

На первом шаге этого метода выберем ведущий элемент (перестановкой уравнений системы можно добиться того, чтобудет наибольшим по модулю коэффициентом при). Разделим первое уравнение системы на, во всех остальных уравнениях исключим, то есть сведем расширенную матрицы системы к виду

где

во втором шаге выберем ведущий элемент(можно сделать перестановку строк 2,…,n таким образом чтобы он был наибольшим по модулю). Разделим второе уравнение на, исключимиз всех уравнений кроме второго.

где

После n шагов получим матрицу

и численное значение неизвестных

Контроль вычислений можно осуществлять также, как и в схеме единственного деления, используя контрольные суммы.

Вычисление определителя и обратной матрицы метода Гаусса

В прямом ходе метода Гаусса над элементами матрицы А производятся элементарные преобразования, которые не изменяют определитель матрицы, кроме операции деления на ведущий элемент. Матрица преобразуется к треугольному виду с единичными диагональными элементами, ее определитель равен единице. Если в прямом ходе строки матрицы не переставляются то знак определителя не изменяется. Таким образом определитель не вырожденной матрицы системы равен произведению ведущих элементов в прямом ходе исключения Гаусса

.

Для его вычисления прямой ход метода Гаусса , как и при решении системы, только без преобразований вектора b. При решении линейной системы определитель можно вычислить попутно.

Если применяется метод исключения с выбором главного элемента, то в (13) необходимо добавить множитель, гдек – количество перестановок строк и столбцов.

Все вычислительные схемы метода Гаусса позволяют осуществлять одновременное решение систем линейных уравнений с различными правыми частямиПри этом количество вычислений увеличивается на преобразование новых столбцов правых частей, что дает значительную экономию времени счета.

В частности если вместо столбцов выбирать столбцы единичной матрицы порядкаn:

(1 на к-ом месте, остальные элементы – нули), к=1.2 , …, n, то решение системыбудетк-м столбцом обратной матрицы .

Таким образом для вычисления обратной матрицы требуется решить одновременно n систем уравнений с n неизвестными. Проводим последовательные исключения неизвестных в расширенной матрице

~после n шагов

~.

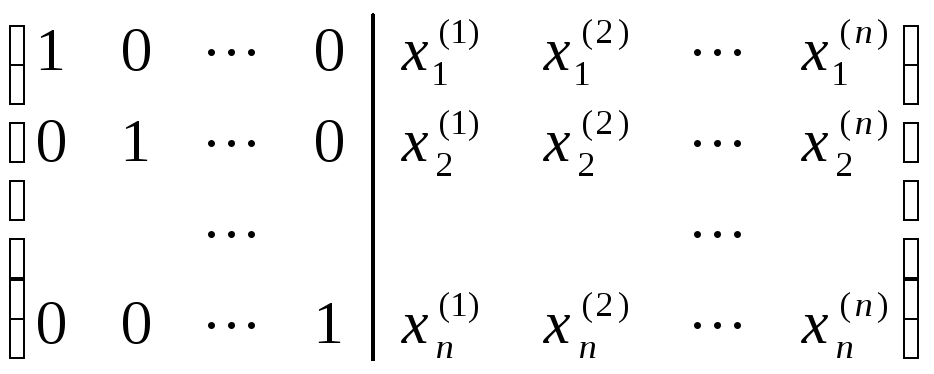Справа получим элементы обратной матрицы

.

Пример. Решить систему

методом Жордана-Гаусса.

Ответ,,.

Пример. Решить методом Гаусса-Жордана с выбором главного элемента системы

Ответ

.

Определитель равен .

Метод прогонки

Большинство технических задач сводится к решению систем линейных алгебраических уравнений, в которых матрицы содержат много нулевых элементов, а ненулевые элементы расположены по специальной структуре, например, ленточные квазитреуголные матрицы.

Задачи построения интерполяционных сплайнов, разностные методы решения краевых задач для дифференциальных уравнений сходится к решению системы алгебраических уравнений с трехдиагональной матрицей А. В матрице А все элементы не лежащие на главной диагонали и двух соседних диагоналях равны нулю. Такие системы можно записать

Выбор наибольшего элемента при исключении неизвестных методом Гаусса в таких системах делать нельзя, поскольку перестановка строк разрушает структуру матрицы. Наиболее часто к решению систем с трехдиагональной матрицей применяют метод прогонки, который является частным случаем метода Гаусса.

Прямой ход метода прогонки заключается в исключении элементов в системе (25). Так как, то первое уравнение системы имеет вид

.

Выразим через:и подставим во второе уравнение системы, получим уравнение связывающееии так далее. Пусть уже получено соотношение

Понизим в (26) индекс на единицу и подставим значение вi-е уравнение системы (25)

.

Отсюда

.

Сравнивая это выражение с (26) получим рекуррентные формулы для вычисления в прямом ходе:

.

Учитывая, что , полагаем. Обратный ход осуществляется по (26).

Почти во всех задачах, приводящих к решению системы (25) с трехдиагональной матрицей, обеспечивается условие преобладания диагональных элементов .

Это обеспечивает существование единичного решения и достаточно хорошую устойчивость метода прогонки относительно