Методы решения системы линейных алгебраических уравнений

1. Решение системы линейных алгебраических уравнений методом Крамера.

Многие задачи инженерной практики и вычислительной математики сводится к решению систем линейных уравнений. Эти задачи из области э/техники, р/электроники, механики, статистики, экономики, а также разностной аппроксимации дифференциальных и интегральных уравнений, локальной линеаризации систем нелинейных алгебраических уравнений и др.

Рассмотрим методы решения системы линейных алгебраических уравнений

АХ=В,

где - квадратная матрица порядкаn.

- векторы столбцов.

Если можно А системы не вырождены, то есть det, то такая система имеет единственное решение, которое может быть вычислено по формулам Крамера.

Алгоритм метода

1. находим определитель системы

.

Если то система имеет единое решение. Иначе система является не совместимой (не имеет решений), либо неопределенной (имеет бесконечное множество решений).

2. Находим определители

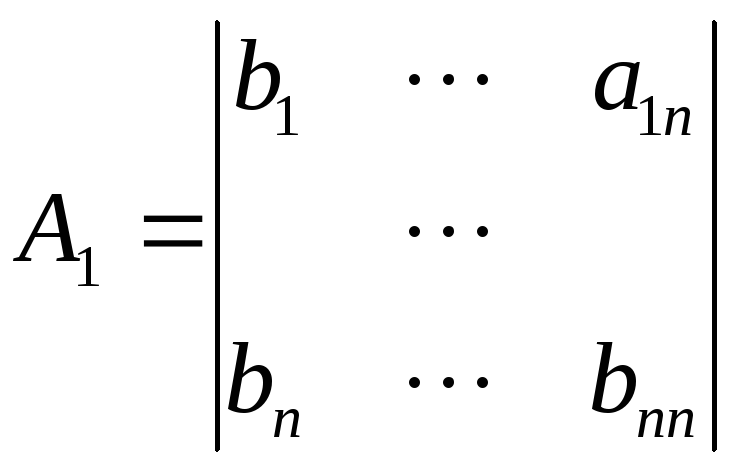
3. Находим решение системы по правилу Крамера

Пример. Решить систему уравнений

.

Систему уравнений по правилу Крамера при можно решить. Однако этот метод требует очень много других вычислений и поэтому мало эффективен. Для решения системы из 3-х уравнений требуется выполнить 51 операцию, а для системы из 5-и уравнений – 2885 операций(умножения и деления). И кроме того, значительно накапливается ошибка округления.

Метод Гаусса

Наиболее известным из точных методов решения системы является метод Гаусса. Идея метода состоит в том, что рассматриваемая система приводится к эквивалентной системес верхней треугольной матрицей (прямой ход). Из преобразованной таким образом системы неизвестные находятся последовательными подстановками, начиная с последнего уравнения преобразованной системы (обратный ход). Алгоритм Гаусса состоит из выполнения однотипных операций, которые легко программируются на современной ЭВМ. Однако точность результата и затрачиваемое на его получение время во многом зависит от организации вычислений. Существует много реализаций схемы Гаусса, дающих те или иные преимущества, в частности, есть схемы с заранее предписанным порядком исключения неизвестных, например, схема единственного деления, или же порядок исключения выбирают по ходу процесса (схема с выбором главного элемента).

Схема единственного деления. Считая (- ведущий элемент), делим первое уравнение системы (1) на

где

Затем исключаем из остальных уравнений системы вычитая изi-го уравнения первое, умноженное на соответствующий коэффициент . Приводи преобразованные таким образом уравнения

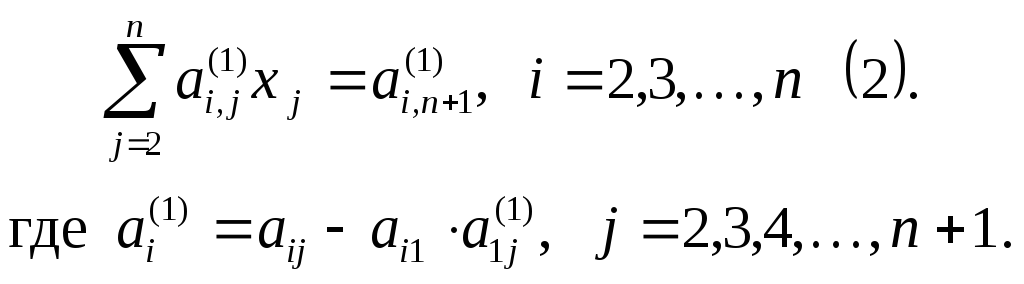
Неизвестное оказалось исключенным из всех уравнений, кроме первого. Далее предположив что, делим второе уравнение наи исключаем неизвестныеиз всех уравнений, начиная с третьего, и так далее до тех пор, пока не переберем все уравнения системы. После таких преобразований получим систему с верхней треугольной матрицей

.

Описанный прямой ход метода Гаусса реализуем в том случае, если ведущие элементы отличны от 0. Это условие будет выполнено, если отличные от нуля главные миноры матрицыА. Обратный ход метода Гаусса заключается в нахождении неизвестных из преобразованной системы (3). Значение определяется из последнего уравнения,из(n-1)-го уравнения и так далее.

количество операций умножения и деления вычисляется по формуле

При больших n в процессе решения системы желательно производить контроль вычислений. Для этого используются контрольные суммы

которые равны суммам элементов строк матрицы включая и свободные члены. Если над контрольными суммами в каждой строке проводить те же преобразования, что и над остальными элементами этой строки, то при отсутствии ошибок в вычислениях контрольные суммы должны быть равны суммам элементов соответствующих преобразованных строк расширенной матрицы.

Схема Холецкого

Решение системы линейных уравнений на МК можно выполнять в автоматизированном режиме только в случае небольшого числа уравнений, так как в памяти хранится элементов расширенной матрицы системы.

Больших n метод Гаусса реализуется в полуавтоматическом режиме, то есть строки преобразуются последовательно, а промежуточные результаты нужно записать в таблицу. В таких случаях удобно проводить гауссовы исключения по схеме Холецкого [Демир-г и Марон] позволяющей компактно записывать преобразованные элементы исходной матрицы и упростить программирование процесса вычислений.

В схеме Холецкого матрица системы А представляется в виде произведения двух треугольных матриц – нижний L и верхней U:

.

Такой алгоритм называют LU-разложением (Сичерский. Мат. аппарат инженера).

Элементы и вектор столбецy вычисляются по формулам:

преобразованная расширенная матрица системы имеет вид:

.

Порядок заполнения матрицы (10) следующий:

• Вычисляем элементы 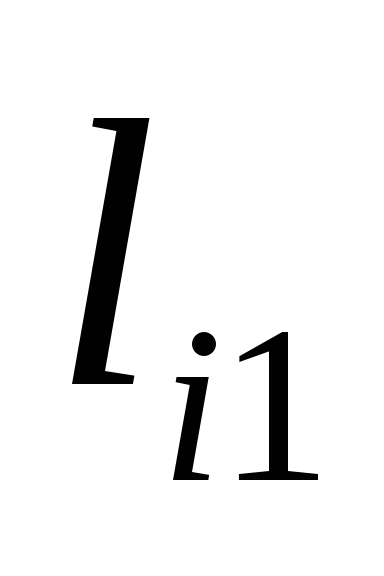1-го столбца (5);

• Вычисляем элементы 1-й строки (формулы (6));

• Вычисляем элементы 2-го столбца (формулы(7));

• Вычисляем элементы 2-й строки (формулы (8) и (9)) и так далее.

Заполняем всю матрицу в последовательности вектор-матрица.

LU-разложение позволяет представить систему (1) в виде , а векторх определить из последовательного решения системы

.

Прямой ход заключается в решению системы , то есть в заполнении матрицы (10) и получении элементов матрицыU и вектора y. При обратном ходе вектор х определяем из системы

.

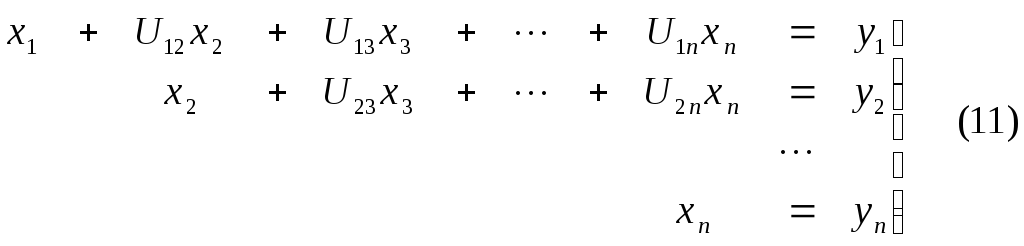Значение находится по формулам:

Вычисления по формулам 6 – 9 и 12 легко реализуется на МК.

Схема с выбором главного элемента

Если среди ведущих элементов окажется нулевой элемент, то перестановкой строк можно переместить нулевой элемент вк-й столбец на главную диагональ и продолжить вычисления. Если элемент близок к нулю, то деление на него уравнения приводит к большим по модулю преобразованным коэффициентам. В обратном ходе метода Гаусса на эти коэффициенты будет умножатся неточное значение неизвестного, что может привести к росту погрешности и потери точности.

Чтобы избежать существенного влияния вычислительной погрешности, изменяют метод Гаусса с частичным выбором главного элемента. В данном методе в качестве ведущего элемента на к-м шаге выбирают наибольший по модулю элемент в к-м столбце и перестановкой строк переводят его на главную диагональ.

В схеме Гаусса с выбором главного элемента ведущий (max по модулю) элемент находят среди всех элементов матрицы, и соответствующее ему значениеисключают из всех уравнений, среди коэффициентов которых еще не выбирались главные элементы.

Метод Гаусса с выбором главного элемента прост и численно устойчив для хорошо обусловленных линейных систем.