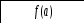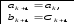7. Метод итераций

Изложенные в §4 методы приближенного вычисления корня – это методы итераций. Однако такое название принято давать более общему процессу , частным случаем которого является описанные методы.

Сущность метода и алгоритм

Рассмотрим уравнение (10). Пусть отрезок- отрезок, отделяющий корень х₀ этого уравнения, то есть . Выбираем определенную точкуи первым приближением назовем число С₁, где , по первому приближению строит второеи так далее.

.

Таким образом строится последовательность приближений . Если эта последовательность сходится, причем, то за конечное число итераций будет получено приближение С₀, представляющая приближение значений корня с данной точность , то есть. Однако итерационный процесс, определяемый формулой (11), не всегда сходящимся.

Выясним сначала геометрический смысл процесса и его сходимости. Корень уравнения (10) – это абсцисса х₀ точки пересечения прямой y=x и графика функции (рис), С₀ – произвольная точка на оси Ох; С₁ – абсцисса точки пересечения прямых (точка В₁).

По С₁ определяем С₂ как абсциссу точки пересечения прямых (точка В₂) и так далее.

На рис. последовательность точек сходится кХ₀.

Установим условие сходимости поскольку Х₀ – точное значение корня уравнения (10), то и, вычитая это тождество из (11) получим.

Применим к правой части равенства формулу конечных приращений Лагранжа , где, тогдаили. ПустьМ наибольшее значение тогдаи, (12) или(13) то, то есть C_n ближе к x₀, чем C_n-1. Покажем, что при выполнении условия (13) последовательность сходится кХ₀. Для этого будем последовательно использовать неравенство (12). Переходя к последнем соотношении к пределу прии учитывая, что, получаем, то есть.

На рис.1 представлен случай, когда и процесс сходится, на рис.2 – случай, когдаи процесс расходится.

Найдем оценку n-го приближения, то есть оценку . Применяя формулу (12), получим.

Отсюда (14).

Если , тои оценка приближенияC_n сводится к оценке модуля разности двух последовательных приближений.

Применим этот метод итераций к решению уравнения . Для этого запишем его в виде(15), гдеf – произвольный параметр. Уравнение (15), очевидно эквивалентно уравнению . Сравнивая уравнения (15) и (10), видим, что. Выбираем теперьf так, чтобы было выполнено условие сходимости (13)

.

Решая это неравенство, получаем, что при должно быть, а придолжно быть. Если функцияимеет на [a,b] ограниченную производную, то естьто при, а при. Выбратьf, удовлетворяющее этим неравенствам, обеспечиваем условие (13) сходимости процесса итераций для уравнения (15), а следовательно, и для исходного уравнения .

Пример. Уравнение преобразовать к виду, допускающему применение метода итераций. Корень отдален на отрезок [1,2].

Решение. Представим уравнение в виде . Тогда. Выберемтак, чтобыдля. Имеем, отсюда. Решая это неравенство получим. Так как на [1,2], то. Любое значение параметра , удовлетворяющее полученному неравенству, годится для применения метода итераций.

Алгоритм решения. Пусть на отрезке [a,b] отдален корень уравнения f(x)=0 и задано .

1. заменяем уравнение f(x)=0 на эквивалентное и выбираемf так, чтобы было выполнено условие . Выбрали.

2. Пусть определено (n-1)-e приближение C_n-1. Вычисляем f(C_n-1 )и определяем .

Оцениваем разность . Если, то процесс закончен и. Если же, то повторяем действие 2, заметивC_n-1 на C_n.

Замечание. Преобразование уравнения f(x)=0 к виду (15) для решения его методом итераций не всегда обязательно. Иногда уравнения f(x)=0 проще привести к виду (10), учитывая специфику конкретного уравнения и обеспечивая сходность итерационного процесса.

Так, например, уравнение x-sinx-1=0 можно представить в виде x=sinx+1, тогда и, если.

Случай алгебраического уравнения

Рассматривая до сих методы одинаково применимы как к алгебраическим уравнениям, так и к трансцендентным. Дополнительные предположение о том, что данное уравнение является алгебраическим, облегчит отделение корней.

Пусть уравнение f(x)=0 является алгебраическим уравнением n-ой степени и записано в виде f(x)=a₀x⁴+a₁x^n-1+…+a_n-1x+a_n=0 (1)

Как известно из курса алгебры, такое уравнение имеет ровно n-корней, если каждый корень считать столько раз, какова его кратность. Для уравнений (1) с действительными корнями, которыми мы ограничимся, обычно ставится задача отыскания всех корней, как действительных, так и комплексных.

Из теории Безу вытекает, что если является корнем уравнения, то то многочлен делится на. Поэтому разделив на многочленf(x) на двучлен , приведем к уравнению вида, где- частное от деления. Отсюда видно, что для отыскания следующего действительного корня уравнения (1) надо решить уравнениестепениn-1. Таким образом нужно найти все действительные корни уравнения (1). Деление многочлена на двучлен так и вычисление значений многочлена требуемых для методов приближенного отыскания корней, лучше производить по схеме Горнера.

Границы для корней уравнения (1) можно найти исходя из следующей теоремы.

Теорема: Если гдеА наибольшее из чисел , то (3).

Доказательство: Из (2) выводим , или, откуда(4).

С другой стороны

.

Из (2) следует . Поэтомуи, следовательно,(5). Сравнение неравенств (4) и (5) приводит к неравенству (3), которое и требовалось доказать.

Если x z является корнем уравнения (1), то должно иметь место равенство .

Поэтому значения х, удовлетворяющие неравенству (2), вследствие уравнение (3) корнями служить не могут. Итак, корни алгебраического уравнения (1) удовлетворяют неравенству или иначе, числослужит верхней границей модулей корней алгебраических уравнений.

Оценке (6) удовлетворяют модули всех корней уравнения как действительных, так и комплексных. Если речь идет только о действительных корнях, то можно получить значительно более точную оценку.

Пусть . Обозначим черезВ наибольшую из абсолютных величин отрицательных коэффициентов. тогда верхней границей положительных корней уравнения (1) служит число

(7)

к – номер первого отрицательного коэффициента.

Если к – верхняя граница положительных корней уравнения , (8) то число1/k будет служить нижней границей корней уравнения.

Пример. Рассмотрим алгебраическое уравнение .

Здесь . Правая часть неравенства (6) равна, тогда все корни этого уравнения по модулю не превосходят 8.

Первым отрицательным корнем является так чтоТогда верхняя граница положительных корней равна.

Для нахождения нижней границы составим уравнение (8), заменив х на ,после перемены знаков.

Здесь Верхняя граница положительных корней равна1+7/3 =3,33. Отсюда следует, что нижняя граница положительных корней первоначального уравнения 1/1,33=0,30.

Положительные корни уравнения, если они существуют, удовлетворяют неравенствам .

Для отыскания границ отрицательных корней заменим в данном уравнении х на –х.

Получим

или .

Здесь . Потому верхняя граница положительных корней ётого уравнения1+5/1=6.

Составим снова уравнение (8), найдем , что дает нижнюю границу корня уравнения с переменным знаком 0,46. Итак, окончательно, отрицательные корни исходного уравнения (если они существуют) находятся в границах.

Рассмотрим способ нахождения комплексных корней алгебраического уравнения с действительными коэффициентами.

Если таких корня, то произведение соответствующих линейных множителей дает,то есть квадратный трехчлен с действительными коэффициентами. Следовательно, для отыскания пары сопряженных комплексных корней достаточно выделить множитель вида.

Для выделения такого множителя можно воспользоваться схемой деления многочлена на квадратный трехчлен, аналогичной схеме Горнера.

Результат деления его на квадратный трехчлен можно записать в виде:

.

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях х, приходим к схеме

отсюда находим:

Нашей задачей является подбор таких значений p и q, при которых , тогда как при произвольно выбранныхp и q это условие не выполняется. Пусть выбраны некоторые значения p и q. Покажем, как выбрать поправки к этим значениям, чтобы уменьшить полученные значения b₃ и b₄.

Пусть новые значения коэффициентов будут . Не применяя вычисленных коэффициентов подставим эти значения в последние два уравнения (10). Тогда

Полагая и замечая, чтонаходим систему уравнений для отыскания поправок

с помощью которых находятся новые значения

Теперь можно пересчитать значения коэффициентов по формулам (10) и определить новые поправки из системы (11). Это делается до тех пор, пока коэффициенты b₃ и b₄ не станут пренебрежительно малыми по сравнению с остальными.

Укажем способ выбора первоначальных значений p и q. Если х по модулю невелико (меньше 1), то старшие степени малы по сравнению с младшими. Поэтому меньше по модулю корни могут приближаться корнями квадратного уравнения то есть в качестве начальных значений можно брать.

Наоборот, для больших младшие члены будут малы по сравнению со старшим и корня уравнения можно приближать парой корней квадратного уравнениято есть принимать в качестве исходных значений.

Вычисления располагают обычно в виде схемы, показанной в таблице 1.8. верхняя часть предназначена для нахождения коэффициентов, нижняя – для вычисления поправки.

Пример. Решим уравнение . Начальные значения выберемили, после округления,

Проделав три шага, остановимся на значениях Следующий шаг проделан лишь для проверки величины остатка и нахождения коэффициентов частного. Пренебрегая остатком, найдем, что заданное уравнение распадется на дваоткуда получаем четыре комплексных корняВ качестве заключительного контроля вычислим сумму и произведение всех корней, которые должны равнятьсяи(для нашего уравнения соответственно 2 и 15), подсчеты дают

Рассмотренный процесс нахождения поправок может оказаться расходящимся. Более устойчивым и быстрым является нахождение поправок из аналогичной схемы

где коэффициенты получаются по формулам

схема вычисления по аналогичным таблицам, добавив несколько столбцов для нахождения коэффициентов .

нет

да

нет

да

да

нет