Экстраполяция

Процесс нахождения значения функции по формулам интерполяции в точках принадлежащих отрезку [a,b] называется интерполяцией , если то называется экстрополяцией.

Рисунок.

Для экстрополяции можно использовать те же интерполяционные формулы Ньютона и Логранжа, если определяется значение функции f(x) в точке x<а, то следует применить первую интерполяционную формулу Ньютона, которая называется экстрополирование назад. При нахождении точки x>b , то следует применять вторую системную формулу Ньютона, которая называется экстрополирование вперед. Однако при использовании экстрополяции при удалении точек от отрезка погрешность вычисления резко возрастает.

Обратная интерполяция

Рассмотренные ранее задачи заключались в нахождении функции по соответствующему значению аргумента. Зачастую необходимо решить обратную задачу, когда по заданным функциям нужно найти значение аргумента, отсутствующих в таблице:

				…
				…

Для решения данной задачи используется обратная интерполяция, то есть, считаем, что значение функции , а аргумент. При этом значения функции будут не равноотстоящие, поэтому следует использовать формулу Лагранжа, либо формулы Ньютона при не равноотстоящих узлах.

Приближение функций

Интерполяция .Постановка задачи. Задача интерполяция заключается в следующем: пусть на отрезке ,точкеn+1,задана функцияf(x) своими значениями:

Необходимо определить значение функции в любой точке .По другому задача интерполяцияf(x) заключается в том чтобы построить функцию F(x) принадлежащую определенному классу функций ,и принимающая значения в заданных точках:

точки называются узлами или полосами интерполяции, аF(x) – называется интерполирующей. Обычно интерполирующую функцию пишут среди многочленов степень которой не превышаетn и которая удовлетворяется следующими условиями:

Доказано ,что условиям (1) многочлен степени n . И задача интерполяция заключается в нахождении выражения , алгебраического полинома . Геометрический смысл интерполирования заключается в замене кривойf(x) интерполируем многочленом.

Рисунок.

В многочленных приложениях в основном решается две задачи интерполяция :

3. вычислить значения функций f(x) в точках совпадающих с узлами интерполяции , сравнительно простыми средствами.

4. найти аналитическое выражение полинома в тех случаях, когда функцияf(x) задана таблично, либо очень сложным выражением.

Интерполирующий многочлен Лагранжа

Выберем в качестве интерполирующей функции F(x) , полином так, чтобы он в узлах интерполяции совпадал со значениями исходной функции,

Для этого

многочлены в степени построены следующим образом:

отсутствует тот член, который указан в скобке при

Не трудно заметить, что при ;первой многочлен равняется единице , тогдаможно записать:

Этот полином называется интерполяционным многочленом Лагранжа , а многочленыназываются коэффициентами Лагранжа.

Рассмотрим частные случаи интерполяционной формулы Лагранжа:

1. n=1,тогда

n=2, тогда

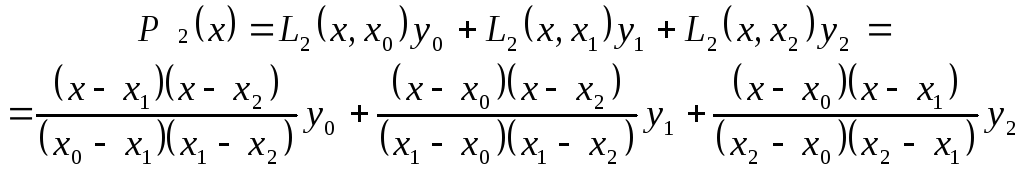
При использовании интерполяционных формул значение исходной функции f(x) и интерполяционного многочлена в точке X не совпадающих с узлами интерполяции не равны друг другу. Обозначим это различие как , эта разность определяет погрешность интерполирования. Из теории вычисляемых методов можно определить оценку , если функцияf(x) имеет непрерывную (n+1) производную в точке тогда,

где - максимальная-я производная.

Интерполяционный многочлен Лагранжа можно использовать в тех случаях, когда ведется многократное интерполяционное различие функций, при одних и тех же узлах интерполяции. В данном случае можно заранее вычислить коэффициенты Лагранжа, так как они не зависят от f(x) , кроме того узлы могут быть разноотстоящие (с разным промежутком), однако если для улучшения приближения функций необходимо добавить хотя бы один узел, все коэффициенты Лагранжа необходимо вычислять снова.

Интерполяционные многочлены Ньютона

Конечные разности. Пусть f(x) задана на ,;

Пусть узлы интерполяции будут равноотстоящими:

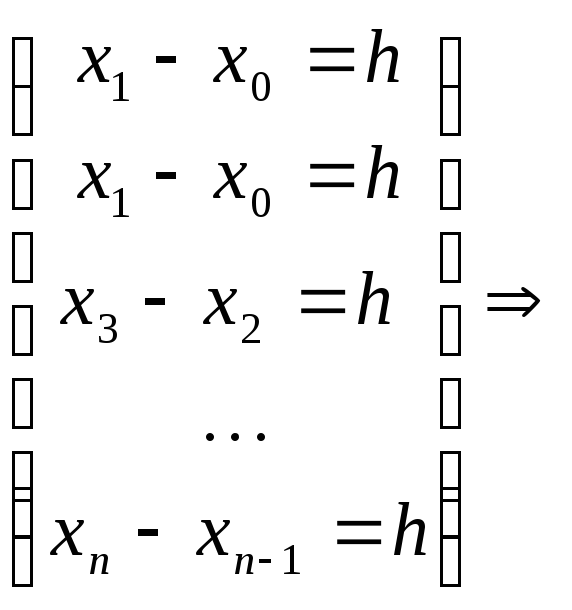
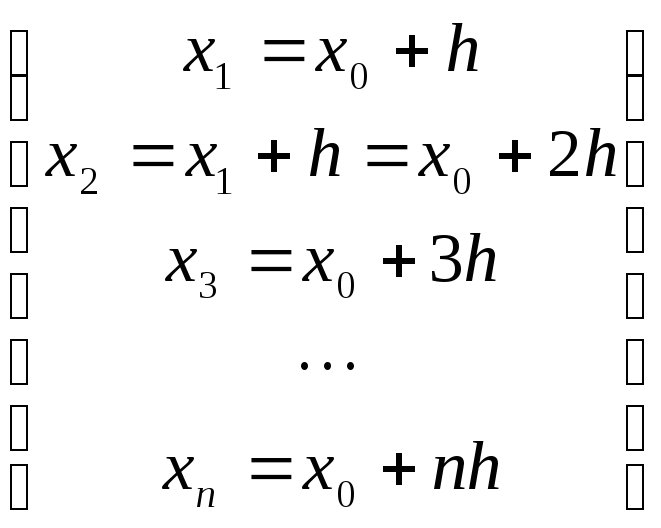
эти разности называются конечные разности первого порядка.

-разности к-того порядка.

Эти разности используются в интерполяционных функциях Ньютона , а также при численном дифференцировании.

Первая интерполяция формула Ньютона.

Пусть необходимо интерполировать функцию f(x) , которая задана своими значениями в узлах интерполяции

Представим интерполяционный многочлен:

Определим коэффициенты этого многочлена так, чтобы в узлах интерполяции исходная функция совпадала с интерполяцией

Пусть

.

Пусть

;

Пусть

Пусть

Отсюда общий вид подставимви получим первую интерполяционную формулу Ньютона интерполяция вперед

Эта формула применяется в тех случаях, когда необходимо найти значения функции в начале отрезка интерполирования. Преимуществом этой формулы, перед формулой Лагранжа в том, что в формуле Ньютона в знаменателе стоит к!, это обозначает, что с ростом к коэффициенты убывают, то есть с определенного члена остальными можно пренебречь, кроме того, для увеличения точности приближения, при добавлении нового узла интерполяции, в полиноме добавляются еще одно слагаемое.

Рассмотрим частные случаи:

Из теории приближенных вычислений получилась формула погрешности интерполирования первой формулы Ньютона:

производная исходной функции f(x) любой точке отрезка интерполирования.

Часто пользуются другой формулой для вычисления ,когда n+1производная не известная , но есть узел интерполяции , тогда :

Так при линейной интерполяции погрешность интерполирования:

Данную формулу следует использовать для нахождения значения функции в начале отрезка интерполирования Рисунок.

Пусть исходная функция f(x) задана своими значениями в n+1 точках, т.е. в узлах интерполирования: то есть

Искомый полином будем искать в следующем виде:

Определим коэффициенты этого полинома исходя из этих условий. Пусть

Пусть ;

Пусть

С учетом найденных коэффициентов полученная формула приобретает следующий вид:

Это вторая интерполяционная формула Ньютона или формула интерполяция назад. Ее следует использовать при нахождении значений функции в конце отрезка интерполирования, то есть когда x близко к . В середине отрезка две формулы Ньютона равноценны.

Пусть

С учетом этого вторая формула Ньютона приобретает следующий вид:

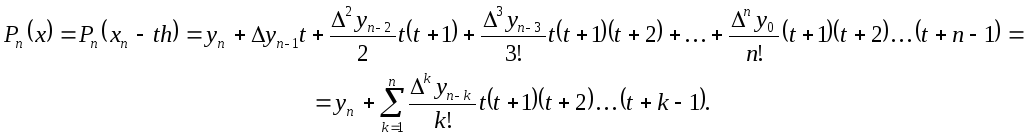
Для оценки погрешностей вычисления для второй интерполяционной формулы Ньютона:

При наличии разности применяется следующая формула:

формулы Ньютона следует использовать, когда отрезки интерполяции одинаковые, т. е. при равноотстоящих узлах, если узлы не равноотстоящие, следует применять формулу Лагранжа, либо специальные интерполяционные формулы Ньютона с использованием раздельных разностей.