2.1. Классификация распределительных задач

Распределительные задачи по наличию того или иного признака можно. делить:

1. Пв виду целевой функции на линейные и нелинейные. Если затраты (до-), определяемые объемом xcj 'ресурса (', выделенного на выполнение рабо-;, равны XijCij и ограничения линейны, то 'имеем линейную распределитель-> задачу (в противном случае—нелинейную).

2. По имеющемся в наличии потребным ресурсам на сбалансированные крытые) и несбалансированные (открытые). Если общий объем наличных ре-

'" / . п --.

сов ^ и, равен общей потребности в них zj d,, то имеет место сбаланси-;

'•=1 . /=i ; • анная (закрытая) распределительная задача

т п ^b,^dr. 1=1 i=i

Д " . .' • ^и же 2j Ь» ^ zj dj, то задача называется несбалансированной (открытой) и <=1 /=i .

. 35

требуется не только распределить ресурсы по работам, но и решить т акэ)

(т " \ I

работы вообще не выполнять если ^ &» < 2j ^/ •^пи00 какие ресурс «=1 /=i 7 ':

( ^т " \ 1 пользовать I если ^ bj > ^ dj \ •

\ 1=1 /=l / ^ 3. По характеру изменения переменных на три класса: •|

1) если все переменные при решении могут иметь любое значение "в, сти допустимых, имеющих непрерывный -характер, то такие задачи шб относить к классу задач с непрерывным изменением переменных; •';

2) если на все переменные или на их часть наложено дополнитель бовавие целочисленности, то мы 'имеем дело с целочисленными 'распред нымя задачами; . ' ;

3) если -областью допустимых изменений каждой переменной явлй множество целых неотрицательных чисел, а некоторое заданное конечд жество (например, количество единиц продукции разных видов), то дискретную задачу 'распределения, л

4. По количеству экстремумов у целевой функции на одноэкстрема многоэкстремальные. I

Класс распределительных задач, для которых любой локальный i целевой функции на множестве допустимых планов является одновр.е глобальным оптимумом, называется одноэкстремальным. При наличии i многих локальных экстремумов задачи называются многоэкстремальнывд

5. По характеру распределения ресурсов во времени на статические мические.

Если распределительная задача не связана со временем или каждо! дующее распределение не зависит от всех остальных .распределений, за! зывается статической, в противном случае—динамической. . -1

2.2. Задача о назначении

Задача о назначении в общем виде формулируется так.' >. Пусть имеются п работ и п кандидатов для выполнения э| бот. Назначение кандидата i на работу / связано с зат] ^c^i(i, /=1> 2, ..., п). Требуется'найти назначения кандида все работы, дающие минимальные суммарные затраты: пр| каждого кандидата можно назначить только на одну ра| каждая работа может быть занята только одним кандидате

Это типичная экстремальная задача комбинаторного ви решение путем прямого перебора практически невозмож! сколько-нибудь больших л, так как число перестановок N. =1Х2ХЗХ...Х {п-\)п. ;

Рассмотрим на конкретном примере основные этапы ;

ционного исследования задачи о назначении, л

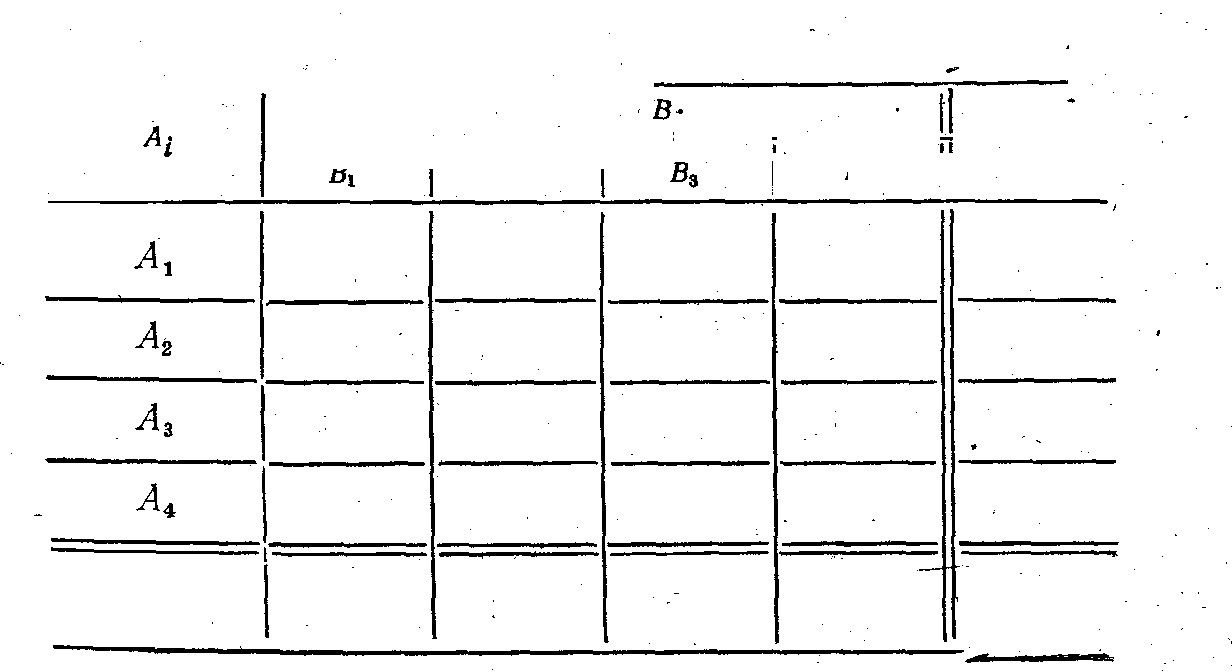
Постановка задачи и выбор критерия оптимизации. Пус' монтажа четырех объектов (п=4) требуется четыре крана ^ Из отчетных данных известно, какое время необходимо ка;

крану Ai для монтажа объекта В/. 'I

Нужно так распределить краны по объектам, чтобы cyj ное время на монтаж этих объектов было минимально. В ;

случае сц—это затраты времени Л,-го крана при монтаже та В,. Исходные данные представлены в табл. 2.1.

36 ^

Выявление основных особенностей, взаимосвязей и количест-»енных закономерностей. Введем переменные Хц(1, ;'=!, 2, ..., я), щеющие следующий смысл:

{1, если Л;-й кран распределяется на объект В;

' -^Ч ⁼⁼ п ~

U в противном случае.

'ак как каждый кран можно распределить (назначить) только на дин объект и на каждом объекте может работать только один ран, то введенные переменные х.ц должны подчиняться двум усло-иям: -

п=4

3 ^•==^„+^2+^з+-^«4=¹ для всех г=1, 2,..., 4;

/=i

n=4

3 Xi/ = x,, -4- x,} + x„ 4- х^, -= 1 для всех /• = 1, 2,..., 4- . ;=i

Построение математической модели. Критерий оптимизации — уммарное время монтажа четырех объектов У—математически южно записать так:

4 4

^у = P.i^n + • • • + Ci,X„ + ... + С„Х„ = S S ^c^'•^•• . <=1/=1

аким образом, задача свелась к нахождению таких чисел хц, ко-орые удовлетворяют двум вышеприведенным условиям и миними-ируют суммарное время монтажа.

Исследование математической модели. Для решения задачи назначении имеется несколько методов, среди которых наиболь-юе^аспространение нашел венгерский метод. Основной принцип

оптимальность решения задачи о назначении — не нарушает-' при уменьшении (увеличении) элементов строки (столбца) на дну и ту же величину di(dj). Решение считается оптимальным,

если все измененные искусственно затраты С(/^0((, /'==1, 2, .J

4 4 ; If

я можно отыскать такой набор Хц, чтоУ==3 S ^c'ii^xii⁼⁼Q• -Ц

'^=1/=11 Я Алгоритм метода включает следующие основные этапы: Г

1) получение нулей в каждой строке, для чего найти накг ший элемент в каждой строке с?< (табл. 2.1) и вычесть его из|| ее элементов, получаем новую матрицу (табл. 2.2), ан алогично «|И ется для каждого столбца (табл. 2.3): • - . Я

2) поиск оптимального решениям. Для поиска оптимально^ шения необходимо рассмотреть сначала одну из строк таб.Д имеющую меньше нулей. Отметить точкой один из нулейдИ строки и зачеркнуть все остальные нули этой строки и того с|я вда, в которых находится этот нуль. Аналогичные операции f довательно проводят для всех строк. Если назначения, ко|н Еолучены при всех нулях, отмеченных точкой, являются по-ЦД ^т. е. число нулей, отмеченных точкой, равно п), то решение^И ется оптимальным, в противном случае следует переходить |в дующему этапу; • Я

3) поиск минимального набора строк и столбцов, содерз^Я иули. Для этого необходимо отметить точкой: |И

1-Г' , f\ Г\ Л^И

v gge строки, в которых не имеется ни одного отмеченного .точ-

й нуля (строка 4 табл. 2.3); .

б) все столбцы, содержащие перечеркнутый нуль, хотя бы в од-,й из отмеченных точкой строк (столб. 3 табл. 2.3);

в) все строки, содержащие отмеченные точкой нули, хотя бы одном из отмеченных точкой столбцов (строка 3 табл. 2.3).

Таблица 2.4

Действия б) и в) повторяются поочередно до тех^пор, пока -есть •о отмечать. После этого необходимо зачеркнуть каждую непоме-нную строку и каждый помеченный столбец (цель"этого этапа— ювести минимальное число горизонтальных и вертикальных пря->ix, пересекающих, по крайней мере, один раз все нули); •

4) перестановка некоторых нулей. Взять наименьшее число из х клеток, через которые не проведены прямые (в табл. 2.3 это ело 2). Вычесть его из каждого числа невычеркнутых столбцов

прибавить к каждому числу вычеркнутых строк. Получим бл. 2.4.

Эта операция не изменяет оптимального решения, после чего сь цикл расчета начинается с этапа 2ц продолжается до получе-:я оптимального решения. В нашем случае число нулей, отмечен-ix точкой, оказалось равным 4, значит, назначение является пол-im, а решение—оптимальным. Клетки, отмеченные точкой, ук-а-[вают объект монтажа для каждого крана.'

Оптимальное решение может быть не единственным. Для на- -;й задачи минимальное значение целевой функции будет равно

=Cll+C22+C33+C44==3+4+2+8==17.

2.3. Транспортная задача

Транспортная задача в общем виде формулируется так. Пусть имеется т пунктов отправления (или пунктов гороизвод-

•тва) -4i, As, ..., Am и п пунктов назначения (или пунктов потреб-1ения) Bi, В2, . • •; Вп. Обозначим ресурсы груза в t-м пункте от-шавления через a,(i=l, .... от), а потребность каждого /-го пункта ютребления через Ь,{]=\, 2, ..., я). Заданы стоимости перевозке

•диницы груза от каждого 1-го пункта отправления до каждого

•го пункта назначения. Требуется определить, какое количестве 'руза хц^О необходимо перевезти из каждого 1-го пункта отгарав-юния до каждого /-го пункта назначения, чтобы:

1) вывести грузы всех поставщиков;

2) удовлетворить всех потребителей; ':....•

3) достигнуть экстремума целевой функции.

Рассмотрим на конкретном примере основные этапы оперЭДйой-юго исследования транспортной задачи.

Постановка задачи и выбор критерия оптимизации. Пусть в го-юде N имется четыре домостроительных комбината (ДСК) Л[, is, аз, Л4 и пусть строятся четыре микрорайона В\, Вч, Вз, В^ Известны производственные мощности домостроительных комбина-

•ов и потребность в комплектах унифицированных изделий каж-юго микрорайона. Ресурсы отправителей и ресурсы потребителей 1звестны (табл. 2.6). Известны также приведенные затраты, свя-

Таблица 2.6

————————————————————.—

л, ————————————1———————Н————

_____ - В, 1 В, 1 Вз | В, .. || о;

Л, 70 38 24 92 14 Ла . 58 18 56 , 72 20 Лз 19 10 100. 30. 26 At 3 36- 121 '8 41 . •

Ь/ 30 • 22 15 '34 ^- ,

эанные с доставкой одного комплекта унифицированных йжелий из каждого пункта отправления а каждый кункт назначения.. Тре­буется так распределить продукцию домостроительных комб-янатов "о строящимся микрорайонам, чтобы йуммарные приведенные за< траты, связанные с доставкой всего груза от отправители к потре-

, ^

бителю, были минимальны. Обозначения оставим такими жё| при формулировке транспортной задачи в общем виде (см. вй

Обозначим: a.i, bf—число комплектов унифицированных.;

лий соответственно, выпускаемых (ресурс'отправителя) (-m | и потребляемых /'-м микрорайоном; хц—число комплектов г поставляемых i'-м ДСК У-му микрорайону. •

Выявление основных особенностей, взаимосвязей и количес' ных закономерностей. Предположим, что общий объем произв(

т п

ва равен общему объему потребления 2 ^at:=S bj(fn=4, п=

i=i /=i .это сбалансированная (закрытая) траспортная задача, в прс иом случае—несбалансированная (еткрытая). ^

Чтобы вывезти грузы всех н@ставщик»в, необходимо выпо вне равенств ^;

п '"

3 Хц==а, ((=1, 2,..., т). ;

Чтобы удовлетворить всех потребителей, необходимо выпй вие равенств ^;

т . • „•

' . S^-/^/- О ==1.2,....л). j

Построение математической модели. Критерий оптимизаод суммарные приведенные затраты на доставку всего груза отпр| теля потребителю— i

т п •

У=с„х„+.--+с^,/+...+^^„=3 S ^с'/^-

1=4=1 ,

Таким образом, задача свелась к нахождению таких значений ej менных, которые удовлетворяют двум вышеприведенным равб вам и минимизируют,суммарные приведенные затраты на дос ку груза отправителя потребителю. . |

Исследование математической модели (оптимизация). Иссж вание и решение транспортной задачи, как правило, провода в два этапа. На .первом этапе находят какое-нибудь (хотя бы. удачное) решение, далекое от оптимального, но удовлетворяю совокупности линейных равенств (ограничений), или убеждай в том, что такого решения не существует. Этот.этап называв отысканием опорного (начального) плана. , i|

На втором этапе производится последовательное улучше этого плана по определенным правилам до тех пор, пока даль! рее улучшение станет невозможным. От того, каким будет oi вый план, зависит время решения транспортной задачи на вто| этапе решения. В настоящее время существует много способов Строения опорного плана. Рассмотрим наиболее эффективй В качестве исходных данных для построения опорных пла используем данные табл. 2.6. ^

W •'

Способ аппроксимации Фогеля. В большинстве случаев этот спо-• дает опорный план, самый близкий к оптимальному. Поэтому ' рекомендуют использовать при расчетах вручную по матрицам

1ЫИОГО размера. ,., * В основе способа аппроксимации Фогеля лежит концепция

пайов взимаемых за выбор не самого оптимального с точки >ния транспортных издержек маршрута. Штраф по каждой юке и каждому столбцу определяется из анализа маршрутов различными показателями издержек (как разность двух различ-х уровней транспортных издержек). Первой заполняется клетка трицы (таблицы), в которой фиксируется самый крупный раф. После заполнения клетки штрафы пересчитываются и так тех пор, пока все ресурсы не будут распределены. Алгоритм метода включает следующие основные этапы:

1) вычисление разностей в каждой строке и в каждом столбце ^трицы (табл. 2.7) между наименьшей стоимостью и ближайшей ней по величине. Разности по строкам записываются справа столбце разностей, разности по столбцам—внизу в строке раз-

^>стеи- Например, для строк Ai разность равна AiB^—AiB3=38— -<-4==14 и т. д •

0\ '"'ч .,-.--,.-

^) поиск из всех разностей как по строкам, так и по столбцам, финальной. В нашем примере максимальная разность раина 38. находится в строке Ла. Обведем максимальную разность рамкой;

AF;

3) размещение в клетку, где находится наименьшая сг^Н А^Вч= 18 (строка с наибольшей разностью), максималб1^Ш ложного количества, ресурсов. Оно равно 20, т. е. всему з^Н ресурса отправителя Ла. Поскольку все ресурсы отправ^^И исчерпаны, строку Ач исключаем 'из дальнейших расчетов, 1^И го отметим все клетки этой строки точками; |^1

4) вычисление разностей по столбцам и строкам, не пр^И во внимание стоимости в клетках, имеющих ресурсы, и ^^И с точкой (исключенную строку или столбец), и определен!^Л симальной разности в строке или столбце (5з==76); |Н

5) поиск минимального элемента в строке или столбце!'!^ симальной разностью А \В^-== 24 и размещение в данную ,^В максимально возможного количества ресурса, "возвращением пу 4) и т. д. • . '^И

Окончательно целевая функция ' . Щ

У=23-19+7 -3+20 •18+2.10+14- 24+ Я • +1-100+34 •8=1546. •

В качестве опорного (начального) плана для решения |Н .возьмем опорный план, найденный способом аппроксимациям ля, который иногда называют приближенным способом р^Н транспортных задач (см. табл. 2.7). После этого .переходимыми рому этапу решения транспортной задачи. ;Г

Как указывалось ранее, на втором этапе решения трансл|И задачи производится последовательное улучшение опорногоГ В настоящее время существует несколько методов последо^Д ного улучшения опорного плана, например распределительной тод, метод потенциалов, метод stepping-stone. Основой выЩ тельного процесса (алгоритма) этих методов является опредцД критерия оптимальности -^И

6ij=^Cij——Zij, ''^1

где Cij—затраты, связанные с доставкой одной единицы рдИ (в нашем примере одного комплекта унифицированных из|И из 1-го пункта отправления (г-го ДСК) в j-й пункт назн^В (/'-и микрорайон); г,, — расчетные затраты, связанные с досвИ одной единицы ресурса из 1-го пункта отправления в /-йЦ назначения, определяемые для тех клеток опорного плана, р^Н в которые не распределены. Ц Если все 6,7^0, то данный опорный план оптимальныйД нет, то с помощью этого критерия оптимальности можно учЩ способ улучшения этого плана. Рассмотрим метод потенциалов Алгоритм метода включает следующие основные этапы: Ц 1) составление и решение системы уравнений ,Ц

V,—Ui=Ci„ Я

где у,, Ui—некоторые переменные, использующие те индексыД на пересечении которых в соответствующих клетках распред|Д

46 . ' • , ' • . ^ 'Я

урсы. Для нашей задачи: . ,

-^г Uз—^ul^=cl^з=—^r' Uz—«2=^22= 18;

^; Vl—^Uз==^CЭl⁼⁼^^;

U2—MЗ==C32==^:Ю;

Vl—M4=^C41=⁼3; .

t»s—uз=^:Cзз==100;

Vt—U4==C44^::=8.

Имеем семь уравнений и вос^^вес^х. ^^^

неизвестных, ^^.^^^^зн^^^^^^^ как правило, для .равнениях, дается произ^л^ное^ ^^ „^ний наибв-

легчения счета, равное нулю. п_ Положим из=0.

^{тлутаем:}

2) определение значения гц:

Zif=Vj—Ui.

S^X^^^^^^^

z„=ui-ui==19-76=-57-,

^^-и,=\0-76=-^'' ^=t,4-ui=24-76=-52;

^i==ui-U2=19+8=27;

, ^з=Уз-"2=100+8=108;

224=У4-"2=24+8=32;

Z34=U4-"3=24+0=24; - •

Z42=U2-"4==10-16=-6; ,

24з=Уз-»4=100-16=84;

3) определение значения оц:

Oij==Cij—Zij .

проверка условий оптимальности^ все ^^ то и^одн^и лан оптимален. Если некоторые 6„<U, то перелиА

порному плану: 7n_L^7—127-8ц=сц—2ц==70+57—12/,

6i2-Cl2-Zl2=38+66=104;

6^ci4-2i4=92+52==144; ;

8^==c2i-Z2i==58-27=31; • _ б2з=С2з-223=56-108=-52; -, ^

; б24='С24— 224=72—32=40; - ' | бз4==Сз4—2;34=30——24==6; ' | 642==C42—Z42==36+6=42; '| б43=С43— 243=121—— 84=37. ]

В нашем случае б2з<0—переходим к новому опорному п|

4) построение нового опорного плана, которому отвечав! шее-значение целевой функции, для чего в опорный план ы та переменная хц, которой отвечает наименьшее отрицателы чение б;/. Вводя новую переменную, одновременно изменяют переменные по меньшей мере в трех заполненных клетках, не нарушались итоговые значения в строках и столбцах та( Для этого строят многоугольник, в котором одна из верщ

Таблица Z.8 Таблица 2.9 :

- -' Вг bj + ______^ А

-. \.18 \. 56 •\ 18 N. 5В А? \ \ ^А! \. •S,

²⁰ \ 1 \ '⁹ ^^ ¹ ^\

\ ' 10 М wo ^\ю '\ wo '

^AJ \. _i\ ^А3 \ \

г \- -' i -\ з '\ о \. i

+. I—ч———^" *————•^•-—————

' — ~ Вг Вз ^

ходится в свободной клетке, для которой 6,/<0, и имеет на! шее значение, а остальные — в заполненных ресурсами ( женных); при этом все углы многоугольника^ должны! прямыми (многоугольник,^ отмеченный пунктирной з в табл. 2.7). В пределах клеток, лежащих в вершинах много ника (табл. 2.8), производят перемещение ресурсов. Если дд бодной клетки поставить знак «+», а в следующей вершине затем «+» и так далее, поочередно изменяя знак, то в своб клетку переносится меньшее из чисел, стоящих в клетках с о -тельными знаками. В результате она исключается из опорно зиса как базисная переменная. Одновременно необходимо у< вить равновесие по всему многоугольнику, j

При использовании правила перераспределения ресурсов делах многоугольника, распределение ресурсов примет' табл. 2.9.

При этом сумма ресурсов по всем строкам и столбцам ост без изменения. Проводя соответствующие изменения в исх< опорном плане, окончательно получаем новый опорный (табл. 2.10). J

Суммарные затраты на доставку продукции составят У= Х24+19-18+1-56+23-19+3-10+7-3+34-8.=1494 руб., что з тельно меньше, чем при исходном опорном плане, определи

48-' . ^\ • i

способом аппроксимации Фогеля. По сравнению с исходным опор­ным планом, который представляется на первый взгляд также ра­зумным, суммарная величина затрат -на доставку продукции уменьшилась примерно на 3,3%.

ГпК»„„п 1 1П

Нахождением нового опорного плана заканчивается, как говорят (атематики, первое приближение (первая итерация). Дальше ана-югичные операции повторяются, но уже для нового опорного пла-а. Последующие вычисления показывают, что все Si/^O, т. е. порный план, полученный в табл. 2.10, является оптимальным. Критерию оптимальности б,/ и переменным щ и и,- можно придать кономический смысл.

Введем условные цены-оценки для каждого вида ресурса отпра-ителя и потребителя, присвоив их соответственно переменным и,. i=l, ..., m) и vj(j=\, ..., п). Эти оценки, или, как их чаще на-мвают, потенциалы, выступают в задаче как локальные (пояс-ые) цены (или наценки к единой цене), создающие заинтересован->сть в правильном направлении перевозок. При этом критерий пимальности выражает следующее: если какая-то перевозка осу-ествляется, то цена в пункте потребления равна цене в пункте травления плюс транспортные затраты, т. е. 6ц==0 и у/ = ы,+с</.

остальных случаях цена и, не может быть больше, чем щ+с„, ж.как ресурс в пункте б] по такой цене можно было, бы полу-">, привезя его с затратами сц из пункта Л,. Следовательно, • ',,^uiГcч^ ^т- ^е- в обоих указанных случаях разность цен не пре-^ шает затрат по перевозке и критерий оптимальности бг/^0. Час-

-^и """Роении опорного плана или в процессе решения задач» Рсь^ ^{потенциалов} число клеток, в которые распределены ре-

td(-w'> ^{меньше от}+^/г~^l^ ГО⁶ /"—число пунктов отправления ут); п -— число пунктов потребления (столбцов). В этой ситуа-

"³²⁴⁰ 49

ции говорят, что имеет место вырождение. Для устранения вы«Г дения применяют несколько способов: - U

1) вводят в некоторые свободные клетки ресурсы, ра)Щ нулю, и данные клетки считают занятыми местами; 'J

2) выбирают несколько клеток, дополняющих сумму заи^Н клеток до т-\-п—1, вводят в них сколь угодно малые объемйЦ ревозок. • '. • |я

2.4. Общ^я линейная распределительная задача f

Рассмотрим на конкретном примере основные этапы orf ционного исследования общей линейной распределительной|Д Дачи. ' . 1я Постановка задачи и выбор критерия оптимизации. Пусть if , торое предприятие может изготавливать изделия четырех вД mi, Яа, Из, И^. Известно, что .для изготовления изделия требуД три вида оборудования: Oi, О-г, Оз- Известно также, сколько, Щ мени потребуется на изготовление каждого изделия на кадД оборудовании, фонд времени работы оборудования (сколько|Д мени может проработать каждое оборудование) и какая при|Я может быть получена при реализации • каждого ' изд|Н /табл. 2.1 П. . " Я

Необходимо так распределить изделия по оборудования!» <5ы предприятие имело максимальную прибыль. Исходные д1 для расчета сведены в табл. 2.11. Обозначим: bi—ресурсы о дования О»; ai, — время изготовления /-го изделия И, на 1-м| рудовании; ci—прибыль от одного изделия Я/; х/—колич j-x изделий, которое необходимо выпустить на предприятии. *

Выявление основных особенностей, взаимосвязей и количес ных закономерностей. Зная ресурсы оборудования и время, а чиваемое каждым оборудованием на изготовление каждого' дия, можно записать следующую систему неравенств: ' 1

Зх1+5х2+2хз+7х4й$ 15; - | 4xi+3x2+3x3+5x4S£9; | 5xi+6x2+4x3+8x4sS30 •I

а виде системы равенств, если в каждое из неравенств ввести фик­тивные изделия (дополнительные неизвестные) х&,- Хв, x^, исполь^ зуюшие оставшийся ipecypc оборудования. При этом время изго­товления их на соответствующем оборудовании принимается рав­ным:

Ql5==l; Я25==0; аз5==0; 016=0; Й26=1;

йзб=0; ai7=0; 027==0; аз7===1. Тогда система равенств запишется в таком виде:

ЗХ1+5Х2+2Хз+7Х4+1Х5+ОХб+ОХ7=15;

4х1+Зх2+Зхз+5х4+Ох5+1'Хб+Ох7=9; (2.1>

5Х1+6Х2+4Хз+8Х4+бх5+ОХв+1Х7=30.

Это преобразование производится с целью упрощения вычисли-гельной процедуры в дальнейшем. • '

Кроме того, следует ввести дополнительное ограничение исходя i3 реальности задачи. Все неизвестные задачи могут быть равнь» 1ли больше нуля (т. е. неотрицательны):

х,^0 (/=1. 2, ..,, 7). ^] . (2.2)

Построение математической модели. Критерий оптимизации — ;уммарную величину прибыли для предприятия можно записать '.ак: ' '

7 . •

У=с,л,+...+с^.+...+с^==3^- . (²-³) /=i

Значения прибыли cs, Св, cj принимаем равными нулю. Таким •бразом, задача распределения продукции по оборудованиям све-ась к нахождению таких значений Переменных д:/(/==1, ..., 4), оторые удовлетворяют системе равенств (2.1), дополнительным граничениям (2.2) и максимизируют прибыль предприятия (2.3)'.

Исследование математической модели. Решение общей линейной аспределительной задачи, так же как и транспортной, как прави-о, разбивается на два этапа. На первом этапе находят какое-ни-удь решение, удовлетворяющее совокупности линейных равенств 2-1) и ограничениям (2.2), или убеждаются в том,-что такого ре-гения не существует. Этот этап называется отысканием опорного дана (базиса). На втором этапе производится последовательное-пучшение плана (базиса). В некоторых распределительных зада-

ах базис просматривается непосредственно, а во многих его необ-эдимо найти. "

В рассматриваемой задаче базис легко определяется. Для это-необходимо взять какие-либо т неизвестных, желательно, ная-лее редко встречающиеся в системе уравнений, и выразить их 4'ез остальные неизвестные. В нашей системе уравнений (т=3) -^5, xg, х7, которые и выражаем через оставшиеся неизвестные

• ^2, Хз, Х4. f Г

Полиномиальная интерполяция

Пусть на отрезке [х₀; х_n] заданы точки х₀,х₁,…,х_n (узлы интерполяции) и известны значения функции у = f(х) в этих точках: у₀ = f(х₀), у₁ = f(х₁),…, у_n = f(х_n). Требуется построить функцию φ(х), совпадающую в узлах интерполяции со значениями функции f(х).

Таблица значений функции f(х) может быть интерполирована бесконечным множеством различных функций, поэтому нужно иметь некоторый критерий выбора. Многие интерполирующие функции строятся как линейные комбинации элементарных функций. Линейные комбинации одночленов {х^R}₀ⁿ приводят к алгебраическим полиномам, линейные комбинации тригонометрических функций {cos Rx, sin Rx}₀ⁿ приводят к тригонометрическим полиномам.

Рассмотрим интерполяцию алгебраическими полиномами. В много-численных приложениях аппарата интерполяции в основном приходится решать две задачи:

1. найти аналитическое выражение для функции, заданной таблицей, графиком или в виде сложной для приложений формулы

2. вычислить значение функции f(х) в точках, не совпадающих с узлами интерполяции, с помощью сравнительно несложного алгоритма.

Интерполяционные полиномы находят также широкое применение в численном дифференцировании и интегрировании, при решении дифференциальных уравнений.

Интерполяционный полином Лагранжа. Выберем в качестве приближающей функции φ(х) полином Р_n(х) степени n, значения которого совпадают со значениями функции f(х) в узлах интерполяции, т. е.

Р_n(х₀) = у₀, Р_n(х₁) = у₁,…, Р_n(х_n) = у_n. (5.4)

Рис.11

Геометрически это задача о построении параболы n-го порядка у = P_n(х), пересекающейся с графиком функции у = f(х) в (n + 1)-й наперед заданной точке (рис.11). Покажем, что такая задача имеет единственное решение.

Пусть Р_n(х) = а₀ + а₁х + а₂х² + … + а_nхⁿ.

Коэффициенты а_i (i = 0, 1, 2,…, n) можно определить из системы уравнений

a₀ + a₁x₀ + a₂x₀² + … + a_nx₀ⁿ = y₀,

a₀ + a₁x₁ + a₂x₁² + … + a_nx₁ⁿ = y₁,

…………………………………. (5.5)

a₀ + a₁x_n + a₂x_n² + … + a_nx_nⁿ = y_n. .

Определитель этой системы

1 x₀ x₀² … x₀ⁿ

Δ = 1 x₁ x₁² … x₁ⁿ = Π (х_i – х_j)

……………… ^1≤j<i≤n

1 x_n x_n² … x_nⁿ

называется определителем Вандермонда. Если узлы интерполяции различны, то Δ ≠ 0, т. е. система (5.5) имеет единственное решение.

При определении полинома Р_n(х) используем базис так называемых лагранжевых коэффициентов L_i(х) (i = 0, 1,…, n) степени n таких, что

L_i(х_j) = 1, если i = j, (5.6)

0, если i ≠ j.

Определим L_i(х) как многочлен степени n, обращающийся в нуль в точках х₀, х₁,…, х_i–1, х_i+1,…, х_n и равный единице в точке х_i, полагая

L_i(х) = А(х – х₀)(х – х₁)…(х – х_i–1)(х – х_i+1)…(х – х_n).

При х = х_i

1 = А(х_i – х₀)(х_i – х₁)…(х_i – х_i–1)(х_i – х_i+1)…(х_i – х_n).

Определив значение А, получим окончательно

(x – x₀)(x – x₁)…(x – x_i–1)(x – x_i+1)…(x – x_n)

L_i(х) = ———————————————————— . (5.7)

(x_i – x₀)(x_i – x₁)…(x_i – x_i–1)(x_i – x_i+1)…(x_i – x_n)

Полином у_iL_i(х) принимает значение у_i в точке х_i и равен нулю во всех точках х_j (j ≠ i).

Обозначим ω_n(х) = (х – х₀)(х – х₁)…(х – х_n).

Легко убедиться в том, что ω^’_n(х_i) = (х_i – х₀)(х_i – х₁)…(х_i – х_i–1)(х_i – х_i+1)…(х_i – х_n).

ω_n(x)

Поэтому выражение (5.7) можно записать в виде L_i(х) = —————— .

(x – x_i)ω^’_n(x_i)

Лагранжевы коэффициенты L_i(х) называют еще множителями влияния соответствующих узлов интерполирования.

Интерполяционный полином Лагранжа степени n выражается формулой

_{n n} ω_n(x)

Р_n(х) = ∑ у_iL_i(х) = ∑ у_i —————— . (5.8)

^{i = 0 i = 0} (x – x_i)ω^’_n(x_i)

Число арифметических операций для его вычисления пропорционально n². Вычисление значений полинома Лагранжа для числа узлов n + 1 ≤ 9 осуществляется с помощью программы 11.

Отметим, что интерполяционный полином Лагранжа удобно применять в тех случаях, когда ведется многократное интерполирование по одним и тем же узлам (пусть даже для различных функций). Для этих узлов можно заранее составить коэффициенты Лагранжа L_i(х), поскольку они не зависят от функции f(х).

Однако, если для улучшения приближения потребуется повысить на единицу число узлов прибавлением нового узла, то полином Лагранжа придется перевычислить заново. В этом отношении удобней пользоваться интерполяцион-ным полиномом Ньютона (см. ниже).

Если не требуется находить общее выражение для полинома Лагранжа, а нужно только вычислять его значения для конкретных х, то удобно пользоваться интерполяционной схемой Эйткена [4].

Согласно этой схеме вычислим выражение

y₀ х₀ – х

у₁ х₁ – х

L₀₁(х) = —————— ,

х₁ – х₀

которое является линейным интерполяционным полиномом для узлов х₀ и х₁.

Для другой пары соседних узлов х₁ и х₂ вычислим аналогично

у₁ х₁ – х

у₁ х₂ – х

L₁₂(х) = —————

х₂ – х₁

и т.д.

Выражение

L₀₁(х) х₀ – х

L₁₂(х) х₂ – х

L₀₁₂(х) = ——————

х₂ – х₀

представляет собой квадратичный многочлен, интерполирующий значения у₀, у₁, у₂ соответственно в узлах х₀, х₁, х₂. Подключая последовательно новые узлы интерполяции, в общем случае получим выражение

L_{012…(n–1)}(х) х₀ – х

L_123…n(х) х_n – х

L_0123…n(х) = ———————— ,

х_n – х₀

которое будет интерполяционным многочленом Лагранжа, принимающим в точках х₀, х₁,…, х_n соответственно значения у₀, у₁,…, у_n. Вычисление значения этого полинома в точке х по схеме Эйткена удобно проводить, записывая промежуточные результаты в таблице 5.1 (для = 4).

Таблица 5.1

xi	yi	Li – 1, i	Li – 2, i – 1, i	Li –3, i – 2, i – 1, i	Li – 4, i – 3, i – 2, i – 1, i
x0 x1 x2 x3 x4	y0 y1 y2 y3 y4	L01 L12 L23 L34	L012 L123 L234	L0123 L1234	L01234

Описанный рекуррентный процесс интерполяции не требует априорного задания степени интерполяционного полинома. Новые узлы интерполяции подключаются в процессе вычислений, которые обычно проводятся до тех пор, пока последовательные значения L_0123…n(х) и L_012…n,n+!(х) не совпадут в пределах заданной точности. Вычисления элементов табл. 5.1 по схеме Эйткена реализуются на микрокалькуляторе с помощью программы 12.

Если узлы интерполяции равноудалены друг от друга, т. е. х_i+1 – x_i = h = const (i = 0, 1, 2,…,n – 1), то, введя переменную t = (х – х₀)/h, лагранжевы коэффициенты можно записать в виде

t(t – 1)(t – 2)…(t – n)

L_i(t) = ( – 1)^n–iC_nⁱ —————————, (5.9)

(t – i)n!

т. е. получить следующее выражение для интерполяционного полинома Лагранжа с равностоящими узлами

_n t(t – 1)(t – 2)…(t – n) _n С_nⁱ

Р_n(t) = ∑ у_iL_i(t) = ————————— ∑ ( – 1)^n–i —— у_i, (5.10)

^{i = 0} n! ^{i = 0} t – i

где коэффициенты L_i(t) не зависят от выбора шага h и от функции f(х). Для них составлены таблицы, упрощающие вычисление полинома Лагранжа.

Приведем оценку погрешности интерполяционного полинома Лагранжа [14]. Пусть функция f(х) имеет n + 1 непрерывную производную для всех х є [х₀; х_n]. Остаточный член интерполяционного полинома Лагранжа

f⁽ⁿ⁺¹⁾(ξ)

R_n(х) = f(х) – Р_n (х) = ———— ω_n(х), (5.11)

(n + 1)!

где ξ – внутренняя точка минимального отрезка, содержащего узлы интерполяции х₀, х₁,…, х_n и точку х. Погрешность зависит от выбора узлов х_i, точки х и свойств функции f(х). Известно [14], что величина sup│ω_n(х)│будет наименьшей, если в качестве узла интерполяции х є [а; b] выбрать корни полиномов Чебышева Т_n+1(х) = cos [(n + 1) arc cos х] для │х│≤ 1, определяемые по формулам

2i + 1

х_i = cos ——— π (i = 0, 1,…, n – 1).

2n + 2

Но такой выбор узлов редко применяется в практических задачах, поскольку при этом значительно усложнятся интерполяция, а выигрыш в точности невелик.

На значение интерполяционного многочлена в точке х наибольшее влияние оказывают ближайшие к точке х узлы интерполяции. Такие узлы обозначим через х₀ и х₁. Затем постепенно добавляем соседние узлы справа и слева, чтобы они симметрично располагались относительно точки х.

Погрешность интерполяции будет меньшей, если точка х расположена ближе к середине отрезка [х₀; х_n] [19] и может оказаться значительной, если проводить экстраполяцию, т. е. выбирать значения х вне отрезка [х₀; х_n].

Интерполяционный полином Ньютона. Укажем форму записи интерполяционного полинома Р_n(х), которая допускает уточнение результатов интерполяции последовательным прибавлением новых узлов. При этом будем использовать разделенные и конечные разности функции, являющиеся удобным аппаратом при работе с таблично заданными функциями.

Пусть для функции f(х) заданы не обязательно равноотстоящие узлы интерполяции х₀, х₁,…, х_n, х_i ≠ х_j при i ≠ j; у₀ = f(х₀), у₁ = (х₁),…, у_n = f(х_n) – соответствующие значения функции.

Разделенными разностями первого порядка называются величины, имеющие смысл средних скоростей изменения функции и вычисляемые по формулам:

f(х₁) – f(х₀) f(х_n) – f(х_n–1)

f(х₀; х₁) = ————— ,…, f(х_n–1; х_n) = —————— .

х₁ – х₀ х_n – х_n–1

Аналогично определяются разделенные разности второго порядка

f(х₁; х₂) – f(х₀; х₁)

f(х₀; х₁; х₂) = ———————— ,

х₂ – х₀

f(х₂; х₃) – f(х₁; х₂)

f(х₁; х₂; х₃) = ———————— .

х₃ – х₁

и т. д.

В общем случае разделенные разности R-го порядка определяются через разделенные разности (R – 1)-го порядка по рекуррентной формуле

f(х_i+1; х_i+2;…; (х_i+R) – f(х_i; х_i+1;…; х_i+R–1)

f(х_i; х_i+1;…; х_i+R) = ————————————————— ,

х_i+R – х_i

например,

f(х₁; х₂;…; х_n) – f(х₀; х₁;…; х_n–1)

f(х₀; х₁;…; х_n) = —————————————— .

х_n – х₀

Вычисления разделенных разностей удобно проводить в табл. 5.2 (n = 4).

Таблица 5.2

хi	f(xi)	Разделенные разности
		1-го порядка	2-го порядка	3-го порядка	4-го порядка
x0	ƒ(x0)
x1	f(x1)	ƒ(x0; x1)
x2	f(x2)	f(x1; x2)	ƒ(x0; x1; x2)
x3	f(x3)	f(x2; x3)	f(x1; x2; x3)	ƒ(x0; x1; x2; x3)
x4	f(x4)	f(x3; x4)	f(x2; x3; x4)	f(x1; x2; x3; x4)	ƒ(x0; x1; x2; x3; x4)

Отметим следующие основные свойства разделенных разностей [24].

1. Если функция f(х) n раз непрерывно дифференцируема, то выполняется соотношение

1

f(х₀; х₁;…; х_n) = — f⁽ⁿ⁾(ξ), где х₀ < ξ < х_n.

n!

2. Разделенные разности R-го порядка являются симметричными функциями своих аргументов и выражаются через узловые значения функции

_i+R f(х_j)

f(х_i; х_i+1;…; х_i+R) = ∑ ——— .

^j=i ω^’_R(х_j)

3. Разделенные разности n-го порядка от алгебраического многочлена n-ой степени постоянны, а разности более высоких порядков равны нулю.

Последнее свойство позволяет выбирать степень интерполяционного полинома такой, чтобы она совпадала с порядком практически постоянных разделенных разностей.

Интерполяционный полином может быть записан через разделенные разности в виде

P_n(x)=f(х₀)+(х–х₀)f(х₀;х₁)+(х–х₀)(х–х₁)f(х₀;х₁;х₂)+…+(х–х₀)(х–x₁)…(x–x_n1)f(x₀;x₁;…;x_n). (5.12)

Степень этого полинома не выше n. Кроме того, легко убедиться, что для такого полинома выполняются условия интерполяции (5.4). Полином, записанный в виде (5.12), называется интерполяционным полиномом Ньютона для не равноотстоящих узлов. Полиномы n-ой степени, определяемые формулами (5.8) и (5.12), тождественно равны, так как принимают равные значения в n + 1-ой точке и представляют собой различные формы записи одного и того же интерполяционного полинома.

Форма записи (5.12) удобна тем, что при добавлении к узлам х₀, х₁, …, х_n нового узла х_n+1 все вычисленные ранее члены остаются без изменения, а в (5.12) добавляется только одно слагаемое.

Отметим, что в (5.12) для вычисления полинома Ньютона используются разделенные разности, расположенные по верхней диагонали (в табл. 5.12 подчеркнуты). Если функция f(х) достаточно гладкая, а узлы интерполяции и точка х принадлежат малому отрезку, то слагаемые в (5.12) убывают. Поэтому на практике вычисления продолжают до тех пор, пока слагаемые остаются больше допустимой погрешности.

Если число узлов задано наперед, то значение полинома Ньютона удобнее вычислять по схеме Горнера, представив его в виде

P_n(x)=f(х₀)+(х–х₀)(f(х₀;х₁)+(х–х₁)(f(х₀;х₁;х₂)+… +(х–х_n–2)(f(х₀;х₁;…;х_n–1)+(х–х_n–1)f(x₀;x₁;…;x_n))…). (5.13)

Вычисления по этой формуле на микрокалькуляторе при n + 1 = 4 реализуются программой 15, а вычисления значений интерполяционного полинома Ньютона по формуле (5.12) для произвольного числа узлов по составленной таблице разделенных разностей реализуется на микрокалькуляторе с помощью программы 16.

Если в (5.12) положить n = 1, то получим часто используемую формулу линейной интерполяции

y₁ – у₀

Р₁(х) = у₀ + ——— (х – х₀). (5.14)

x₁ – х₀

Вычисления по этой формуле реализуются программой 13.

Запишем выражение для интерполяционного многочлена Ньютона в случае равностоящих узлов, если х_i+1 – х_i = h = const(i = 0, 1, …, n – 1). При этом будем использовать конечные разности для табличных значений функции

у_i = f(х_i) (i = 0, 1, …, n).

Конечные разности определяются рекуррентными формулами:

Δу_i = у_i+1 – у_i, Δ²у_i = Δ(Δу_i) = Δу_i+1 – Δу_i = у_i – 2у_i+1 + у_i=2, …, Δⁿу_i= Δ(Δ^n–!у_i) = =Δ^n–1у_i+1 – Δ^n–1у_i.

При вычислениях их удобно записывать в виде табл. 5.3 (n = 4).

Таблица 5.3

xi	yi	∆y	∆2y	∆3y	∆4y
x0 x1 x2 x3 x4	y0 y1 y2 y3 y4	∆y0 ∆ y1 ∆y2 ∆y3	∆2y0 ∆2y1 ∆2y2	∆3y0 ∆3y1	∆3y0

При х_i = х₀ + ih (i = 0, 1, …, n) выполняется соотношение между конечными и разделенными разностями [24]

Δⁿу₀

f(х₀; х₁;…; х_n) = —— .

n!hⁿ

Для интерполяции функции в точке х, близкой к х₀, введем новую переменную

х – х₀

t = ——— .

h

Тогда узлам интерполяции соответствуют значения t₀ = 0; t₁ = 1; …; t_n = n.

Множители в (5.12) преобразуются следующим образом:

х – х₀ х – х₁ х – х_n–!

——— = t , ——— = t – 1, …, ——— = t – n + 1.

h h h

На основании (5.12) получим формулу интерполяционного полинома Ньютона для интерполяции вперед:

t t(t – 1) t(t – 1)…(t – n + 1)

Р_n(t) = у₀ + — ∆у₀ + ——— ∆²у₀ + … + ———————— ∆ⁿу₀. (5.15)

1! 2! n!

Здесь используются конечные разности, расположенные на верхней диагонали в табл.5.3.

Для интерполяции функции в точке х, близкой к узлу х_n, удобнее ввести переменную:

x – x_n

t = ——— .

h

В этом случае получим формулу интерполяционного полинома Ньютона для интерполяции назад:

t t(t + 1) t(t + 1) … (t + n – 1)

Р_n(t) = у_n + — ∆у_n–1 + ——— ∆²у_n–2 + … + ————————— ∆ⁿу₀. (5.16)

1! 2! n!

В ней используются конечные разности, расположенные на нижней диагонали в табл. 5.3. Вычисление значений полинома Ньютона для равностоящих узлов по формулам (5.15) и (5.16) (число узлов n + 1  5) реализуется в автоматическом режиме программой 14.

Интерполяционный многочлен Эрмита. Рассмотрим теперь более общую задачу интерполирования, когда требуется, чтобы в узлах интерполяции совпадали не только значения искомой функции f(х) и интерполяционной функции Р(х), но и значения их производных вплоть до некоторого порядка. Если Р(х) – алгебраический многочлен n-oй степени, то его называют интерполяционным многочленом Эрмита и обозначают Н_n(х).

Многочлен Н_n(х) определяется из условий

Н_n(х₀) = f(х₀), Н^’_n(х₀) = f^’(х₀),…, Н_n^(a₀^–1) (х₀) = f^(a₀^–1) (х₀);

Н_n (х₁) = f(х₁), Н^’_n(х₁) = f^’(х₁),…, Н_n^(a₀^–1) (х₁) = f^(a₀^–1) (х₁);

………………………………………..

Н_n(х_s) = f(х_s), Н^’_n(х_s) = f^’(х_s),…, Н_n^(a₀^–1) (х_s) = f^(a_s^–1) (х_s). (5.17)

Если в узле x_R(R = 0, 1,…, s) полином и функция совпадают по производной порядка α_R – 1, то число α_R называется кратностью узла х_R. При этом α₁ + α₂ +…+ α_s = n + 1, где n – степень полинома.

Интерполяционная формула Ньютона (5.12) для неравных промежутков обобщается на случай кратных узлов [4]:

Н_n(х) = f(х₀) + (х – х₀)f(х₀; х₀) + (х – х₀)²f(х₀; х₀; х₀) +…+ (х – х₀)^a₀^–1f(х₀;…; х₀) + (х – х₀)^a₀ f(х₀;…; х₀; х₁) + (х – х₀)^a₀(х – х₁)f(х₀;…; х₀; х₁; х₁) +…+ (х – х₀)^a₀(х – х₁)^a₁…(х – х_s)^a_s^-1f(х₀;…; х₀;…; х_s;…; х_s). (5.18)

Разделенные разности в случае кратных узлов вычисляются по формулам:

f^(R–1)(х₀) 1

f(х₀;…; х₀) = ————,…, f(х₀;…; х₀; х₁;…; х₁;…; х_s;…; х_s) = ——— (f(х₀;…; х₀; х₁

(R – 1)! x_s – x₀

х₁;…; x_s;…; x_s) – f(х₀;…; х₀; х₁;…; х₁;…; х_s;…; х_s)). (5.19)

Выпишем общее выражение интерполяционного полинома Эрмита 4

_n ^α_i^{–1 α}_i^–1–1 1 1

Н_n(х) =∑ ∑ ∑ f^(j)(х_i) — — (х – х_i)^j+RΠ(х – х_m)^αr{d^R/dx^R Π(х – х_r)^–αr |_x=xi}.

^{i=0 j=0 R=0} R! J! ^{m≠i r≠i}

(5.20)

Формулы (5.18) и (5.20) в общем случае достаточно громоздки. Чем более высокие кратности узлов у полинома Эрмита заданной степени, тем меньше требуется брать узлов, что уменьшает вычислительную погрешность. На практике обычно выбирают немного узлов с небольшой кратностью. При этом легко составить таблицу разделенных разностей с кратными узлами. В первый столбец выписываются узлы интерполяции, причем каждый узел повторяется столько раз, какова его кратность. Во второй столбец выписываются соответствующие узлам значения функции. В третий столбец помещают разделенные разности 1-го порядка, если соответствующие аргументы не совпадают, или первые производные, если аргументы совпадают. В четвертый столбец помещает разделенные разности 2-го порядка, если они вычисляются так же, как обычные разделенные разности, или же производные второго порядка, деленные на 2!, если аргументы, на разность которых нужно делить, совпадают, и т. д. В частности, для двух узлов х₀ и х₁ кратности α₀ = 2 и α₁ = 2 получим табл. 5.4.

Таблица 5.4

xi	yi	Разделенные разности с кратными узлами
		1-го порядка	2-го порядка	3-го порядка
x0	y0
x0	y0	y0’
х1	y1	y1 – y0 ————— x1 – x0	y1 – y0 y0’ ————— - ————— (x1 – x0)2 x1 – x0
x1	y1	y0’	y1’ y1 – y0 ————— - ————— x1 – x0 (x1 – x0)2	y1’ + y0’ 2(y1 – y0) ————— - ————— (x1 – x0)2 (x1 – x0)3

Разности, стоящие по диагонали табл. 5.4, являются коэффициентами многочлена Н_n(х). Для указанного частного случая выпишем интерполяционный многочлен Эрмита

y₁ – y₀ y₀^’ y₁^’ – y₀^’

Н₃(х) = у₀ + (х – х₀)у₀ + (х – х₀)² ——— – ——— + (х – х₀)²(х – х₁) ——— –

(х₁ – х₀)² х₁ – х₀ (х₁ – х₀)²

2(у₁ – у₀)

– ———— . (5.21)

(х₁ – х₀)³

Для интерполяционного многочлена Эрмита оценка погрешности [4]

| f⁽ⁿ⁺¹⁾(ξ)|

|f(х) – Н_n(х)| = ———— |(х – х₀)^α0(х – х₁)^α1…(х – х_s)^αs|, (5.22)

(n + 1)!

Где ξ – внутренняя точка минимального отрезка, содержащего узлы интерполяции х₀, х₁,…, х_s и точку х. Отметим, что на одной и той же сетке узлов численная величина погрешности полинома Ньютона будет больше, чем у полинома Эрмита.

5.3. Лабораторная работа 5.

Полиномиальная интерполяция

Программа 11 вычисления интерполяционного полинома Лагранжа по формуле (5.8)

для числа узлов n + 1 ≤ 9 в автоматическом режиме:

Адрес	Команда	Код	Адрес	Команда	Код	Адрес	Команда	Код
00 01 02 03 04 05 06 07 08 09 10 11 12 13 14	ПД ПО ПС С/П ПА С/П КП ↑ FL0 05 0 ИПД ПО F, КИПС ПВ	4Г 40 4[ 50 4– 50 LЕ 5Г 05 00 6Г 40 25 Г[ 4L	15 16 17 18 19 20 21 22 23 24 25 26 27 28 29	F, С/П БП 22 ИПО ПС F, КИП ↑ ИПВ – FX≠0 37 ÷ КИП ↑ ИПА	25 50 51 22 60 4[ 25 ГЕ 6L 11 57 37 13 ГЕ 6–	30 31 32 33 34 35 36 37 38 39 40 41 42	–  FL0 22 + БП 10 F, FL0 19 + БП 10	11 12 5Г 22 10 51 10 25 5Г 19 10 51 10

Распределение регистров памяти:

Номер регистра	0	1, …, 9	А	В	С	Д
Переменная	счетчик цикла	xn, …, x0	x	xR	R	N + 1

Инструкция. 1. В режиме программирования (F ПРГ) ввести программу.

2. В режиме автоматической работы (F АВТ) вводить исходные данные и осуществлять вычисления по схеме: (n + 1) В/О С/П (х) С/П (х₀) С/П (х₁) С/П … (х_n) С/П (у₀) С/П (у₁) С/П … (у_n) С/П (каждое очередное число вводить после ОСТАНОВа). После последнего ОСТАНОВа списываем с индикатора значение Р_n(х).

При последующих ОСТАНОВах вводить последовательно значения узлов (х_i) С/П, значения конечных разностей (f(х₀; х₁;…; х_i)) (стоящих на верхней диагонали табл. 5.2) С/П, после ОСТАНОВа на индикаторе прочесть значение полинома Р_i(х).

Повторить п. 3 для каждого узла интерполяции, записывая, если нужно, значения полиномов Ньютона соответствующей степени в точке х.

Для новой таблицы значений функции повторить п. 2–4. Предполагается, что для значений функции составлена таблица разделенных разностей (см. табл. 5.2).

Контрольный пример. Для функции, заданной таблицей, вычислять значение пНьютона при х = 0,6:

xi	yi	Разделенные разности
0 0,2 0,5 0,7 1,0	1,0 1,2 1,6 2,0 2,7	1,00 1,33 2,00 2,33	0,66 1,34 0,66	0,97 –0,85	–1,82

После ввода программы заносим исходные данные: 0,6 П1 0 ПА В/О С/П; после ОСТАНОВа 1 С/П; после ОСТАНОВа 0,2 С/П, 1 С/П, прочтем на индикаторе значение Р₁(0,6) = 1,60; 0,5 С/П 0,66 С/П, прочтем значение Р₂(0,6) = 1,76; 0,7 С/П 0,97 С/П, прочтем значение Р₃(0,6) = 1,78; 1 С/П 1,82 ⁄ ⁄ С/П, прочтем значение Р₄(0,6) = 1,79 и т. д., при необходимости в процессе вычислений можно добавлять новые узлы интерполяции.

Задания к лабараторной работе 5. Для функции, заданной таблицей

xi	0	1,25	0,50	0,75	1,00
yi	1,00	1,28	1,65	2,12	2,72

вычислить значение полинома Лагранжа в точке х = 1 – 0,033n и полинома Ньютона в точке х = =0,033n (n = 1,…, 30 – номер варианта). Для вариантов 1–15 использовать формулу Ньютона интерполяции вперед (5.15), для вариантов 16–30 – формулу интерполяции назад (5.16).