1.3. Методы поиска экстремума унимодальных функций

Функция одной переменной, имеющая в интервале исследова­ния один горб (впадину), называется унимодальной, или: функция у—унимодальная, если х\<Хот (xi>Xoirr), х<2<Хот (л:2>^опт) я х,<х,,то Y(xi)<Y(x,)(Y(xi)>Y(x,)) [18].

Унимодальная функция не обязательно должна быть гладкой (рис. 1.3,а) и даже непрерывной (рис. 1.3,6) —она может быть из­ломанной (недифференцируемой), разрывной и даже может, в не­которых точках интервала быть неопределенной. Предположение унимодальности не связано с жесткими ограничениями и выпол­няется во многих практических задачах поиска оптимума. Преды­дущие методы нельзя применять к функциям с изломами и к раз­рывным функциям.

Если целевая функция унимодальна, то можно сузить интервал исследования функции на оптимум путем определения значений целевой функции в двух точках интервала задания функций Y(xi) и Y(xs) и последующего поинтервального сравнения. При этом воз­можны три случая (рис. 1.4);

1) если У1>У2, то Хопт<^2, т. е. оптимум не может лежать пра­вее, иначе нарушается предположение об унимодальности функции (интервал [хч, х\ из дальнейшего рассмотрения исключается);

2) если Yi<Ys, то Хопт>^1;

3) если У[===У2, то xi<Xoav<X2. . ' ^

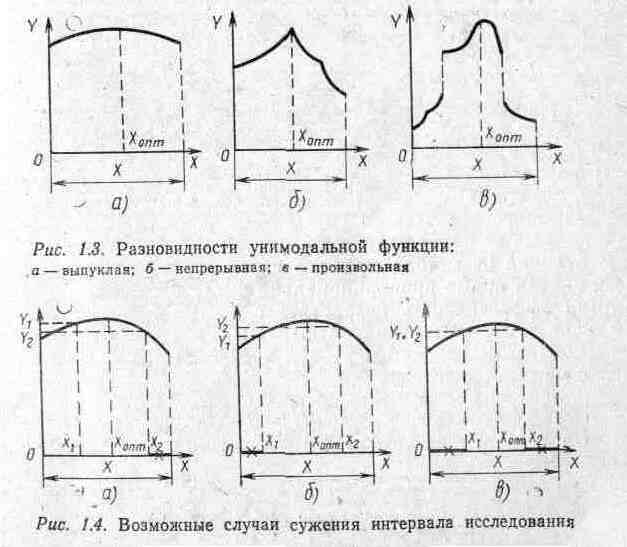
Как правило, задачи ис­следования операций имеют унимодальную целевую функцию.

Последовательно сужая интервал исследования, в котором находится оптимальное значение искомой управляющей переменной, можно с достаточной сте­пенью точности найти оптимальное значение искомой переменной. Для этого необходимо вы­работать такую стратегию поиска, чтобы за заданное число шагов (этапов) определить минимальный интервал, в котором лежит искомый оптимум, или свести исходный интервал до области за­данной длины за минимальное число шагов (расчетов).

К последовательным детерминированным методам поиска экс­тремума унимодальных функций (учитывающим результаты пре­дыдущих шагов) относятся методы дихотомии, Фибоначчи и золотого сечения.

Метод дихотомии (половинное деление). В этом методе-(рис. 1.5) искомая длина интервала исследования xn, в котором лежит искомый оптимум, уменьшается с каждом шагом N почти в два раза.

Алгоритм метода состоит из следующих этапов:

1) делят исходный интервал исследования пополам;

2) вблизи точки деления (по разные ее стороны) подсчитыва­ется дважды значение целевой функции y(x'n+\), Y(x"N+i)'.

x'N+i=XNl2—^xl2; ,xYn==W2+AA:/2,

где Дл;—наименьший интервал изменения управляющей перемен­ной, при котором становится возможным обнаружить отличие меж­ду Y(x'^} и Y(x"^);

3) используя свойство унимодальных функций, определяют ин­тервал, в котором находится экстремальное значение целевой функ­ции, затем процесс расчета повторяется по аналогичной схеме до тех пор, пока не будет найден Хот-

В отличие от метода прямого перебора, в котором эффектив­ность поиска прямо пропорциональна числу расчетов, в методе дихотомии эффективность возрастает с ростом N экспоненциально. Так, если для определения оптимального значения искомой пере­менной методом прямого перебора требуется около 1000 вычисле­ний, то методом дихотомии — 20. .

Интервал, в котором находится оптимум, после N шагов опре­деляется по формуле хн = [2-^N/²-{- (l--^-^²) &х]Ха, где Хо — первона­чальный интервал исследования; N—число шагов. Грубо говоря, Xo/XNw2^N/•^г. .

Метод Фибоначчи. Как ни эффективен метод дихотомии, существует еще более совершенный. В методе Фибоначчи точка делен! интервала исследования определяется с каждым новым расчета (в методе дихотомии необходимо на каждом шаге выполнять де расчета). В интервал исследования попадает предыдущий расчет, для продолжения поиска достаточно лишь произвести расчет симметрично имеющемуся.

'Пусть задано число расчетов (шагов) N. Необходимо их тг произвести, чтобы интервал, в котором лежит оптимум, был минимальным. Для этих целей наиболее подходят числа Фибоначчи

Fi{==Fif-i-}-Fi,r-2, Fv==Fi==l.

Алгоритм метода состоит из следующих этапов:

1) изменяют масштаб исходного интервала, в котором лежит оптимум. В качестве единицы измерения принимают l==XoJFif ш если задана длина интервала /, в котором лежит оптимум, наход) его на исходном интервале длиной хо. Для этого, разделив xq на находят близлежащее большее число Фибоначчи Fu, а по нек определяют N—число необходимых расчетов для определения интервала;

2) расставляют первые две точки x'i.vi х'\ на интервале исследования Хо на расстоянии Fif-2 от концов;

3) вычисляют значение целевой функции в этих точках для е жения интервала исследования. Пусть Y'i>Y"i, тогда интервал [х'\, Ек] исключаются из рассмотрения; 4) на новом интервале исследования снова расставляют с точки х'г и х"г, но в одной из них уже известно значение целевой функции У^//2==У^/l;

5) переходят к этапу 3 и так далее, пока не достигают искомого интервала, в котором лежит значение переменной, максимизирующее ее целевую функцию.

На рис. 1.6 видно, что интервал, в котором находится оптим сокращается до x'\=FN-\=Fs. Затем интервал, в котором находится оптимум, сократится до х"ч=х'\ при У^»^ и т. д. hocj ний N-w. расчет определяет интервал длиной /, в котором наход

;i экстремум целевой функции. Если при методе прямого счета ребуется около 1000 вычислений, то при методе дихотомии—20 : я методе Фибоначчи—15. Грубо говоря, '

Если сравнивать результаты расчета, полученные с помощью методов дихотомии и Фибоначчи, то легко заметить, что для поиска минимума в методе дихотомии потребовалось выполнить число итераций N=13 с двойным счетом, а при использовании метода Фибоначчи—только N==21 с одинарным на каждой итерации.

Метод золотого сечения. Метод Фибоначчи требует дополнительных расчетов, так как заранее неизвестно число предполагаемых вычислений. Однако существует еще один метод, который совершенно не зависит от числа готовящихся вычислений и почти так же эффективен, как метод Фибоначчи. Правило—каждый

I R^⁸^? ^точку P^⁴"'¹ симметрично на расстоянии, равном ',o^u,b2 от концов интервала исследования.

золотое сечение, как известно, проводит деление отрезка АВ на >й пяг^{авнь1ечасти} •"k, чтобы отношение всего отрезка АВ кболь-^ЙЛС' Р^иялось Отношению большей части СВ к мень-