Определение коэффициентов модели.

Введя фиктивную переменную х₀ = +1, уравнение простейшей 2^х факторной линейной модели удобно записывать в виде:

у=b₀ x₀+b₁ х₁+ b₂ x₂

С учетом значений фиктивной переменной матрица ПЭ 2² имеет вид:

№ опыта	Уровни переменных			Отклики Yu
	X0	X1	X2
1	+1	-1	-1	Y1
2	+1	+1	-1	Y2
3	+1	-1	+1	Y3
4	+1	+1	+1	Y4

Уровень модели содержит неизвестные коэффициенты b_і. Если все коэффициенты определяются по статистическим данням, то получаются не точные их значения, а статистические оценки, которые в математической статистике обозначаются малыми латинскими буквами (а,b, m …), в отличие от точных значений, обозначаемых малыми греческими буквами (,,,…).

Из-за случайностей величины у_uполучают не точные уравнения модели а его оценку:

(1)

Это уравнение называется моделью или уравнением регрессии, а функция У(x₁,… x_n) – поверхностью регрессии или (приі>2) гиперповерхностью регрессии.

Для отыскание оценок b_iприменяется метод наименьших квадратов (МНК), а сама процедура отыскания – регрессионным анализом. В задачах регрессионного анализа применяется обычно следующие принципиальные допущения: все независимые переменные, факторы x₁, x₂,… x_к задаются абсолютно точно и являются не случайными переменными.

Предполагается, что случайная величина у_uраспределена по нормальному закону, а дисперсии в отдельных точках факторного пространства однородны. При невыполнении этих условий необходимо применять спец. методы.

Среди суммируемых дисперсий нет таких, которое бы превосходили значительно все остальные.

Например, пусть даны результаты ПФЭ. Матрица двухфакторного эксперимента.

№ опыта	Уровни переменных			Отклики Yu
	X0	X1	X2
1	Х01	Х11	Х21	Y1
2	Х02	Х12	Х22	Y2
3	Х03	Х13	Х23	Y3
4	Х04	Х14	Х24	Y4

Требуется определить коэффициенты уравнения регрессии.

С геометрической точки зрения, задача заключается в проведении плоскости через 4 точки у₁, у₂, у₃, у₄.

Поскольку положение плоскости в трехмерном пространстве определяется 3_-мяточками не лежащими на одной прямой, то в данном случае необходимо дополнительное условие. Такое условие в МНК – требование минимума суммы квадратов отклонений точек от искомой точки.

В общем случае точки y_uне лежат на плоскости (1) и имеют невязки_u, которые определяются выражениями, где у_u– измеренное значение,- расчетное значение или_u = y_u-( b₀ x₀+b₁ х₁+ b₂ x₂), при u=1, 2, 3, 4. Число невязок_uравно числу опытов или строк в плане ПФЭ.

Значение коэффициентов b₀ ,b₁, b₂желательно выбирать так, что бы невязки по абсолютной величине были малы.

Положим e_u=0, тогда получим систему 4^хуравнений относительно трех неизвестных, которая является переопределенной и решения не имеет.

Согласно МНК сумма квадратов невязки e_uминимальна, если коэффициенты регрессии определены из условия:

, где - расчетное значение.

или в развернутом виде:

В данном случае задача отыскания коэффициентов сводиться к отысканию minфункции,(b_i) 3^хпеременныхb_0, b₁,b₂из условий:

или в развернутом виде:

Отсюда получаем систему начальных уравнений относительно b_0, b₁,b₂.

При ПЭ следует предусмотреть, чтобы определитель системы отличался от нуля.

Тогда вычислительная процедура упрощается.

Основное достоинство планов ПФЭ – простота определения коэффициентов регрессии, возможность учета произведений взаимодействия факторов без изменения плана основного эксперимента.

Преимущество любой матрицы ПФЭ достигается за счет особого построения плана эксперимента, при котором матрица обладает свойствами ортогональности, нормировки, симметрии и рототабельности.

Свойства ортогональности:сумма построчных элементов любых двух граф равна нулю.

где i,j– номер столбца или номер фактора;

і= 1, 2, …k(k– общее количество факторов);

u– номер набора факторов или номер строки;

N– общее число различных наборов или число строк матрицы ПФЭ.

Свойства нормировки – сумма квадратов элементов любой графы равна числу различных опытов – строк N,.

Свойство симметрии:алгебраическая сумма элементов любого реального фактора равна 0 (условие баланса положительных и отрицательных значений каждой переменной по столбцу)

Свойство рототабельности:дисперсии предсказанных значений отклика на равных расстояниях от центра плана постоянны и минимальны (т.е. инвариантны к вращению системы).

Используя свойства к системе ??? получаем, что в левых частях все суммы смешанных произведений обращаются в 0, каждая сумма квадратов факторов равна числу опытов N= 4. Так как х_0u=1по смыслу фиктивной переменной, система ??? принимает вид:

Отсюда

или в общем виде: 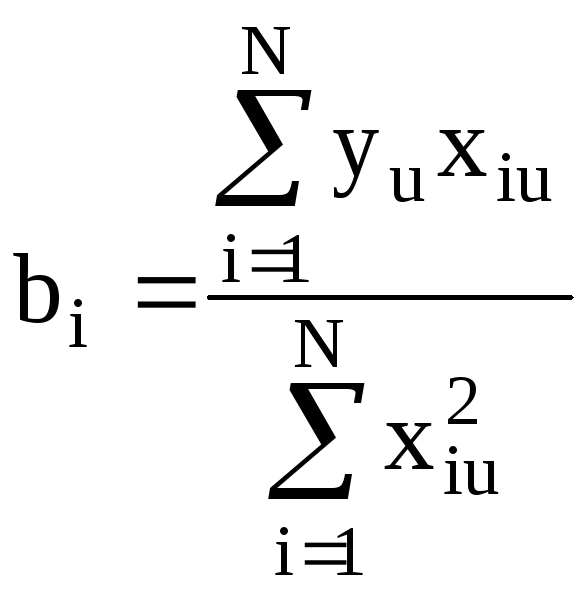, гдеi= 0, 1, …,k

При проведении 4 параллельных опытов в формулу вместо у_uподставляется их среднее значения